Золотое правило механики коэффициент полезного действия

Инфоурок
›
Физика
›Презентации›Презентация по физике на тему “Золотое правило. КПД” (7 класс)

Описание презентации по отдельным слайдам:
1 слайд

Описание слайда:
Давая выигрыш в силе или в пути, не дают ли простые механизмы выигрыша и в работе?
2 слайд

Описание слайда:
«Дайте мне точку опоры, и я подниму Землю!» Для подъёма Земли всего на 1 см длинное плечо рычага должно было бы описать дугу огромной длины. Для перемещения длинного конца рычага по этому пути, например со скоростью 1 м/с, потребовались бы миллионы лет
3 слайд

Описание слайда:
«Золотое правило» механики. Коэффициент полезного действия §60-61, Пример. С.151 Билет № 13
4 слайд

Описание слайда:
Действуя на длинное плечо рычага, мы выигрываем в силе, но при этом во столько же раз проигрываем в пути При использовании рычага выигрыша в работе не получают Не дает выигрыша в работе и неподвижный блок Пути, проходимые точками приложения сил F1 и F2, одинаковы, одинаковы и силы, а значит, одинаковы и работы
5 слайд

Описание слайда:
Получая выигрыш в силе в 2 раза, проигрывают в 2 раза в пути и подвижный блок не дает выигрыша в работе
6 слайд

Описание слайда:
Геро́н Александри́йский греческий математик и механик I в. до н.э. «Золотое правило» механики Ни один из простых механизмов выигрыша в работе не даёт!!! Во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии!!!
7 слайд

Описание слайда:
РАБОТА ПОЛЕЗНАЯ Ап ЗАТРАЧЕННАЯ Аз всегда < При равномерном подъеме (v=const) F=mg Aп=mgh При использовании простых механизмов дополнительная A (преодоление mg механизмов и Fтр)
8 слайд

Описание слайда:
Сборка экспериментальной установки Закрепите рейку трибометра в наклонном положении. Положите на рейку брусок, прикрепив к нему динамометр. Перемещайте брусок с постоянной скоростью вверх по наклонной плоскости.
9 слайд

Описание слайда:
Определение затраченной работы Измерить силу трения (Fтр= F.). Измерить длину наклонной плоскости (l). Рассчитать затраченную работу (Aз=Fтр·l).
10 слайд

Описание слайда:
Определение полезной работы Измерить вес бруска (Р). Измерить высоту наклонной плоскости (h). Рассчитать полезную работу (Aп = P · h).
11 слайд

Описание слайда:
Коэффициент полезного действия Какая доля Ап от Аз?
12 слайд

Описание слайда:
η – эта (греч.) Коэффициент полезного действия так как всегда Ап<Аз всегда КПД<100%
13 слайд

Описание слайда:
Если Fтр мало и массой простых механизмов можно пренебречь, то Ап≈Аз
14 слайд

Описание слайда:
«Золотое правило» механики Ни один из простых механизмов выигрыша в работе не даёт!!! Во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии!!! Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их вес Пример. С.151

Курс повышения квалификации

Курс профессиональной переподготовки
Учитель физики

Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Номер материала:
ДБ-071797
Вам будут интересны эти курсы:
Оставьте свой комментарий
Источник
Благодаря простым механизмам было сформулировано «золотое правило» механики. Оказалось, что все перемещения в простых механизмах имеют определенную связь с силами, которые развивает машина. Что же называют «золотым правилом механики»?

Простые механизмы
На протяжении многих столетий человек использует для совершения механической работы различные предметы и приспособления – простые механизмы. Различают следующие простые механизмы: рычаг, блок, ворот, винт, наклонная плоскость.
Рычаг представляет собой твердое тело, которое может вращаться вокруг неподвижной опоры. Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.
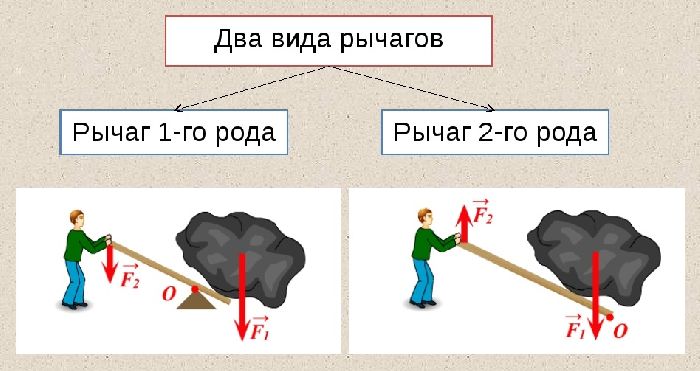
Рис. 1. Простые механизмы – рычаг.
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил: ${F1over F2}={l2over l1}$
А вот как сформулировал постулаты о рычаге сам Архимед:
1. Равные веса, находящиеся на равных расстояниях (от точки опоры), находятся в равновесии, а равные веса, находящиеся на неравных расстояниях, не находятся в равновесии, но перевес происходит в сторону того веса, который находится на большем расстоянии.
2. Если два веса, находясь на определенном расстоянии, уравновешивают друг друга и если к одному из этих весов что-нибудь прибавить, то веса уже не будут уравновешивать друг друга, но наклонятся к тому весу, который увеличили.
3. Если подобным же образом отнять что-либо от одного из весов, то весы не останутся в равновесии, но отклонятся к тому, от которого не отнимали.
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающий его по часовой стрелки, равен моменту силы, вращающему его против часовой стрелки.
Блок представляет собой колесо с желобом, которое укреплено в обойме.

Рис. 2. Простой механизм – блок.
Неподвижным блоком называют такой блок, ось которого закреплена и при подъеме грузов не поднимается и не опускается. Неподвижный блок можно рассматривать как равноплечный рычаг, у которого плечи сил равны радиусу колеса. Такой блок не дает выигрыша в силе, но позволяет менять направление действия силы.
У подвижного блока ось опускается и поднимается вместе с грузом, он позволяет получать выигрыш в силе.
«Золотое правило механики»
Перемещения, пройденные точками приложения сил на рычаге, обратно пропорциональны приложенным силам – это и есть «золотое правило» механики, которое можно выразить следующей формулой:
$ {S1over S2}= {F2over F1}$
Пользуясь правилом пропорции, получаем из последнего выражения равенство работ, совершенных плечами рычага:
$A1=S1*F1=A2=S2*F2$
Золотое правило механики гласит: не один механизм не дает выигрыша в работе. Во сколько раз мы выигрываем в силе во столько же раз мы проигрываем в расстоянии.

Рис. 3. Золотое правило механики формула.
Что мы узнали?
Простые механизмы известны со времен Архимеда. В данной статье даны определения таких механизмов, как рычаг и блок. Используя простые механизмы, выигрываем в одном, например в силе, зато проигрываем в другом – в расстоянии.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-
Александра Зебильян-Бездудная
5/5
Антон Савочкин
5/5
Ben Ten
5/5
Оценка доклада
Средняя оценка: 4. Всего получено оценок: 612.
Источник
Курс физики в общеобразовательных школах учителя начинают со знакомства с важным разделом этой науки — механики. Большой вклад в ее развитие внес Исаак Ньютон. Однако человечество знает других философов и ученых, которые имеют не менее важные заслуги. Хорошим примером в этом контексте является рассматриваемое в школах в 7 классе золотое правило механики.
Момент силы
Чтобы понять всю физическую суть золотого закона механики, необходимо познакомиться с таким важным понятием, как момент силы. Пусть существует некоторая система, которая состоит из следующих элементов:
Пусть к точке P перпендикулярно оси O приложена некоторая сила F. Тогда момент M этой силы будет равен:
M = [OP*F].
Квадратные скобки указывают на векторное произведение, поэтому величина M, являясь вектором, будет направлена вдоль оси O.
Момент силы измеряется в ньютонах на метр (Н*м) в системе СИ. Следует обратить внимание, что эти единицы соответствуют работе, измеряемой в джоулях (Дж). Этот факт не является случайным, поскольку произведение момента M на угол, на который поворачивается объект вокруг оси, является совершаемой силой F работой.
Введенная физическая величина не является исключительно теоретической, она имеет непосредственное практическое значение. Суть момента силы заключается в том, что он показывает возможность или способность силы совершить вращение в рассматриваемой системе. Например, если толкнуть дверь вблизи ручки, то открыть ее можно даже с помощью усилий одного мизинца. Наоборот, необходимо использовать силу всей руки, чтобы приоткрыть дверь, толкая ее вблизи навесных петель.
Простые механизмы
Человечество с древних времен использует подручные средства для облегчения физического труда. Простыми механизмами в современной науке принято называть такие объекты, которые позволяют преобразовывать величину и направление прилагаемых внешних усилий, при этом сами они не являются генераторами энергии. К этому классу механизмов относятся следующие:
- рычаг;
- блок;
- наклонная плоскость;
- ворот;
- клин;
- винт;
- колесо.
Некоторые физики продолжают спорить о минимальном количестве простых механизмов и о возможности представить одни из них, как комбинацию других. Каждый из них одновременно может преобразовывать направление приложенной силы и ее величину. Например, при закручивании гайки человек затрачивает незначительные усилия, выполняя отдельный виток. Эти усилия преобразуются, во-первых, в значительное создаваемое давление, во-вторых, его направление изменяется от перпендикулярного оси гайки или болта на параллельное ей.
Историческая справка
По общепризнанным представлениям простыми механизмами пользовались еще древние вавилоняне и египтяне во время создания своих сооружений из камня. Однако, до настоящего времени дошли в письменном виде лишь труды греческих античных философов касательно вопросов механики. Следует выделить две известные фамилии:
- Герон Александрийский;
- Архимед.
Именно эти два философа внесли основной вклад в развитие физической теории простых механизмов. Так, Архимед, живший в Греции в III веке до нашей эры, установил правило рычага. По одной из легенд он смог им воспользоваться на практике, когда в одиночку с помощью системы блоков и рычагов, которые он укрепил канатами, смог приподнять над поверхностью воды груженный пассажирами и товарами корабль.
Про Герона известно, что он жил в I веке нашей эры, то есть спустя 3 столетия после Архимеда, в египетском городе Александрии. Он известен, как величайший изобретатель в период расцвета эллинской культуры и науки.
Герон впервые с точки зрения математики рассмотрел все простые механизмы и обобщил полученные результаты в виде золотого правила механики.
Закон сохранения энергии
Золотое правило механики гласит: во время использования совершенно любого простого механизма во сколько раз осуществляется выигрыш в силе, во столько же раз происходит проигрыш в перемещении, и наоборот.
По этому определению можно смело утверждать, что оно является не чем иным, как законом сохранения энергии. Пусть имеется некий механизм, который способен в результате действия внешней силы F1, приложенной к произвольной точке O1, преобразовать эту силу в величину F2, которая уже будет приложена к точке O2. В процессе работы простого механизма обе точки переместятся на расстояния d1 и d2, соответственно. Тогда золотой закон может быть записан в следующей форме:
F1*d1 = F2*d2.
Произведение силы на путь дает работу. Таким образом, это равенство показывает сопоставимость работ, выполняемых двумя силами, то есть говорит о законе сохранения энергии.
Необходимо отметить, что рассмотренный пример справедлив для идеального механизма. В действительности все они являются реальными, для которых следует рассматривать потери на трение.
Иногда золотое правило в математическом виде можно сформулировать через другие физические величины. Для этого следует левую и правую части равенства разделить на время t продолжения действия сил. Тогда получаются еще два возможных выражения:
- F1*v1 = F2*v2;
- N1 = N2.
Здесь v1, v2 — скорости перемещения точек O1 и O2, соответственно. N1 и N2 — развиваемые силами F1 и F2 мощности.
Архимедов рычаг
Хорошей помощью в понимании золотого закона механики является презентация работы простого рычага. Он состоит из точки опоры и либо одного, либо двух плеч в зависимости от рода. Существуют три рода этого механизма:
Для рычагов всех родов справедлива следующая формула, которую получил еще Архимед:
F1*d1 = F2*d2.
Произведение силы на длину плеча является величиной постоянной. Следует обратить внимание, что сила должна быть приложена перпендикулярно плечу, если это условие не выполняется, то для справедливости равенства следует в него подставлять не сами силы, а их проекции на перпендикуляры к плечам.
Это выражение показывает равенство моментов. Действительно, согласно определению произведение F*d может рассматриваться как момент силы F. Золотое правило рычага в таком случае преобразуется в следующий вид:
M1 = M2.
Равенство моментов является одним из двух условий равновесия в системах, имеющих оси вращения. Второе условие — это равенство нулю всех действующих в системе сил. В случае рычага, который находится в равновесии, это условие может быть записано так:
F1 + F2 = N.
Где N — сила реакции опоры, вектор которой направлен в противоположную силам действия и противодействия сторону.
Пример задачи
Имеется рычаг первого рода. На какое расстояние необходимо положить груз массой 1 кг, чтобы он уравновесил шар, масса которого равна 10 кг и который находится на расстоянии 30 см от точки опоры.
Чтобы получить ответ на задачу, следует выполнить простой расчет согласно золотому правилу рычага:
F1*d1 = F2*d2 ==>
d1 = F2*d2/F1 = m2*g*d2/(m1*g) = m2*d2/m1.
Переводя расстояние d2 = 30 см в метры, и подставляя известные массы, можно получить ответ:
d1 = 10*0,3/1 = 3 метра.
Таким образом, золотой закон механики является универсальным. Его практическое изучение можно провести в лабораторных условиях на примере рычагов или обоймы блоков с желобами, используя при этом обычный динамометр и линейку.
Предыдущая
ФизикаСвободное падение тел – формулы, законы и задачи
Следующая
ФизикаПревращение энергии – виды, основные законы и примеры
Источник
Момент силы
Чтобы понять всю физическую суть золотого закона механики, необходимо познакомиться с таким важным понятием, как момент силы. Пусть существует некоторая система, которая состоит из следующих элементов:
- Оси вращения O.
- Материальной точки P, которая с помощью жесткого соединения связана с осью O. Расстояние от O до P является длиной отрезка OP.
Пусть к точке P перпендикулярно оси O приложена некоторая сила F. Тогда момент M этой силы будет равен:
M = [OP*F].
Квадратные скобки указывают на векторное произведение, поэтому величина M, являясь вектором, будет направлена вдоль оси O.
Момент силы измеряется в ньютонах на метр (Н*м) в системе СИ. Следует обратить внимание, что эти единицы соответствуют работе, измеряемой в джоулях (Дж). Этот факт не является случайным, поскольку произведение момента M на угол, на который поворачивается объект вокруг оси, является совершаемой силой F работой.
Введенная физическая величина не является исключительно теоретической, она имеет непосредственное практическое значение. Суть момента силы заключается в том, что он показывает возможность или способность силы совершить вращение в рассматриваемой системе. Например, если толкнуть дверь вблизи ручки, то открыть ее можно даже с помощью усилий одного мизинца. Наоборот, необходимо использовать силу всей руки, чтобы приоткрыть дверь, толкая ее вблизи навесных петель.
Простые механизмы
Человечество с древних времен использует подручные средства для облегчения физического труда. Простыми механизмами в современной науке принято называть такие объекты, которые позволяют преобразовывать величину и направление прилагаемых внешних усилий, при этом сами они не являются генераторами энергии. К этому классу механизмов относятся следующие:
- рычаг;
- блок;
- наклонная плоскость;
- ворот;
- клин;
- винт;
- колесо.
Некоторые физики продолжают спорить о минимальном количестве простых механизмов и о возможности представить одни из них, как комбинацию других. Каждый из них одновременно может преобразовывать направление приложенной силы и ее величину. Например, при закручивании гайки человек затрачивает незначительные усилия, выполняя отдельный виток. Эти усилия преобразуются, во-первых, в значительное создаваемое давление, во-вторых, его направление изменяется от перпендикулярного оси гайки или болта на параллельное ей.
Историческая справка
По общепризнанным представлениям простыми механизмами пользовались еще древние вавилоняне и египтяне во время создания своих сооружений из камня. Однако, до настоящего времени дошли в письменном виде лишь труды греческих античных философов касательно вопросов механики. Следует выделить две известные фамилии:
- Герон Александрийский;
- Архимед.
Именно эти два философа внесли основной вклад в развитие физической теории простых механизмов. Так, Архимед, живший в Греции в III веке до нашей эры, установил правило рычага. По одной из легенд он смог им воспользоваться на практике, когда в одиночку с помощью системы блоков и рычагов, которые он укрепил канатами, смог приподнять над поверхностью воды груженный пассажирами и товарами корабль.
Про Герона известно, что он жил в I веке нашей эры, то есть спустя 3 столетия после Архимеда, в египетском городе Александрии. Он известен, как величайший изобретатель в период расцвета эллинской культуры и науки.
Герон впервые с точки зрения математики рассмотрел все простые механизмы и обобщил полученные результаты в виде золотого правила механики.
Закон сохранения энергии
Золотое правило механики гласит: во время использования совершенно любого простого механизма во сколько раз осуществляется выигрыш в силе, во столько же раз происходит проигрыш в перемещении, и наоборот.
По этому определению можно смело утверждать, что оно является не чем иным, как законом сохранения энергии. Пусть имеется некий механизм, который способен в результате действия внешней силы F1, приложенной к произвольной точке O1, преобразовать эту силу в величину F2, которая уже будет приложена к точке O2. В процессе работы простого механизма обе точки переместятся на расстояния d1 и d2, соответственно. Тогда золотой закон может быть записан в следующей форме:
F1*d1 = F2*d2.
Произведение силы на путь дает работу. Таким образом, это равенство показывает сопоставимость работ, выполняемых двумя силами, то есть говорит о законе сохранения энергии.
Необходимо отметить, что рассмотренный пример справедлив для идеального механизма. В действительности все они являются реальными, для которых следует рассматривать потери на трение.
Иногда золотое правило в математическом виде можно сформулировать через другие физические величины. Для этого следует левую и правую части равенства разделить на время t продолжения действия сил. Тогда получаются еще два возможных выражения:
- F1*v1 = F2*v2;
- N1 = N2.
Здесь v1, v2 — скорости перемещения точек O1 и O2, соответственно. N1 и N2 — развиваемые силами F1 и F2 мощности.
Архимедов рычаг
Хорошей помощью в понимании золотого закона механики является презентация работы простого рычага. Он состоит из точки опоры и либо одного, либо двух плеч в зависимости от рода. Существуют три рода этого механизма:
- Точка приложения силы и точка сопротивления ей находятся по разные стороны от опоры. Такая конструкция позволяет с помощью действия меньшей по величине силы противодействовать значительным усилиям, хотя за счет проигрыша в пути. Примерами рычагов первого рода являются ножницы, плоскогубцы, катапульта, действие человеческих суставов и мышц.
- Внешняя сила и сопротивление действуют по одну сторону от опоры так, что плечо сопротивления всегда меньше плеча внешнего усилия. Это расположение действующих сил позволяет всегда выигрывать в силе и проигрывать в перемещении. Примерами механизмов-рычагов второго рода являются одноколесная ручная тачка и орехокол.
- Если внешняя сила и сопротивление приложены по одну сторону от опоры, но первая лежит ближе к ней, чем вторая, то ведут речь о рычаге третьего рода. Смысл его использования заключается в выигрыше. в перемещении, хотя для этого приходится пожертвовать прилагаемым усилием. Здесь можно привести такие примеры, как удочка для рыбной ловли и щипцы для ухода за бровями.
Для рычагов всех родов справедлива следующая формула, которую получил еще Архимед:
F1*d1 = F2*d2.
Произведение силы на длину плеча является величиной постоянной. Следует обратить внимание, что сила должна быть приложена перпендикулярно плечу, если это условие не выполняется, то для справедливости равенства следует в него подставлять не сами силы, а их проекции на перпендикуляры к плечам.
Это выражение показывает равенство моментов. Действительно, согласно определению произведение F*d может рассматриваться как момент силы F. Золотое правило рычага в таком случае преобразуется в следующий вид:
M1 = M2.
Равенство моментов является одним из двух условий равновесия в системах, имеющих оси вращения. Второе условие — это равенство нулю всех действующих в системе сил. В случае рычага, который находится в равновесии, это условие может быть записано так:
F1 + F2 = N.
Где N — сила реакции опоры, вектор которой направлен в противоположную силам действия и противодействия сторону.
Пример задачи
Имеется рычаг первого рода. На какое расстояние необходимо положить груз массой 1 кг, чтобы он уравновесил шар, масса которого равна 10 кг и который находится на расстоянии 30 см от точки опоры.
Чтобы получить ответ на задачу, следует выполнить простой расчет согласно золотому правилу рычага:
F1*d1 = F2*d2 ==>
d1 = F2*d2/F1 = m2*g*d2/(m1*g) = m2*d2/m1.
Переводя расстояние d2 = 30 см в метры, и подставляя известные массы, можно получить ответ:
d1 = 10*0,3/1 = 3 метра.
Таким образом, золотой закон механики является универсальным. Его практическое изучение можно провести в лабораторных условиях на примере рычагов или обоймы блоков с желобами, используя при этом обычный динамометр и линейку.
Источник
