Зависимость полезной мощности от внешнего сопротивления цепи график
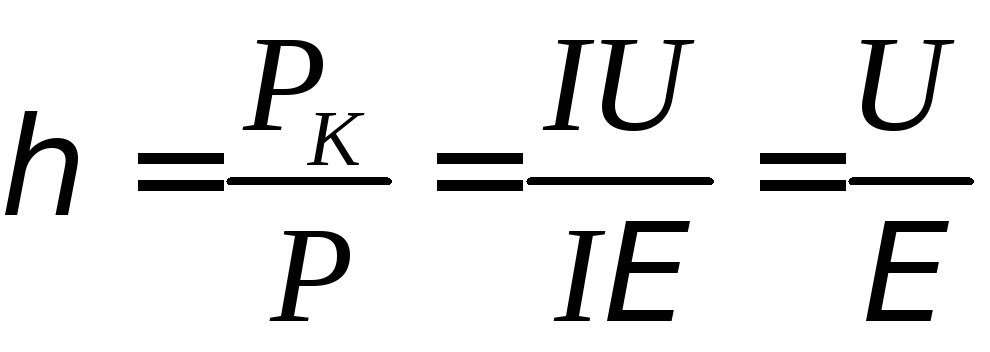
ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ:
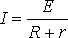 , (1)
, (1)
I- сила тока в цепи; Е- электродвижущая сила источника тока, включённого в цепь; R- сопротивление внешней цепи; r- внутреннее сопротивление источника тока.
МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО ВНЕШНЕЙ ЦЕПИ
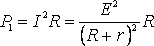 . (2)
. (2)
Из формулы (2) видно, что при коротком замыкании цепи (R®0) и при R®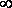 эта мощность равна нулю. При всех других конечных значениях Rмощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R0, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
эта мощность равна нулю. При всех других конечных значениях Rмощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R0, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
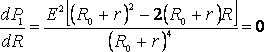 . (3)
. (3)
Из формулы (3), с учётом того, что R и r всегда положительны, а Е ? 0, после несложных алгебраических преобразований получим:
R0 = r. (4)
Следовательно, мощность, выделяемая во внешней цепи, достигает наибольшего значения при сопротивлении внешней цепи равном внутреннему сопротивлению источника тока.
При этом сила тока в цепи 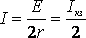 (5)
(5)
равна половине тока короткого замыкания. При этом мощность, выделяемая во внешней цепи, достигает своего максимального значения, равного
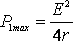 . (6)
. (6)
Когда источник замкнут на внешнее сопротивление, то ток протекает и внутри источника и при этом на внутреннем сопротивлении источника выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла равна
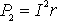 .
.  (7)
(7)
Следовательно, полная мощность, выделяемая во всей цепи , определится формулой
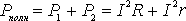 = I2(R+r) = IE (8)
= I2(R+r) = IE (8)
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ источника тока равен 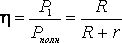 . (9)
. (9)
Из формулы (8) следует, что
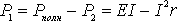 , (10)
, (10)
т.е. Р1 изменяется с изменением силы тока в цепи по параболическому закону и принимает нулевые значения при I = 0 и при 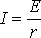 . Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид
. Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид
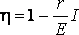 (11)
(11)
Таким образом, к.п.д. достигает наибольшего значения h =1 в случае разомкнутой цепи ( I = 0), а затем уменьшается по линейному закону, обращаясь в нуль при коротком замыкании.
Зависимость мощностей Р1, Рполн = EI и к.п.д. источника тока от силы тока в цепи показаны на рис.1.


Рис.1. I0 E/r
Из графиков видно, что получить одновременно полезную мощность и к.п.д. невозможно. Когда мощность, выделяемая на внешнем участке цепи Р1, достигает наибольшего значения, к.п.д. в этот момент равен 50%.
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ

Рис. 2.
Соберите на экране цепь, показанную на рис. 2. Для этого сначала щелкните левой кнопкой мыши над кнопкой  э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.
э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.
Разместите далее последовательно с источником резистор, изображающий его внутреннее сопротивление (нажав предварительно кнопку  в нижней части экрана) и амперметр (кнопка
в нижней части экрана) и амперметр (кнопка  там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр
там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр  , измеряющий напряжение на нагрузке.
, измеряющий напряжение на нагрузке.
Подключите соединительные провода. Для этого нажмите кнопку провода  внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.
внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.
4. Установите значения параметров для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой  . Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
. Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
Таблица 1. Исходные параметры электрической цепи
Номер варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Е, В | 10,0 | 9,5 | 9,0 | 8,5 | 8,0 | 8,5 | 9,0 | 9,5 |
r, Ом | 4,8 | 5,7 | 6,6 | 7,5 | 6,4 | 7,3 | 8,2 | 9,1 |
5. Установите сопротивление внешней цепи 2 Ом, нажмите кнопку «Счёт» и запишите показания электроизмерительных приборов в соответствующие строки таблицы 2.
6. Последовательно увеличивайте с помощью движка регулятора сопротивление внешней цепи на 0,5 Ом от 2 Ом до 20 Ом и, нажимая кнопку «Счёт», записывайте показания электроизмерительных приборов в таблицу 2.
7. Вычислите по формулам (2), (7), (8), (9) Р1, Р2, Рполн и h для каждой пары показаний вольтметра и амперметра и запишите рассчитанные значения в табл.2.
8. Постройте на одном листе миллиметровой бумаге графики зависимости P1 = f(R), P2 = f(R), Pполн=f(R), h = f (R) и U = f(R).
9. Рассчитайте погрешности измерений и сделайте выводы по результатам проведённых опытов.
Таблица 2. Результаты измерений и расчётов
R, Ом | 2,0 | 2,5 | 3,0 | … | 20 |
U, В | |||||
I, А | |||||
P1, Вт | |||||
P2, ВТ | |||||
Pполн, ВТ | |||||
h |
Вопросы и задания для самоконтроля
- Запишите закон Джоуля-Ленца в интегральной и дифференциальной формах.
- Что такое ток короткого замыкания?
- Что такое полная мощность?
- Как вычисляется к.п.д. источника тока?
- Докажите, что наибольшая полезная мощность выделяется при равенстве внешнего и внутреннего сопротивлений цепи.
- Верно ли утверждение, что мощность, выделяемая во внутренней части цепи, постоянна для данного источника?
- К зажимам батарейки карманного фонаря присоединили вольтметр, который показал 3,5 В.
- Затем вольтметр отсоединили и на его место подключили лампу, на цоколе которой было написано: Р=30 Вт, U=3,5 В. Лампа не горела.
- Объясните явление.
- При поочерёдном замыкании аккумулятора на сопротивления R1 и R2 в них за одно и то же время выделилось равное количество тепла. Определите внутреннее сопротивление аккумулятора.
Источник
Рассмотрим
электрическую цепь, состоящую из
источника постоянного тока и внешнего
сопротивления R
(рис. 1). При протекании тока через
такую цепь источником ЭДС выполняется
работа и в цепи выделяется мощность.
П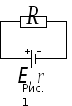 олезной
олезной
мощностью называют
мощность, которая выделяется на внешнем
сопротивлении. Из закона Джоуля-Ленца
(10*) полезная
мощность равняется
![]() ,
,
а из закона Ома для участка цепи![]() .
.
Тогда полезная мощность будет
| (1) |
где
![]() – падение напряжения на внешнем
– падение напряжения на внешнем
сопротивлении. При протекании тока по
цепи также выделяется „бесполезная”
мощность – разогревается источник ЭДС.
По закону Джоуля-Ленца эта мощность
равняется![]() .
.
Полная мощность, которая выделяется во
всей цепи, равняется![]() .
.
Используя закон Ома для полной цепи![]() ,
,
можно найти полную мощность
| (2) |
И так,
так,
полная мощность, которая выделяется в
цепи, равняется произведению силы тока
на ЭДС источника тока.
Пусть
в цепи можно менять внешнее сопротивление
![]() .
.
Проанализируем, как полезная и полная
мощности зависят от силы тока и внешнего
сопротивления.
Полезная
мощность
равняется разности между полной мощностью
и „бесполезной”:
| (3) |
![]()

Рис. 2
Из этого
выражения видно, что полезная мощность
является квадратичной функцией силы
тока I.
График этой функции будет представлять
собой параболу (рис. 2).
Из рис. 2
вытекает, что
![]() в двух случаях:
в двух случаях:
когда
цепь разомкнута (R = ∞),
то сила тока в цепи I = 0;когда
возникло короткое заключение, при этом
R = 0,
а сила тока в цепи будет максимальной
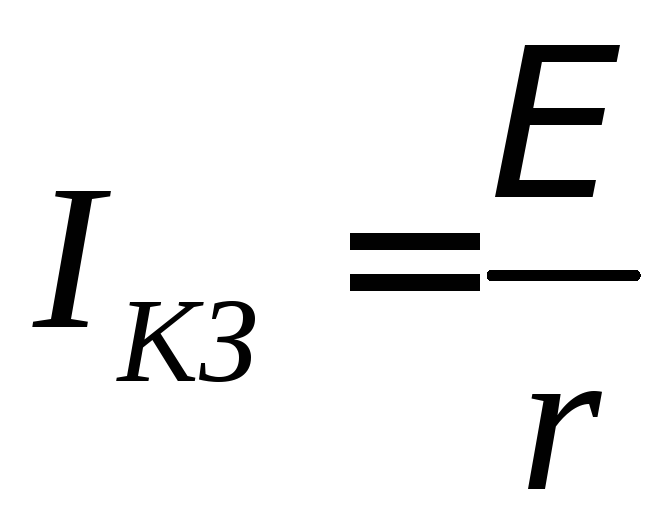 .
.
Меняя
величину внешнего сопротивления, можно
достичь некоторого значения силы тока
в цепи, при котором полезная мощность
будет максимальной. Найдем этот ток.
Для этого найдем первую производную
![]() и приравняем ее нулю. Из выражения (3)
и приравняем ее нулю. Из выражения (3)
имеем:
| (4) |
Отсюда
вытекает
| (5) |
а ток
![]() ,
,
при котором выделяется максимальная
полезная мощность, равняется![]() .
.
С другой стороны, на основании закона
Ома для полной цепи![]() ,
,
где![]() – сопротивление, при котором выделяется
– сопротивление, при котором выделяется
максимальная полезная мощность.
Приравнивая два последних выражения![]() ,
,
находим, что
| (6) |
Таким
образом, полезная
мощность будет максимальной при условии
равенства внешнего и внутреннего
сопротивлений.
Зависимость
полезной мощности от внешнего сопротивления
можно найти из закона
Джоуля-Ленца
![]() и закона Ома для полной цепи
и закона Ома для полной цепи![]()
| (7) |
График
зависимости
![]() показан на рис. 3 (криваяб).
показан на рис. 3 (криваяб).
Максимум функции
![]() можно найти, приравнивая
можно найти, приравнивая![]() нулю
нулю
| (8) |
Из
(8) также вытекает ожидаемое равенство
![]() .
.
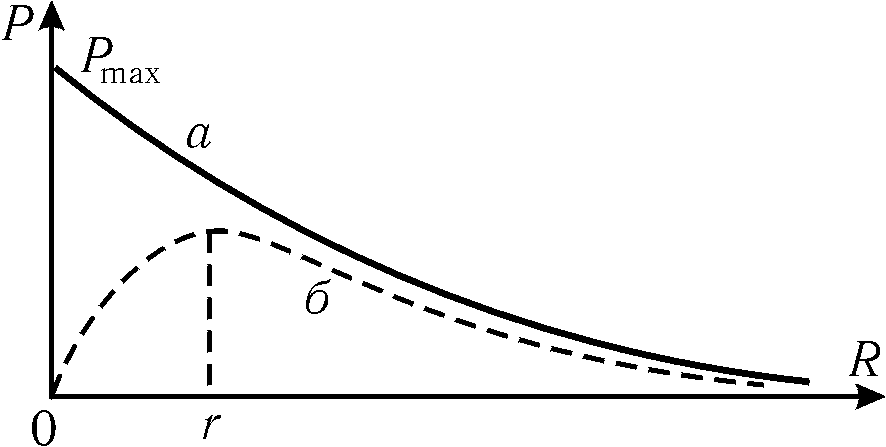

а
– полная мощность
б
– корисна потужність
Рис.
3
Рассмотрим
теперь, как полная мощность
зависит от внешнего сопротивления.
Используя выражение (2) и закон Ома для
полной цепи
![]() находим зависимость полной мощности
находим зависимость полной мощности
от внешнего сопротивления:
![]() .
.
(9)
График этой
зависимости показана на рис. 3 (кривая
а). При
изменении внешнего сопротивления от
нуля (короткое заключение) до бесконечности
(цепь разомкнута) полная мощность будет
убывать от максимального значения
![]() до нуля.
до нуля.
Зависимость
коэффициента полезного действия
источника электрического тока от силы
тока и внешнего сопротивления цепи
К оэффициент
оэффициент
полезного действия
(КПД) равняется отношению полезной
мощности (1) к полной мощности (2), которая
выделяется во всей цепи
| (10) |
С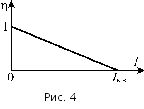 начала
начала
найдем зависимость КПД
от силы тока. Если
разделить выражение (3) для полезной
мощности на выражение (1) для полной
мощности, получим
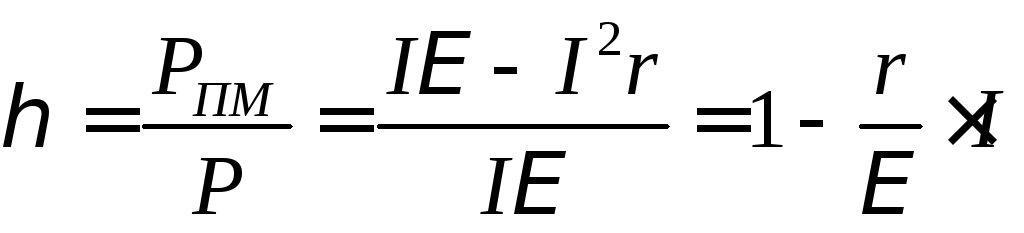
(11)
И так,
так,
КПД представляет собой линейную функцию
от силы тока (рис. 4). Когда I → 0
(цепь разомкнут), то
![]() .
.
При коротком заключении![]() ,
,
ток короткого заключения
| (12) |
и
КПД будет
![]() .
.
Чтобы найти
зависимость КПД от
внешнего сопротивления,
подставим в (9) выражение для
![]() из закона Ома для участки цепи
из закона Ома для участки цепи![]() ,
,
а выражение для![]() – из закона Ома для полной цепи
– из закона Ома для полной цепи![]() .
.
Тогда
| (13) |
Из соотношения (13)
вытекает:
при
R® 0
(короткое заключение,
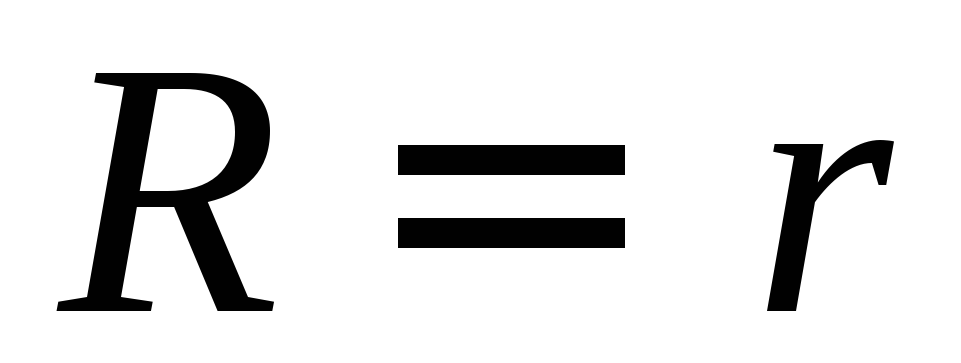 )
) ;
;при
R® ¥
( цепь разомкнут,
 )
) ;
;при
R = r
(условие максимума полезной мощности)
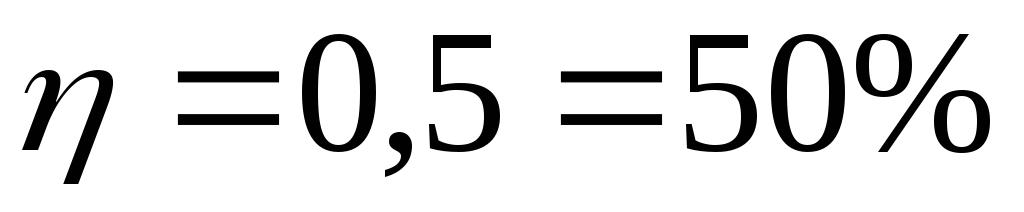 .
.
Приведенный
анализ показывает, что при увеличении
внешнего сопротивления КПД асимптотично
приближается к единице (рис. 5).
Соседние файлы в папке doc-формат
- #
- #
- #
- #
- #
- #
Источник
ЛАБОРАТОРНАЯ РАБОТА № 3.7.
ИССЛЕДОВАНИЕ ПОЛЕЗНОЙ МОЩНОСТИ И
КПД ИСТОЧНИКОВ ТОКА
Фамилия И.О. _____________ Группа ______ Дата
______
Введение
Цель данной работы –
экспериментально проверить теоретические выводы о зависимости полезной мощности
и КПД источника тока от сопротивления нагрузки.
Электрическая цепь состоит из
источника тока, подводящих проводов и нагрузки или потребителя тока. Каждый из
этих элементов цепи обладает сопротивлением.
Сопротивление подводящих проводов
обычно бывает очень мало, поэтому им можно пренебречь. В каждом участке цепи
будет расходоваться энергия источника тока. Весьма важное практическое значение
имеет вопрос о целесообразном расходовании электрической энергии.
Полная мощность Р, выделяемая в
цепи, будет слагаться из мощностей, выделяемых во внешней и внутренней частях
цепи: P = I2 ·R + I2·r = I2(R + r). Так
как I(R + r) = ε, то Р =I·ε,
где R
– внешнее сопротивление; r – внутреннее сопротивление; ε – ЭДС источника
тока.
Таким образом, полная мощность,
выделяемая в цепи, выражается произведением силы тока на ЭДС элемента. Эта
мощность выделяется за счет каких-либо сторонних источников энергии; такими
источниками энергии могут быть, например, химические процессы, происходящие в
элементе.
Рассмотрим, как зависит мощность,
выделяемая в цепи, от внешнего сопротивления R, на которое замкнут элемент.
Предположим, что элемент данной ЭДС и данного внутреннего сопротивления r
замыкается внешним сопротивлением R; определим зависимость от R полной мощности
Р, выделяемой в цепи, мощности Ра, выделяемой во внешней части цепи
и КПД.
Сила тока I в цепи выражается по
закону Ома соотношением
![]()
Полная мощность, выделяемая в
цепи, будет равна
![]()
При увеличении R мощность падает,
стремясь асимптотически к нулю при неограниченном увеличении R.
Мощность, выделяющаяся во внешней
части цепи, равна
![]()
Отсюда видно, что полезная
мощность Ра равна нулю в двух случаях – при R = 0 и R = ∞.
Исследуя функцию Ра
= f(R) на экстремум, получим, что Ра достигает максимума при R =
r, тогда
![]()
Чтобы убедится в том, что
максимум мощности Ра получается при R = r, возьмем производную Ра
по внешнему сопротивлению
![]()
Откуда
![]()
По условию максимума требуется
равенство нулю первой производной

![]() r2
r2
= R2
![]() R
R
= r
Можно убедиться, что при этом
условии мы получим максимум, а не минимум для Ра, определив знак
второй производной ![]() .
.
Коэффициент полезного действия
(КПД) η источника ЭДС это величина отношения мощности Ра,
выделяющейся во внешней цепи, к полной мощности Р, развиваемой источником ЭДС.
![]()
В сущности КПД источника ЭДС
указывает, какая доля работы сторонних сил преобразуется в электрическую
энергию и отдается во внешнюю цепь.
Выражая мощность через силу тока
I, разность потенциалов во внешней цепи U и величину электродвижущей силы
ε, получим
![]()
То есть КПД источника ЭДС равен
отношению напряжения во внешней цепи к ЭДС. В условиях применимости закона Ома
можно далее заменить U = IR; ε = I(R + r), тогда
![]()
Следовательно, в том случае,
когда вся энергия расходуется на Ленц-Джоулево тепло, КПД источника ЭДС равен отношению
внешнего сопротивления к полному сопротивлению цепи.
При R = 0 имеем η = 0. С
увеличением R, КПД возрастает, стремится к значению η=1 при неограниченном
увеличении R, однако при этом мощность, выделяющаяся во внешней цепи, стремится
к нулю. Таким образом, требования одновременного получения максимальной
полезной мощности при максимальном КПД невыполнимы.
Когда Ра достигает
максимума, то η = 50%. Когда же КПД η близок к единице, полезная
мощность мала по сравнению с максимальной мощностью, которую мог бы развивать
данный источник. Поэтому для увеличения КПД необходимо по возможности уменьшать
внутреннее сопротивление источника ЭДС, например, аккумулятора или
динамо-машины.
В случае R = 0 (короткое
замыкание) Ра = 0 и вся мощность выделяется внутри источника. Это
может привести к перегреву внутренних частей источника и выводу его из строя.
По этой причине короткие замыкания источников (динамо-машины, аккумуляторные
батареи) недопустимы!
На рис. 1 кривая 1
дает зависимость мощности Ра, выделяемой во внешней цепи, от
сопротивления внешней части цепи R; кривая 2 дает зависимость от R полной
мощности Р; кривая 3 – ход КПД η от того же внешнего сопротивления.
Порядок выполнения работы
1. Ознакомиться со схемой на стенде.
2. Установить с помощью магазина
сопротивление R = 100 Ом.
3. Замкнуть ключ К.
4. Произвести измерения силы тока в
цепи последовательно для различных девяти сопротивлений на магазине
сопротивлений, начиная от 100 Ом и выше. Внести в таблицу результаты измерений
силы тока, выразив их в амперах.
5. Выключить ключ К.
6. Вычислить для каждого
сопротивления Р, Ра (в ваттах) и η.
7. Построить графики Р, Ра
и η от R.
Контрольные вопросы
1. Что называется КПД источника ЭДС?
2. Вывести формулу КПД источника
ЭДС.
3. Что такое полезная мощность
источника ЭДС?
4. Вывести формулу полезной мощности
источника ЭДС.
5. Чему равна максимальная мощность,
выделяемая во внешней цепи (Ра)max?
6. При каком значении R полная
мощность Р, выделяющаяся в цепи, максимальна?
7. Чему равен КПД источника ЭДС при
(Ра)max?
8. Произвести исследование функции
(Ра) = f(R) на экстремум.
9. Зарисовать график зависимости Р,
Ра и η от внешнего сопротивления R.
10. Что такое ЭДС источника?
11. Почему сторонние силы должны быть
не электрического происхождения?
12. Почему недопустимо короткое
замыкание для источников напряжения?
№ п/п | R, Ом | I·10-3, |
|
|
|
1 | |||||
2 | 100 | ||||
3 | 200 | ||||
4 | 300 | ||||
5 | 400 | ||||
6 | 500 | ||||
7 | 600 | ||||
8 | 700 | ||||
9 | 800 | ||||
10 | 900 |
r = 300 Ом
Источник
Цель работы: экспериментальная проверка теоретических выводов о зависимости полезной мощности и КПД источника постоянного тока от сопротивления внешней нагрузки и силы тока в цепи.
Основные понятия и законы
Рассмотрим электрическую цепь, состоящую из источника тока и внешнего сопротивления (рисунок 9.2). Если замкнуть цепь, то падение потенциала распределится между внутренним и внешним участками цепи пропорционально их сопротивлениям:
, (9.1)
где – внутреннее сопротивление источника тока;
– сопротивление внешней цепи;
– ЭДС источника.
Из выражения (9.1) следует, что чем больше сопротивление внешней цепи, тем больше падение потенциала на нем. Показание вольтметра, присоединенного к полюсам источника, при разомкнутой цепи равно , так как при отсутствии внешней цепи сам вольтметр является нагрузкой. Если сопротивление вольтметра велико по сравнению с сопротивлением источника , то его показание будет приблизительно равно ЭДС источника:
= – Iri.
При переносе электрического заряда по проводнику между точками с потенциалами и совершается работа, равная:
. (9.2)
Мощность тока, измеряемая работой в единицу времени, будет равна:
. (9.3)
Из закона Ома для однородного участка цепи падение напряжения на участке цепи равно , где – сопротивление участка цепи. Подставляя выражение для в формулу мощности, получим:
. (9.4)
Полная мощность , выделяющаяся в замкнутой электрической цепи, равна сумме мощностей во внешней и внутренней части цепи, т.е.
(9.5)
или
= I . (9.6)
Полезной мощностью называется мощность, развиваемая на внешнем участке цепи. Она может быть найдена из уравнения:
. (9.7)
Из уравнения (9.7) следует, что полезная мощность , которую можно выразить произведением , является произведением двух сомножителей: и .
Полезная мощность может равняться нулю тогда, когда один из сомножителей равен нулю:
1) , т.е. при очень большом значении внешнего сопротивления
(R Þ ¥),
2) , когда внешнее сопротивление равно нулю R = 0 (короткое замыкание).
При некоторой силе тока, принимающей промежуточное значение между и максимальным значением силы тока , мощность во внешней цепи максимальна. Чтобы найти силу тока, при которой полезная мощность достигает наибольшего значения, нужно взять производную по от полезной мощности, выраженной формулой (9.7), и приравнять её к нулю:
.
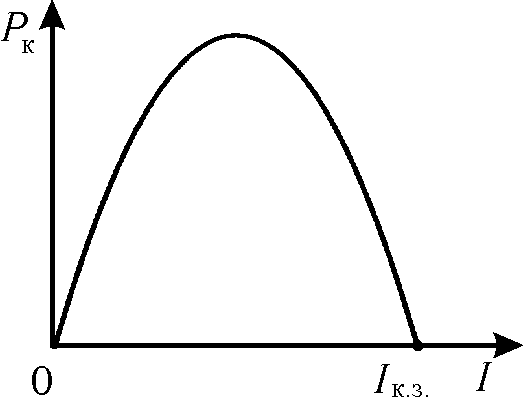
Получаем уравнение , откуда следует: . Это отношение имеет место в том случае, когда (см. уравнение (9.1)) внешнее сопротивление цепи будет равно внутреннему сопротивлению R =ri. График зависимости имеет вид параболы (рисунок 9.1), что следует из формулы (9.7).
Рисунок 9.1. – График зависимости полезной мощности от тока
Так как – ЭДС источника постоянна, то график зависимости полной мощности от тока представляет собой прямую, проходящую через начало координат:
.
Коэффициентом полезного действия источника тока называется отношение мощности , развиваемой на внешнем участке цепи, к полной мощности , развиваемой источником тока во всей цепи:
(9.8)
или
= . (9.9)
Формула (9.8) показывает, что КПД источника тока при постоянной ЭДС и постоянном внутреннем сопротивлении зависит только от силы тока , причём эта зависимость линейная, так как входит в формулу (9.8) в первой степени, и график зависимости выражается прямой линией. При силе тока, близкой к нулю, т.е. при очень большом сопротивлении внешней цепи, КПД источника тока имеет наибольшее значение , а минимальное значение, стремящееся к нулю, – при внешнем сопротивлении, равном нулю (короткое замыкание).
При. сопротивлении внешней цепи, равном внутреннему, , коэффициент полезного действия будет равен 0,5 (50 %), что соответствует максимальной полезной мощности.
Порядок выполнения работы
В данной работе необходимо исследовать зависимости полной мощности, полезной мощности и коэффициента полезного действия источника тока от силы тока и построить графики:
, , .
1. Для исследования указанных зависимостей необходимо собрать электрическую цепь по приведенной на рисунке 9.2 схеме.
Для искусственного увеличения внутреннего сопротивления источника тока (а значит ограничения тока при малом внешнем сопротивлении) внутри источника вмонтировано дополнительное сопротивление ri.
Максимум полезной мощности получается при равенстве сопротивления внешнего участка цепи и внутреннего , поэтому необходимо, чтобы и были сравнимы по порядку величины. Значение указывает преподаватель.
– источник постоянного тока, К – ключ, V – вольтметр, А – амперметр, – магазин сопротивлений, – вмонтированное внутри источника сопротивление (или магазин сопротивлений).
Рисунок 9.2. – Электрическая схема установки
2. При разомкнутом ключе К записать показание вольтметра. Это показание принять за ЭДС источника.
3. Замкнуть ключ К и установить на магазине такое сопротивление, чтобы ток был наибольшим. Показания амперметра и вольтметра записать.
4. С помощью магазина сопротивлений равномерно изменять ток от наибольшего до наименьшего значения таким образом, чтобы было по 5-6 значений тока и напряжения при сопротивлении внешней цепи и (всего 10–12 значений).
5. Разомкнуть ключ К и записать показание вольтметра .
6. Вычислить среднее значение ЭДС .
7. Вычислить для каждого значения силы тока полную и полезную мощность по формулам: , .
8. Вычислить коэффициент полезного действия по формуле: (выразить в процентах).
9. Заполнить таблицу 9.1.
Таблица 9.1
10. Построить графики зависимостей , , на одном рисунке. По оси абсцисс откладывать значения силы тока, по оси ординат – значения , , .
Указания. Для каждой величины , , выбрать соответствующий размерам рисунка масштаб, оставляя масштаб для неизменным.
9.3 Контрольные вопросы
1. Полезная и полная мощность цепи постоянного тока, её зависимость от силы тока, внешнего и внутреннего сопротивления. Закон Джоуля-Ленца.
2. Закон Ома для однородного и неоднородного участков цепи, закон Ома для полной цепи.
3. КПД источника тока, его зависимость от силы тока, внешнего и внутреннего сопротивления.
4. Что такое ток короткого замыкания?
5. При каких условиях выделяется максимум полезной мощности? Каково значение КПД при этих условиях?
Техника безопасности
1. Не включать схему без проверки преподавателем или лаборантом.
2. Во время работы запрещается касаться токоведущих частей установки.
3. По окончании работы отключить источник от сети и разобрать схему.
Источник

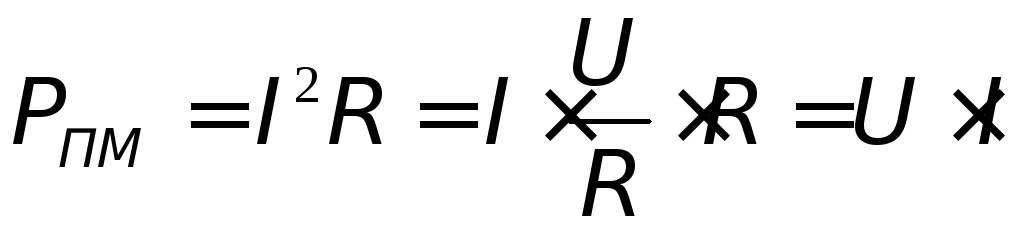 ,
,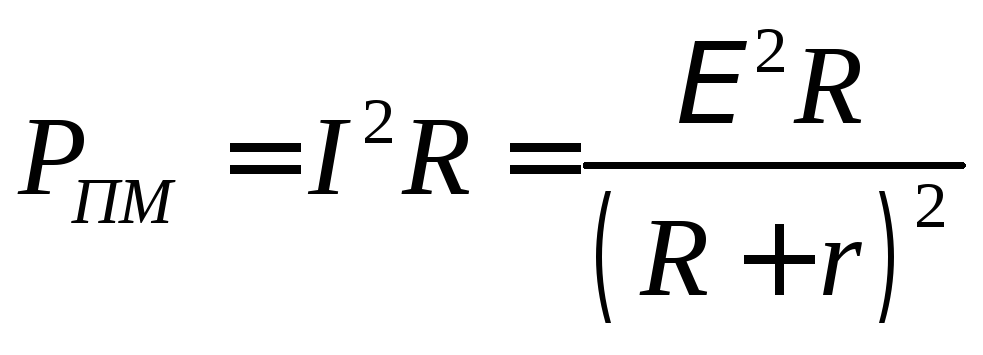 .
.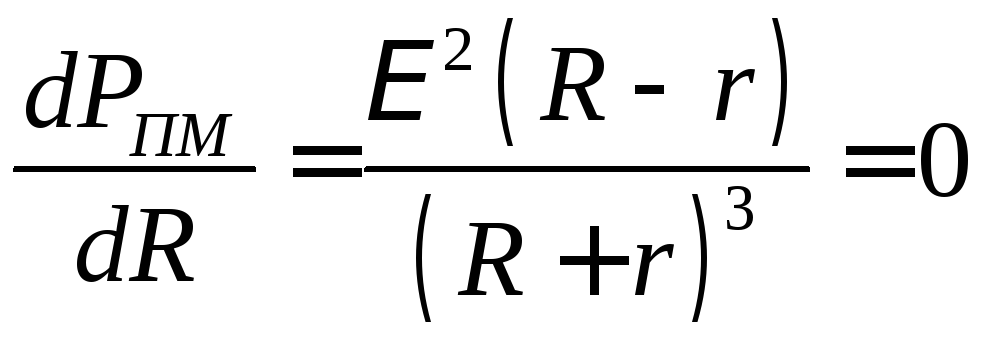 .
.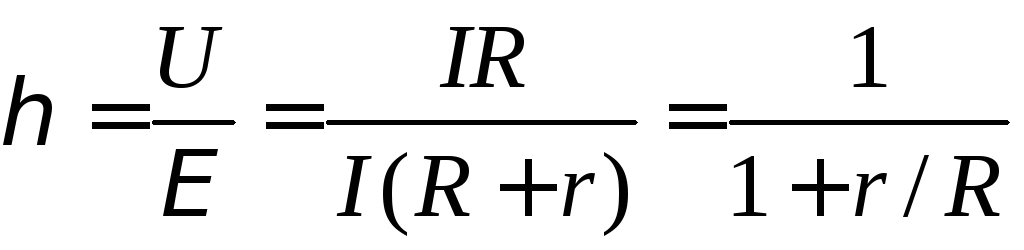 .
.