Задача по физике с коэффициентом полезного действия

У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.
Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.
Задачи по физике на КПД теплового двигателя
Задача на вычисление КПД теплового двигателя №1
Условие
Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.
Решение
Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:
Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:
Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.
Подставляем значения и вычисляем:
Ответ: 27%
Задача на вычисление КПД теплового двигателя №2
Условие
Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.
Решение
Найдем общее количество теплоты, которое произвел двигатель:
Теперь можно рассчитать КПД:
Или, умножая на 100, получаем значение КПД в процентах:
Ответ: 30%.
Задача на вычисление КПД теплового двигателя №3
Условие
Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.
Решение
КПД идеальной тепловой машины:
По условию:
Вычислим сначала работу, а затем КПД:
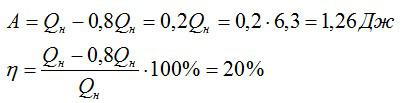
Ответ: 20%; 1,26 Дж.
Задача на вычисление КПД теплового двигателя №4
Условие
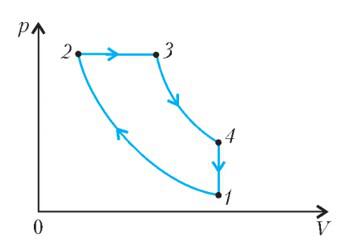
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.
Решение
Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.
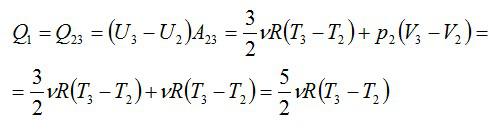
Аналогично:
Получим результат:
Ответ: См. выше.
Задача на вычисление КПД теплового двигателя №5
Условие
Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.
Решение
Запишем формулу для КПД:
Отсюда:
Ответ: 18%
Вопросы на тему тепловые двигатели
Вопрос 1. Что такое тепловой двигатель?
Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.
Вопрос 2. Приведите примеры тепловых двигателей.
Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:
- ракетный двигатель;
- авиационный двигатель;
- газовая турбина.
Вопрос 3. Может ли КПД двигателя быть равен единице?
Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.
КПД реальных двигателей редко превышает 30%.
Вопрос 4. Что такое КПД?
Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.
Вопрос 5. Что такое удельная теплота сгорания топлива?
Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.
Задачи и вопросы на цикл Карно
Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.
Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).
Задача на цикл Карно №1
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.
Решение
Рассчитаем КПД цикла:
С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:
Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:
Ответ: 0,36; 204,1 кДж; 130,6 кДж.
Задача на цикл Карно №2
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.
Решение
Формула для КПД цикла Карно:
Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:
Ответ: 17%.
Задача на цикл Карно №3
Условие
Изобразите цикл Карно на диаграмме и опишите его
Решение
Цикл Карно на диаграмме PV выглядит следующим образом:

- 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
- 2-3. Адиабатическое расширение, тепло не подводится;
- 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
- 4-1. Адиабатическое сжатие.
Ответ: см. выше.
Вопрос на цикл Карно №1
Сформулируйте первую теорему Карно
Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.
Вопрос на цикл Карно №2
Может ли коэффициент полезного действия в цикле Карно быть равным 100%?
Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.
Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.
Источник
Подробности
Просмотров: 669
«Физика – 10 класс»
Для решения задач надо воспользоваться известными выражениями для определения КПД тепловых машин и иметь в виду, что выражение (13.17) справедливо только для идеальной тепловой машины.
Задача 1.
В котле паровой машины температура 160 °С, а температура холодильника 10 °С.
Какую максимальную работу может теоретически совершить машина, если в топке, коэффициент полезного действия которой 60 %, сожжён уголь массой 200 кг с удельной теплотой сгорания 2,9 • 107 Дж/кг?
Р е ш е н и е.
Максимальную работу может совершить идеальная тепловая машина, работающая по циклу Карно, КПД которой η = (Т1 – Т2)/Т1, где Т1 и Т2 — абсолютные температуры нагревателя и холодильника. Для любой тепловой машины КПД определяется по формуле η = A/Q1, где А — работа, совершаемая тепловой машиной, Q1 — количество теплоты, полученной машиной от нагревателя.
Из условия задачи ясно, что Q1 — это часть количества теплоты, выделившейся при сгорании топлива: Q1 = η1mq.
Тогда откуда А = η1mq(1 – Т2/Т1) = 1,2 • 109 Дж.
Задача 2.
Паровая машина мощностью N = 14,7 кВт потребляет за 1 ч работы топливо массой m = 8,1 кг, с удельной теплотой сгорания q = 3,3 • 107 Дж/кг.
Температура котла 200 °С, холодильника 58 °С.
Определите КПД этой машины и сравните его с КПД идеальной тепловой машины.
Р е ш е н и е.
КПД тепловой машины равен отношению совершённой механической работы А к затраченному количеству теплоты Qlt выделяющейся при сгорании топлива.
Количество теплоты Q1 = mq.
Совершённая за это же время работа А = Nt.
Таким образом, η = A/Q1 = Nt/qm = 0,198, или η ≈ 20%.
Для идеальной тепловой машины η < ηид.
Задача 3.
Идеальная тепловая машина с КПД η работает по обратному циклу (рис. 13.15).

Какое максимальное количество теплоты можно забрать от холодильника, совершив механическую работу А?
Р е ш е н и е.
Поскольку холодильная машина работает по обратному циклу, то для перехода тепла от менее нагретого тела к более нагретому необходимо, чтобы внешние силы совершили положительную работу.
Принципиальная схема холодильной машины: от холодильника отбирается количество теплоты Q2, внешними силами совершается работа и нагревателю передаётся количество теплоты Q1.
Следовательно, Q2 = Q1(1 – η), Q1 = A/η.
Окончательно Q2 = (A/η)(1 – η).
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Основы термодинамики. Тепловые явления – Физика, учебник для 10 класса – Класс!ная физика
Насыщенный пар —
Давление насыщенного пара —
Влажность воздуха —
Примеры решения задач по теме «Насыщенный пар. Влажность воздуха» —
Кристаллические тела —
Аморфные тела —
Внутренняя энергия —
Работа в термодинамике —
Примеры решения задач по теме «Внутренняя энергия. Работа» —
Количество теплоты. Уравнение теплового баланса —
Примеры решения задач по теме: «Количество теплоты. Уравнение теплового баланса» —
Первый закон термодинамики —
Применение первого закона термодинамики к различным процессам —
Примеры решения задач по теме: «Первый закон термодинамики» —
Второй закон термодинамики —
Статистический характер второго закона термодинамики —
Принцип действия тепловых двигателей. Коэффициент полезного действия (КПД) тепловых двигателей —
Примеры решения задач по теме: «КПД тепловых двигателей»
Источник
1. Повторение формул и величин
Данный урок посвящён решению задач. Мы рассмотрим несколько задач на нахождение КПД тепловых установок. Кроме непосредственно КПД, в них фигурируют формулы для количества теплоты, необходимого для нагревания вещества или выделяемого при охлаждении, а также количества теплоты, которое выделяется при сгорании топлива.
Все эти вопросы мы уже рассматривали на прошлых уроках. Однако мы ещё не уделяли отдельное внимание задачам, в которых теплота сгорания топлива идёт на нагревание тел.
Поэтому на этом уроке мы подробно рассмотрим решение задач на нахождение КПД тепловых установок и двигателей. Как мы знаем, любая тепловая установка характеризуется своим КПД. Для нахождения КПД нам могут пригодиться следующие формулы:
– количество теплоты, которое выделяется при сгорании топлива ( – удельная теплота сгорания, – масса топлива);
– количество теплоты, которое выделяется при охлаждении или необходимо для нагревания вещества ( – удельная теплоёмкость вещества, – масса вещества, – конечная температура вещества, – начальная температура вещества);
– КПД установки ( – работа, совершённая рабочим телом, – количество теплоты, полученное от нагревателя);
Большинство из величин, встречающихся в формулах, либо даны в условии, либо являются искомыми. Однако удельная теплоёмкость вещества и удельная теплота сгорания берутся из соответствующих таблиц. Напомним единицы измерения этих величин: .
Кроме этих величин в задачах могут встречаться ещё две табличные величины: – удельная теплота парообразования, – удельная теплота плавления. Однако на этом уроке они нам не понадобятся, поэтому подробно останавливаться на них не будем.
Для удобства составим таблицу с теми значениями табличных величин, которые понадобятся на этом уроке при решении задач.
cellspacing=”0″>
Вещество | Удельная теплоёмкость | Удельная теплота сгорания |
Вода | – | |
Спирт | ||
Бензин |
2. Задача №1 на нахождение КПД
На спиртовке нагревают воду. Взяли воды и нагрели от до . При этом масса спиртовки уменьшилась с до . Найти КПД тепловой установки.
Решение
Запишем краткое условие задачи.
cellspacing=”0″>
Дано: | СИ | Решение: Вначале выпишем формулу для КПД: . В данном случае мы заменили работу полезным количеством теплоты, то есть тем количеством теплоты, которое пошло непосредственно на нагрев воды. |
Найти: |
Прежде чем решать задачу, необходимо определиться с процессами, которые происходят в данной задаче. Первый процесс – это сгорание топлива. Второй – нагревание воды.
Полезное количество теплоты, то есть то тепло, которое пошло непосредственно на нагревание воды, можно вычислить по формуле:
Количество теплоты, выделенное нагревателем, то есть, в данном случае, тепло, выделившееся при сгорании спирта:
Массу сгоревшего спирта найти легко: это та масса, на которую уменьшилась масса спиртовки, то есть: .
Получаем: .
Осталось вычислить КПД установки:
.
Заметим, что КПД может вычисляться не только в процентах, но и в долях. К примеру, для данной задачи ответ может быть: .
Если анализировать данную задачу, то можно увидеть, что только четвёртая часть (приблизительно) тепла, которое выделяется при сгорании спирта, идёт на нагревание воды. С одной стороны, это кажется достаточно малым значением, но, с другой стороны, для многих тепловых машин такое значение КПД оказывается даже большим.
Ответ:.
3. Задача №2 на нахождение КПД
Тепловой двигатель совершил полезную работу и израсходовал при этом бензина. Найти КПД теплового двигателя.
Решение
Запишем краткое условие задачи.
cellspacing=”0″>
Дано: | СИ | Решение: Вначале выпишем формулу для КПД: . По таблице находим, что: . Для того чтобы найти КПД, достаточно найти . |
Найти: |
Как и в прошлой задаче, воспользуемся следующей формулой: .
Находим КПД:
.
Ответ:.
Итак, мы решили несколько задач на нахождение КПД тепловых двигателей и установок, вспомнили основные формулы и величины, которые требуются для решения таких задач.
На следующем уроке мы рассмотрим более сложные задачи, которые могут встретиться в теме «Тепловые явления».
Вопросы к конспектам
Каков КПД теплового двигателя, который совершил полезную работу , если при полном сгорании топлива выделилась бы энергия ?
Израсходовав бензина, тепловой двигатель совершил полезную работу . Каков КПД этого двигателя?
Сколько природного газа необходимо сжечь для совершения полезной работы , если КПД двигателя ?
Источник
Теория
| 1. | Коэффициент полезного действия механизма |
Задания
| 1. | КПД рычага Сложность: | 1 |
| 2. | КПД неподвижных блоков Сложность: | 1 |
| 3. | Работа, производимая для поднятия груза Сложность: | 2 |
| 4. | КПД экскаватора Сложность: | 2 |
| 5. | КПД подъёмника Сложность: | 2 |
| 6. | КПД механизма для забивания свай Сложность: | 2 |
| 7. | Работа по преодолению силы трения и КПД Сложность: | 3 |
| 8. | Полезная работа Сложность: | 3 |
| 9. | КПД, наклонная плоскость Сложность: | 3 |
| 10. | Сила тяги моторов Сложность: | 4 |
| 11. | КПД установки Сложность: | 3 |
| 12. | Масса воды Сложность: | 4 |
| 13. | Скорость поезда Сложность: | 4 |
| 14. | Подвижный блок Сложность: | 4 |
Тесты
| 1. | Тренировка по теме «Коэффициент полезного действия» Сложность: среднее | 8 |
Методические материалы
| 1. | Технологическая карта |
Источник
