Задача на полезную и совершенную работу
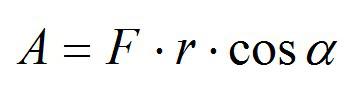
§ 1 Повторение формул по теме урока
В этом уроке мы рассмотрим решение задач на расчет механической работы и мощности, коэффициент полезного действия простых механизмов.
Для решения задач нужно знать формулы:
· Механическая работа равна произведению модуля силы на пройденный путь: A = F · s. Мощность равна отношению работы ко времени ее выполнения: N = A / t.
· Потенциальная энергия тела, поднятого над землей, вычисляется по формуле:
Еп = mgh.
· Кинетическая энергия – это энергия движения тела, зависит от скорости движения и массы тела: Ек = m υ2/2.
· Коэффициент полезного действия равен отношению полезной работы ко всей полной совершенной работе: η = Апоез/ Аполн.
· Простые механизмы, используемые для выполнения работы, позволяют получить выигрыш в силе, например, подвижный блок дает выигрыш в силе в 2 раза: Pгруза = 2 · Fприл, но при этом проигрываем в пути также в 2 раза.
§ 2 Решение задач
С помощью рычага груз массой 100 кг был поднят равномерно на высоту 80 см. При этом длинное плечо рычага, к которому приложена сила 600 Н, опустилось на 2 м. Определите коэффициент полезного действия рычага.
Запишем условие задачи: масса груза m = 100 кг, сила F = 600 Н, путь, пройденный грузом s1 = h = 80 см = 0,8 м, путь, пройденный длинным плечом рычага s2 = 2 м. Найти кпд η.
Решение: Чтобы найти кпд, определим полезную и полную работу. Полезная работа – это работа по поднятию груза весом mgна 80 см: Аполез = P · s1 = mgh = 100 кг · 10Н/кг · 0,8 м = 800 Дж. Полная работа – это работа, совершенная силой, приложенной к длинному плечу рычага, Аполн = F · s2 = 600 Н · 2 м = 1200 Дж.
Тогда кпд механизма равен: η = Аполез/ Аполн = 800 Дж / 1200 Дж = 0, 67 = 67%

Какая сила потребуется для равномерного поднятия груза массой 200 кг по наклонной плоскости, имеющей кпд 60%? Высота наклонной плоскости –1,5 м, длина – 10 м.
Запишем условие задачи: масса m = 200 кг, высота наклонной плоскости h= 1,5 м, длина l = 10 м, кпд установки η = 60% = 0,6 в системе СИ. Найти приложенную силу F.
Решение: При помощи наклонной плоскости поднимают груз, то есть совершают работу. Полезная работа равна произведению веса груза mg на высоту h. Полная работа совершается приложенной силой на пути, равном длине наклонной плоскости: Аполн = F · s2 = F · l.
Подставим записанные формулы в формулу коэффициента полезного действия и выразим неизвестную величину – приложенную силу: F равно mgh делим на кпд и l. Вычислим, подставив числовые значения известных величин. Ответ: для подъема груза требуется сила 500 Н.

Водяной насос подает 300 л воды в минуту на высоту 20 м. Определить мощность двигателя насоса, если его кпд равен 80%.
Запишем условие задачи: объем воды V = 300 л = 0,3 м3, время работы t = 1 мин = 60 с, путь, пройденный водой, равен высоте s1 = h = 20 м, плотность воды ρ = 1000 кг/м3, кпд насоса η = 80% = 0,8. Найти мощность двигателя N.
Решение: При помощи насоса совершают работу по поднятию воды. Полезная работа равна произведению веса воды на высоту: Аполез = P · s1 = mgh, массу воды найдем по формуле плотности m = ρ · V = 1000 кг/м3 · 0,3 м3 = 300 кг. Тогда полезная работа составит 60 000 Дж.
Полную работу, совершенную двигателем насоса, можно найти по формуле мощности: Аполн = N · t. Подставим в формулу кпд формулу полной работы и выразим неизвестную мощность: N= Аполез/ кпд и время. Вычислим. Ответ: мощность двигателя насоса 1250 Вт.

Итак, при решении задач на расчет коэффициента полезного действия нужно правильно определить, что является полезной работой и что является полной работой. Для этого можно поставить вопрос: с какой целью применяют тот или иной механизм? Ответ на него позволяет определить полезную работу. Полной работой является работа, совершенная самим механизмом.
§ 3 Важно запоминить
Коэффициент полезного действия – это величина, показывающая долю полезной работы от всей полной совершенной работы. КПД выражают в процентах. При решении задач на расчет коэффициента полезного действия нужно определить полезную работу и полную совершенную работу. КПД механизмов всегда меньше 100%.
Источник
В сегодняшней статье кратко расскажем про работу и мощность в механике, а также приведем примеры задач для тех, кто учится их решать.
Больше полезной информации для студентов всех специальностей — на нашем телеграм-канале. Подписывайтесь!
Задачи на механическую работу и мощность с решениями
Задача №1. Нахождение механической работы
Условие
Грузчик равномерно толкает ящик с осциллографами по горизонтальному полу. Сила трения равна 450 Н. Найдите работу, совершенную грузчиком, если ящик передвинули на 20 метров.
Решение
Так как ящик двигался равномерно, то сила тяги грузчика равна силе трения.
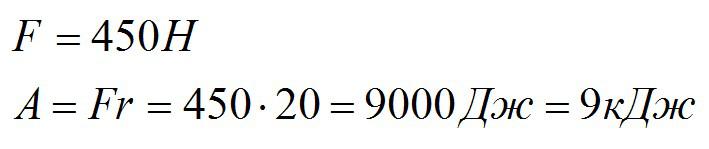
Ответ: 9кДж
Задача №2. Расчет работы силы тяжести
Условие
Гантель массой 1 кг падает с высоты 10 метров. Какую работу совершает сила тяжести?
Решение
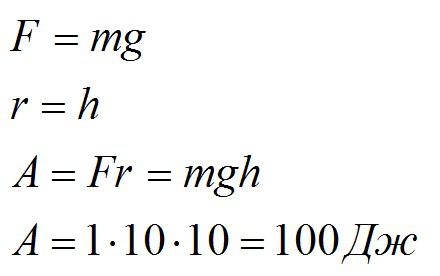
Ответ: 100 Дж.
mgh – выражение для потенциальной энергии камня в наивысшей точке.
Задача №3. Расчет механической мощности и работы
Условие
Деревенский житель поднимает ведро из колодца за 20 секунд, действуя с постоянной силой 80 Н. Глубина колодца равна h=10 м. Какую мощность развивает человек?
Решение
Сначала найдем работу, совершаемую при подъеме ведра, а затем вычислим мощность:
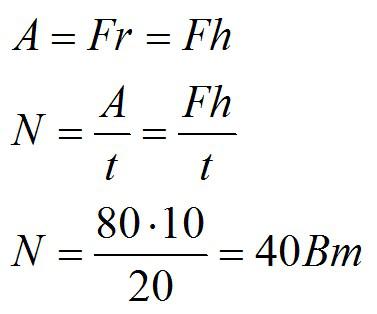
Ответ: 40 Вт.
Задача №4. Нахождение мощности. Связь мощности, силы и скорости
Условие
Мотороллер движется со скоростью 60 км/ч. Сила тяги двигателя равна 245 Н. Какую мощность развивает двигатель?
Решение
Переведем значение скорости в систему СИ и применим формулу, связывающую мощность, силу и скорость: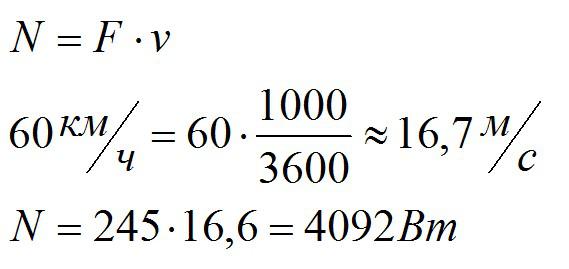
Ответ: 4092 Вт.
Задача №5. Нахождение механической работы.
Условие
Мощность двигателя трамвая равна 86 кВт. Какую работу может совершить трамвай за 2 часа непрерывной езды?
Решение
Работу можно вычислить из определения мощности:
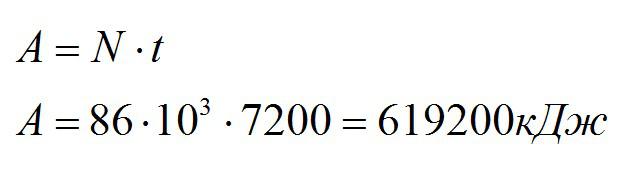
Ответ: 619200 кДж
Вопросы на механическую мощность и работу
Вопрос 1. Сила тяжести действует на автомобиль, едущий по прямой и горизонтальной дороге. Совершает ли эта сила работу?
Ответ. Не совершает. Работу в данном случае совершает сила тяги двигателя автомобиля.
Вопрос 2. Приведите примеры механической работы.
Ответ. Примеры в которых совершается механическая работа:
- лошадь тянет телегу (работу совершает сила тяги лошади);
- бурлаки на Волге тянут баржу (работу совершает мускульная сила рук бурлаков);
- спортсмен поднимает штангу (работу совершает мускульная сила рук спортсмена).
Вопрос 3. Камень падает с неба. Совершает ли сила тяжести работу?
Ответ. Да, совершает. Это работа так называемых потенциальных, или диссипативных, сил.
Вопрос 4. Какие есть внесистемные единицы измерения мощности?
Ответ. Самая распространенная внесистемная единица измерения мощности – лошадиная сила.
1 лошадиная сила равна примерно 745 Ваттам.
Вопрос 5. Какая еще величина выражается в Джоулях?
Ответ. Джоуль — единица измерения не только работы, но и энергии.
Работа и мощность в механике
Работа в механике
Для работы существует множество определений. Нас в данном случае интересует лишь одно:
Механическая работа – скалярная физическая величина, равная произведению силы, действующей на тело, на модуль перемещения, которое совершает тело под действием этой силы.
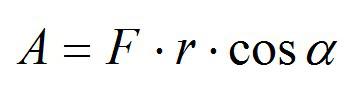
Если направления векторов силы и перемещения не совпадают, в определение добавляется третий множитель: косинус угла альфа между векторами.
Единица измерения работы: Джоуль
Мощность в механике
Мощность показывает, какая работа совершается за единицу времени.
Механическая мощность – скалярная физическая величина, равная отношению работы ко времени, за которое она совершалась.
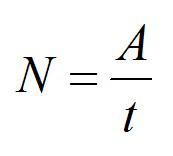
Мощность измеряется в Ваттах.
Нужна помощь в решении задач и других заданий? Обращайтесь в профессиональный студенческий сервис.
Автор
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Источник
У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.
Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.
Задачи по физике на КПД теплового двигателя
Задача на вычисление КПД теплового двигателя №1
Условие
Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.
Решение
Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:
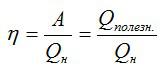
Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:
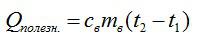
Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.
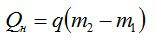
Подставляем значения и вычисляем:
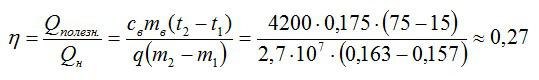
Ответ: 27%
Задача на вычисление КПД теплового двигателя №2
Условие
Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.
Решение
Найдем общее количество теплоты, которое произвел двигатель:
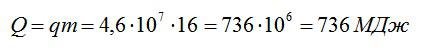
Теперь можно рассчитать КПД:
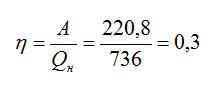
Или, умножая на 100, получаем значение КПД в процентах:
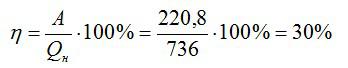
Ответ: 30%.
Задача на вычисление КПД теплового двигателя №3
Условие
Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.
Решение
КПД идеальной тепловой машины:
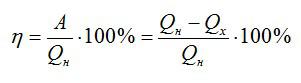
По условию:
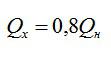
Вычислим сначала работу, а затем КПД:
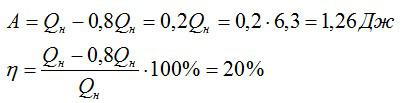
Ответ: 20%; 1,26 Дж.
Задача на вычисление КПД теплового двигателя №4
Условие
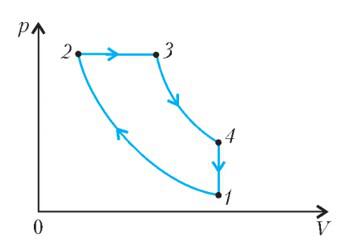
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.
Решение
Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.
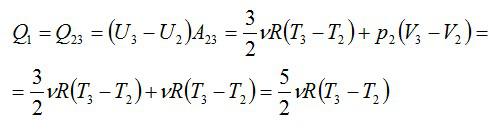
Аналогично:
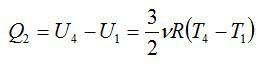
Получим результат:
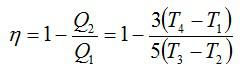
Ответ: См. выше.
Задача на вычисление КПД теплового двигателя №5
Условие
Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.
Решение
Запишем формулу для КПД:
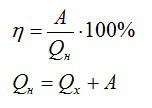
Отсюда:
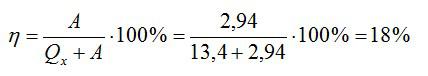
Ответ: 18%
Вопросы на тему тепловые двигатели
Вопрос 1. Что такое тепловой двигатель?
Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.
Вопрос 2. Приведите примеры тепловых двигателей.
Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:
- ракетный двигатель;
- авиационный двигатель;
- газовая турбина.
Вопрос 3. Может ли КПД двигателя быть равен единице?
Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.
КПД реальных двигателей редко превышает 30%.
Вопрос 4. Что такое КПД?
Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.
Вопрос 5. Что такое удельная теплота сгорания топлива?
Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.
Задачи и вопросы на цикл Карно
Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.
Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).
Задача на цикл Карно №1
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.
Решение
Рассчитаем КПД цикла:
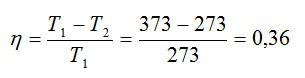
С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:
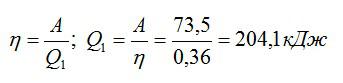
Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:
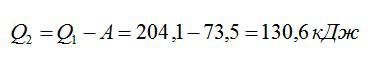
Ответ: 0,36; 204,1 кДж; 130,6 кДж.
Задача на цикл Карно №2
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.
Решение
Формула для КПД цикла Карно:
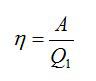
Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:
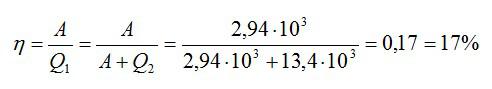
Ответ: 17%.
Задача на цикл Карно №3
Условие
Изобразите цикл Карно на диаграмме и опишите его
Решение
Цикл Карно на диаграмме PV выглядит следующим образом:

- 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
- 2-3. Адиабатическое расширение, тепло не подводится;
- 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
- 4-1. Адиабатическое сжатие.
Ответ: см. выше.
Вопрос на цикл Карно №1
Сформулируйте первую теорему Карно
Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.
Вопрос на цикл Карно №2
Может ли коэффициент полезного действия в цикле Карно быть равным 100%?
Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.
Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.
Источник

Еще один тип текстовых задач в вариантах ЕГЭ по математике — это задачи на работу.
Задачи на работу также решаются с помощью одной-единственной формулы: . Здесь — работа, — время, а величина , которая по смыслу является скоростью работы, носит специальное название — производительность. Она показывает, сколько работы сделано в единицу времени. Например, продавец в супермаркете надувает воздушные шарики. Количество шариков, которые он надует за час — это и есть его производительность.
Правила решения задач на работу очень просты.
- , то есть работа производительность время. Из этой формулы легко найти или .
- Если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу. Построен дом (один). Написана книга (одна). А вот если речь идет о количестве кирпичей, страниц или построенных домов — работа как раз и равна этому количеству.
- Если трудятся двое рабочих (два экскаватора, два завода…) — их производительности складываются. Очень логичное правило.
- В качестве переменной удобно взять именно производительность.
Покажем, как все это применяется на практике.
1. Заказ на деталей первый рабочий выполняет на час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на деталь больше?
Так же, как и в задачах на движение, заполним таблицу.
В колонке «работа» и для первого, и для второго рабочего запишем: . В задаче спрашивается, сколько деталей в час делает второй рабочий, то есть какова его производительность. Примем ее за . Тогда производительность первого рабочего равна (он делает на одну деталь в час больше). , время работы первого рабочего равно , время работы второго равно .
Первый рабочий выполнил заказ на час быстрее. Следовательно, на меньше, чем , то есть
Мы уже решали такие уравнения. Оно легко сводится к квадратному:
Дискриминант равен . Корни уравнения: , . Очевидно, производительность рабочего не может быть отрицательной — ведь он производит детали, а не уничтожает их 🙂 Значит, отрицательный корень не подходит.
Ответ: .
2. Двое рабочих, работая вместе, могут выполнить работу за дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?
В этой задаче (в отличие от предыдущей) ничего не сказано о том, какая это работа, чему равен ее объем. Значит, работу можем принять за единицу.
А что же обозначить за переменные? Мы уже говорили, что за переменную удобно обозначить производительность. Пусть — производительность первого рабочего. Но тогда производительность второго нам тоже понадобится, и ее мы обозначим за .
По условию, первый рабочий за два дня делает такую же часть работы, какую второй — за три дня. Значит, . Отсюда .
Работая вместе, эти двое сделали всю работу за дней. При совместной работе производительности складываются, значит,
.
Итак, первый рабочий за день выполняет всей работы. Значит, на всю работу ему понадобится дней.
Ответ: .
3. Первая труба пропускает на литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом литров она заполняет на минуты дольше, чем вторая труба заполняет резервуар объемом литров?
Всевозможные задачи про две трубы, которые наполняют какой-либо резервуар для воды — это тоже задачи на работу. В них также фигурируют известные вам величины — производительность, время и работа.
Примем производительность первой трубы за . Именно эту величину и требуется найти в задаче. Тогда производительность второй трубы равна , поскольку она пропускает на один литр в минуту больше, чем первая. Заполним таблицу
Первая труба заполняет резервуар на две минуты дольше, чем вторая. Значит, . Составим уравнение:
и решим его.
Ответ: .
. Андрей и Паша красят забор за часов. Паша и Володя красят этот же забор за часов, а Володя и Андрей — за часов. За сколько часов мальчики покрасят забор, работая втроем?
Мы уже решали задачи на движение. Правила те же. Отличие лишь в том, что здесь работают трое, и переменных будет тоже три. Пусть — производительность Андрея, — производительность Паши, а — производительность Володи. Забор, то есть величину работы, примем за — ведь мы ничего не можем сказать о его размере.
Андрей и Паша покрасили забор за часов. Мы помним, что при совместной работе производительности складываются. Запишем уравнение:
Аналогично,
Тогда
.
Можно искать , и по отдельности, но лучше просто сложить все три уравнения. Получим, что
Значит, работая втроем, Андрей, Паша и Володя красят за час одну восьмую часть забора. Весь забор они покрасят за часов.
Ответ: .
Читаем дальше: Задачи на проценты
Источник
