Выделение полезного сигнала на фоне помех
Библиографическое описание:
Орлов, П. В. Выделение сигнала на фоне коррелированных помех и некоррелированного шума / П. В. Орлов, В. Г. Андреев. — Текст : непосредственный // Молодой ученый. — 2019. — № 24 (262). — С. 145-148. — URL: https://moluch.ru/archive/262/60714/ (дата обращения: 25.10.2020).
В настоящее время широкое распространение получили бесплатформенные инерциальные навигационные системы (БИНС), которые реализуются на микромеханических гироскопах (измерителях угловой скорости) и акселерометрах (измерителях ускорений). Примером аппаратных средств, на которых реализована трёхосная (в трёх пространственных измерениях) БИНС, могут служить микромеханические изделия серии ADIS фирмы Analog Devices [1, 2].
Проблема начальной выставки БИНС дополнительно осложняется вибрациями корпуса носителя навигационной системы. Вибрации могут возникать из-за ветровых воздействий на носитель или вызываться работающими на нём механическими агрегатами. Так, например, если нет возможности провести начальную выставку при выключенных двигателях, то дисперсия сигналов на выходах акселерометров, как показали натурные эксперименты, может возрастать в тысячу и более раз по сравнению с ситуацией, когда двигатели не запущены.
Для подавления шумов акселерометров применяется низкочастотная фильтрация сигналов с их выходов, которая заключается в нахождении математического ожидания оценок, измеряемых по каждой оси ускорений. Подобный подход правомерен, если мешающие компоненты сигналов представляют собой некоррелированный шум [3]. Однако при вибрациях корпуса носителя БИНС предположение о некоррелированности мешающих компонент становится неверным [1].
Представим сигнал в виде:
x(t) = c(t) + s(t) + n(t),
где x(t) — наблюдаемый сигнал; c(t) — коррелированная помеха; s(t) — полезный сигнал; n(t) — некоррелированный шум.
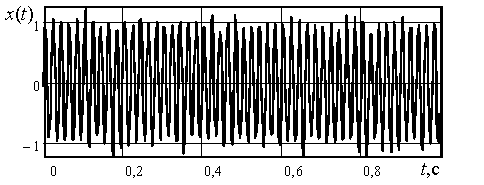
Рис.1. Наблюдаемый сигнал
Выделение полезной компоненты s(t) из смеси x(t) сводится к обелению коррелированной мешающей составляющей c(t) и накоплению полезного сигнала на фоне шума n(t). Известно [3], что коэффициенты импульсной характеристики обеляющего фильтра q‑го порядка могут быть найдены из выражения:
w=R−1i,
где w= [W0; W1; …; Wq] — вектор коэффициентов импульсной характеристики обеляющего фильтра (ОФ), R−1 — [(q+1)×(q+1)]‑мерная корреляционная матрица мешающего процесса, i= [1; 0;…; 0]T — крайний левый вектор-столбец единичной матрицы.
Структурная схема системы обработки сигнала x(t) представлена на рисунке 2. На нём использовано дискретное представление сигналов:
xn=x(t), yn=y(t), sn=s(t).
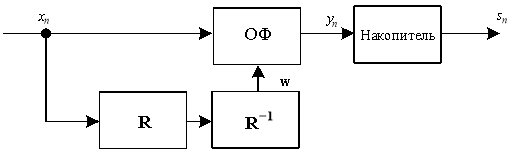
Рис.2. Система обработки акселерометрического сигнала
Выходной сигнал yn на выходе обеляющего фильтра сводится к виду:
yn=,
где yn — результат обеления; xn — входной сигнал; Wk — k‑й коэффициент импульсной характеристики w ОФ, k=0, 1, …, q.
Предлагаемый метод обработки выходных сигналов акселерометров подразумевает наличие коррелированной помехи c(t), вызванной дрожанием корпуса носителя БИНС. Помеха c(t) имеет регулярный колебательный характер, действующий по гармоническому закону. На рисунке 3 изображены нормированные к своим максимальным значениям квадраты амплитудно-частотные характеристики S(f) предлагаемого (сплошная жирная линия 3) и известного (пунктирная линия 1) фильтров обработки.
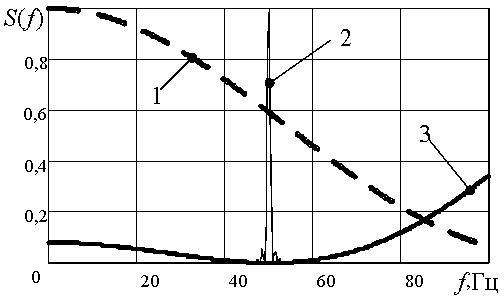
Рис. 3. Частотные характеристики
Под известным фильтром подразумевается равновесный нерекурсивный накопитель q‑го порядка. Кроме того, на рисунке 3 изображена тонкой сплошной линией 2 спектральная плотность мощности S(f) смеси коррелированной помехи c(t) и некоррелированного шума n(t). Порядки фильтров приняты q=3, измеренная доминантная частота fс коррелированной помехи fс=50 Гц.
На рисунках 4 и 5 изображены амплитудно-частотные характеристики S(f) для предлагаемого и известного методов при порядках фильтра q=20 и q=40 соответственно
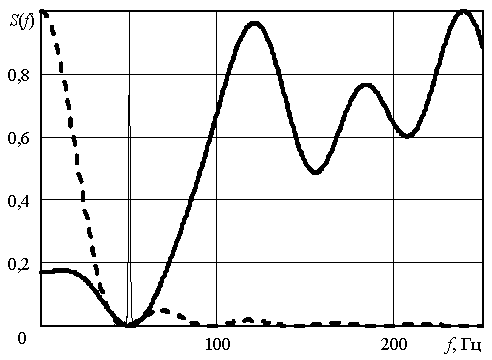
Рис. 4. Частотные характеристики при порядке фильтра q=20
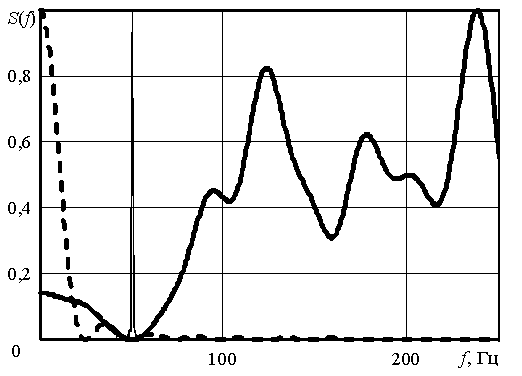
Рис. 5. Частотные характеристики при порядке фильтра q=40
Анализ приведенных на рисунках 3, 4 и 5 зависимостей показывает, что известный подход к обработке акселерометрических сигналов не предусматривает борьбу с коррелированной помехой, т. е. амплитудно-частотные характеристики не имеют провала на частоте воздействия помехи. Предлагаемое решение путём оценивания корреляционных свойств мешающего процесса адаптируется к его частоте и создаёт на ней глубокий провал амплитудно-частотной характеристики. Это даёт возможность подавить мешающую компоненту до уровня шумов, а затем путём накопления сигнала увеличить соотношение сигнал-шум на выходе системы обработки. Предлагаемое решение реализуется путём создания нерекурсивного обеляющего фильтра.
Литература:
- Андреев В. Г., Белокуров В. А. Метод повышения точности начальной выставки бесплатформенных навигационных систем // Вестник Рязанского государственного радиотехнического университета. № 2. Выпуск 36. 2011. С. 28‑33.
- Власенко А. Интегральные гироскопы iMEMS + датчики угловой скорости фирмы Analog Devices // Электронные компоненты. № 2. 2003. C. 36‑38.
- Воробьев С. Н. Цифровая обработка сигналов: Учебник для студентов учреждений высшего профессионального образования. М.: ИЦ Академия, 2013. 320 с.
Основные термины (генерируются автоматически): коррелированная помеха, импульсная характеристика, некоррелированный шум, обеляющий фильтр, порядок фильтра, ADIS, вибрация корпуса носителя, го порядка, начальная выставка, полезный сигнал.
Источник
§ 16. ФИЛЬТРЫ ДЛЯ СИГНАЛОВ ИЗВЕСТНОЙ ФОРМЫ
В гл. I и II мы считали, что сигнал и помеха являются случайными процессами с известными корреляционными свойствами. Как мы уже отмечали выше (см. § 7), в радиолокации, а также в ряде других областей радиотехники форма полезного сигнала, поступающего в приемник, является фиксированной. В этом случае полезный сигнал нужно рассматривать не как случайный процесс, а как заданную функцию с одним или несколькими неизвестными параметрами (амплитуда, время прихода, высокочастотная фаза и т. п.). Цель фильтрации заключается уже не в воспроизведении формы сигнала (известной) с минимумом средней квадратичной ошибки, а в наиболее надежном обнаружении полезного сигнала на фоне случайных помех и в наиболее точном изхмерении его параметров, в особенности времени прихода сигнала, фиксирующего расстояние до отражающего объекта. Поэтому качество фильтра, выделяющего сигналы известной формы, характеризуется отношением сигнал/помеха на выходе фильтра. Связь этого отношения с более тонкими вероятностными свойствами приемника будет исследована во второй части книги.
Предполагая, что полезный сигнал имеет вполне определенную форму, рассмотрим процесс его прохождения через линейный фильтр К с частотной характеристикой Л». На вход фильтра подается смесь полезного сигнала имеющего известную форму, и помехи представляющей собой стационарный случайный процесс,
Полезный сигнал может отсутствовать, тогда на выходе фильтра имеется одна помеха
Мы будем сначала считать, что функция полностью известна, так что искомый фильтр должен максимально облегчить обнаружение полезного сигнала, т. е. помочь решить, какая из возможностей – (16.01) или – реализуется в данном опыте. Более сложный случа, когда сигнал зависит от неизвестных параметров, будет рассмотрен в конце параграфа. На выходе фильтра при наличии сигнала мы получаем функцию
где есть результат преобразования полезного сигнала фильтром результат преобразования помехи. Сигнал можно, например, себе представить в виде прямоугольных радиоимпульсов, часто применяемых в радиолокации. Считая, что полезный сигнал имеет конечную длительность (или достаточно быстро стремится к нулю при мы можем разложить его в интеграл Фурье
где
Функция полезный сигнал на выходе фильтра К — равна
где формулу (2.23)] есть комплексная частотная характеристика фильтра К.
Для случайного процесса — помехи — вместо спектральных выражений вида (16.06) следует воспользоваться теоремой Хинчина (см. § 3), согласно которой, в частности, можно написать
Здесь есть интенсивность помехи (черта означает образование статистического среднего), спектральная интенсивность помехи на входе фильтра. На выходе фильтра К помеха будет иметь согласно формуле (3.09) интенсивность
Отношение сигнал/помеха (по мощности) на выходе фильтра мы будем определять выражением
где значение сигнала на выходе в некоторый момент Пользуясь формулами (16.06) и (16.08), получим
Будем искать фильтр, который бы давал на выходе наибольшее значение по сравнению со всеми остальными. Это значит, что мы будем принимать решение по значению
поэтому нам важно, чтобы слагаемое по своей абсолютной величине как можно более превосходило
Частотную характеристику искомого фильтра можно найти из следующего неравенства
которое показывает, что
Мы получили таким образом верхний предел для Если взять
где с — произвольная константа, то такой фильтр будет давать максимально достижимое значение равное
Неравенство (16.12) является обобщением известного алгебраического неравенства Шварца-Буняковского. Чтобы его доказать, возьмем двойной интеграл
поскольку исходный интеграл отрицательных значений принимать не может. Учитывая, что
мы получим неравенство
для любых двух функций и если выписанные интегралы имеют смысл (сходятся). Полагая
мы и приходим к неравенству (16.12).
Таким образом, среди линейных фильтров наилучшим является фильтр с частотной характеристикой (16.14). Если помеха есть нормальный случайный процесс, то такой фильтр является абсолютно оптимальным, как мы покажем во второй части книги. Поэтому нелинейные фильтры могут иметь значение лишь при помехах, не являющихся нормальными, а тогда математическое исследование оптимальных фильтров и оптимальных приемников усложняется настолько, что ощутимых практических результатов получить не удается.
Физический смысл формулы (16.14) очень прост: оптимальный линейный фильтр К пропускает элементарный интервал частот в тем большей степени, чем больше спектральная амплитуда полезного сигнала и чем меньше спектральная интенсивность помех в этом интервале. Формула (16.15) при этом показывает, что отношение сигнал/помеха на выходе такого фильтра тем больше, чем больше отличие спектра сигнала от спектра помехи (ср. конец § 2). Так, например, если спектральная интенсивность весьма мала в некоторой части частотного диапазона, занятого сигналом, то оптимальный фильтр К будет пропускать практически только эту часть диапазона, и величина (16.15) будет весьма большой. Полезный сигнал на выходе фильтра сильно отличается по форме от сигнала на его входе (ср. далее § 17 и 20), однако эта форма известна и поэтому никаких опасностей при ее искажении не возникает.
Заметим, что из формул (16.06) и (16.14) вытекает соотношение
откуда (ср. § 3)
При использовании данного фильтра для обнаружения полностью известного сигнала нужно только значение (16.11), т. е. значение выходной функции фильтра в один определенный момент времени, поскольку в другие моменты согласно формуле (16.21) полезный сигнал на выходе фильтра меньше. Если же полезный сигнал имеет вид
т. е. зависит от неизвестных параметров амплитуда, время появления сигнала, известная функция времени), то результаты несколько изменяются. Прежде всего, по формуле (16.05) мы будем иметь
где
так что функция зависит от неизвестных параметров. Чтобы не вводить в формулу (16.14) неизвестного параметра ее приходится изменить следующим образом:
так как в противном случае мы должны применять столько фильтров, сколько имеется возможных значений Формула (16.20) тогда принимает вид:
так что
где
есть отношение сигнал/помеха на выходе фильтра с частотной характеристикой (16.25), определяемое с помощью соотношения
При произвольном отношение сигнал/помеха можно определить по формуле
или же пользоваться усредненным параметром
где вычисляется в соответствии с законом распределения случайной величины
Очевидно, что частотная характеристика (16.25) обеспе чивает максимальное значение параметров (16.30) и (16.31), причем в данном случае процесс на выходе фильтра используется более полно: а именно, если параметр может принимать значения то необходимы значения . В частности, если может принимать все значения в интервале 0 то нужно использовать функцию при Если помехи отсутствуют то получающаяся таким образом функция позволит полностью определить параметры находится по положению максимума функции по величине этого максимума [см. формулу (16.27)]. Слабые помехи большие значения приводят, очевидно, к некоторым ошибкам в определении поскольку помехи случайным образом смещают максимум [по отношению к максимуму так, что положение максимума на оси и его абсолютная величина изменяются. При увеличении помех (т. е. при уменьшении эти ошибки растут, причем при достаточно больших помехах (достаточно малых наличие или отсутствие полезного сигнала почти полностью маскируется помехами и даже оптимальный фильтр, обеспечивающий максимальное значение не может выделить сигнала на фоне помех. Такова качественная картина работы оптимального линейного фильтра.
Заметим в заключение, что если в формуле (16.14) положить , то в силу соотношений (16.09) и (16.21) мы будем иметь
Таким образом, параметр —отношение сигнал/помеха — дает нам одновременно полезный сигнал и интенсивность помех на выходе оптимального линейного фильтра. Отметим также интересное соотношение
связывающее полезный сигнал и корреляционную функцию помех на выходе оптимального фильтра. Аналогичные формулы можно вывести для частотной характеристики (16.25).
Источник
— операция подавления мешающих действий помех и повышения качества передачи полезного (несущего информацию) сигнала в результате восстановления мгновенных значений этого сигнала с заданной вероятностью ошибки. При этом эффективность выделения полезного сигнала можно оценивать функцией вероятности того, что отклонение выделенного сигнала от его истинного значения не превышает некоторого заранее заданного порога
В общем случае В. с. на ф. п. основываются на априорных сведениях о параметрах (отличительных признаках) сигнала и помех. Различие спектральных характеристик, интенсивностей, временных свойств, фазовых соотношений сигнала и помех позволяет осуществить функциональную (частотную, амплитудную, временную, фазовую и др.) избирательность в системе выделения сигнала и ослабить в определенной мере метающие влияния помех. Наибольшее распространение получила частотная избирательность.
Сов. ученый-радиотехник В. А. Котельников (р. 1908) и амер. ученый Ф. Вудворд независимо один от другого обосновали принципиальную возможность оптимального выделения (приема) сигналов, обеспечивающую макс. вероятность правильного воспроизведения полезного сигнала. Выделение сигнала в этом случае рассматривается как задача определения на основе анализа реализации принятого сигнала условной вероятности того, что принятому сигналу у соответствует определенный полезный сигнал . Полезный сигнал при этом рассматривается, как случайный объект с известным законом распределения в соответствующем пространстве. Определение условной вероятности позволяет наилучшим образом уменьшить априорную неопределенность в отношении принимаемого сигнала. При известном законе распределения вероятностей полезного сигнала нахождение можно свести к определению условной вероятности того, что известному сигналу соответствует принятый сигнал у, так как , где k — постоянная; обычно наз. ф-цией правдоподобия и обозначают Решение о выделении (приеме) определенного сигнала принимается по максимуму ф-ции правдоподобия.
Оптим. выделение (прием) полезного сигнала можно осуществить и без определения условных вероятностей или достаточно, чтобы результат обработки смеси полезного сигнала и помехи однозначно определялся этими распределениями. Так, для оптим. выделения сигпала действующего на фоне белого шума с нормальным законом распределения амплитуд в течение времени Т, достаточно определить корреляционный интеграл
где смесь полезного сигнала и помех. Такая операция позволяет извлечь наибольшее количество информации о наличии сигнала, поскольку по значениям однозначно определяется ф-ция правдоподобия Это доказывает оптимальность приемника взаимно-корреляционного типа.
Устройство выделения сигнала можно рассматривать как линейный фильтр, обрабатывающий смесь так, что выходной сигнал наилучшим (в рамках принятого критерия) образом воспроизводит полезный сигнал Такое устройство наз. оптим. фильтром, а сам процесс выделения — оптим. фильтрацией. Основы теории оптим. фильтрации заложены в работах сов. математика А. Н. Колмогорова (р. 1903) и амер. математика Н. Винера (1894—1964).
Взаимно-корреляционный приемник можно рассматривать как оптимальный по критерию максимума информации фильтр, а его выходной сигнал в момент — как реакцию фильтра с импульсной характеристикой, тождественно равной зеркальному изображению сигнала
Частотная характеристика такого фильтра с точностью до постоянного множителя совпадает с комплексно сопряженным спектром полезного сигнала :
Будучи оптимальным в информационном смысле, взаимно-корреляционный приемник максимизирует отношение пикового значения сигнала к эффективному значению помехи. Это отношение равно отношению полной энергии сигнала к спектральной плотности мощности Е шума не зависит от формы полезного сигнала. Фильтры выделения полезного сигнала можно оптимизировать по критерию минимума среднеквадратичного уклонения
Частотная характеристика такого оптимального фильтра для статистически независимых сигнала и помех однозначно определяется формой энергетического спектра полезного сигнала и помех
В практике для В. с. на ф. п. широко применяют квазиоптимальные фильтры, форма частотной характеристики которых в известной степени произвольна и не зависит от спектров сигнала и помех, а полоса пропускания согласована с ними. Отношение сигнала к помехе на выходе таких фильтров хуже, чем у оптимальных.
Лит.: Колмогоров А. Н. Интерполирование и экстраполирование стационарных случайных последовательностей. «Известия АН СССР. Серия математическая», 1941, т. 5, № 1; Котельников В. А. Теория потенциальной помехоустойчивости. М. – Л., 1956; Гуткин Л. С. Теория оптимальных методов радиоприема при флуктуационных помехах. М. – Л., 1961 [библиогр. с. 479-484]; Wiener N. Extrapolation, interpolation and smoothing of stationary time series. New York, 1950: W oodward P. M. Probability and information theory, with applications to radar. London, 1955. B. И. Чайковский.
Источник
По роду своей деятельности мне приходится осуществлять контроль различных параметров наземных импульсно-фазовых радионавигационных систем (ИФРНС) «Чайка» и Loran-C. В этой статье я хочу поделиться одним из методов обнаружения времени прихода импульса ИФРНС при наличии шумов. Метод применим во многих задачах поиска сигнала известной формы.
Системы относятся к классу гиперболических систем и основаны на измерении разности времени прихода радиоимпульсов, принимаемых от цепочки передающих станций. В каждой цепочке одна из станций является ведущей, а остальные – ведомые. Все они точно синхронизируются.
Основной проблемой при детектировании сигналов ИФРНС является искажение формы принимаемых радиоимпульсов за счет наложения на поверхностную волну отраженных составляющих. Составляющие сигнала, которые не распространяются вдоль поверхности, проходят различные пути за различное время. Невозможно надежно предсказать время их прихода. Однако, очевидно, что отраженные составляющие сигнала распространяются медленнее поверхностной составляющей. Они также влияют на форму принимаемого сигнала. Форма принимаемого радиоимпульса может изменяться в зависимости от времени года, времени суток, а также от погодных условий и географической местности. Для выполнения задач навигации необходим алгоритм выделения начала поверхностной составляющей радиоимпульса.
Принимаемый сигнал xt (t) во временной области может быть представлен следующим уравнением:
(1)
где xg (t) – поверхностная составляющая, амплитуда и задержка n-ной отраженной составляющей определяются коэффициентами kn и tn, а e (t) — шумовая компонента.
Ниже изображены эталонный импульс ИФРНС и его спектр после прохождения полосового фильтра приемника. Частота дискретизации составляет 5 МГц.
В качестве примера рассмотрим смоделированный радиоимпульс, состоящий из поверхностной и отраженной составляющих. На рисунках ниже представлены графики, на котором изображена модель импульса, состоящая из двух составляющих смещенных друг от друга на 130 мкс. Амплитуда отраженной составляющей в 2 раза ниже амплитуды поверхностной составляющей.
Эквивалентное представление сигнала в частотной области описывается как:
(2)
где Xt (f), Xg (F) и E (f) — спектры сигналов xt (t), xg (t) и e (t).
Примем, что спектр эталонного нормированного сигнала системы «Лоран-С» или «Чайка» обозначается как X0 (f).
Очевидно, что
(3)
где kg — амплитуда поверхностной составляющей. Если выражение для Xg (f) из формулы (3) подставить в формулу (2) и разделить почленно все слагаемые на X0 (f), получится выражение
(4)
На рисунке ниже изображен график результата деления спектра сигнала на спектр эталона. Изображенный красным, график представляет собой горизонтальную пилообразную линию во всей области частот.
Обратное преобразование Фурье над выражением (4) дает формулу
(5)
Математический смысл выражения (5) заключается в том, что во временной области мы получаем пики в виде дельта-функций в моменты появления как поверхностной, так и всех отраженных составляющих сигнала, нормированные по амплитуде.
На рисунке ниже изображен график детектирования начала составляющих сигнала. Как видно из графика отношение амплитуд составляющих сигнала равно двум и расстояние между пиками составляет 130 мкс, что соответствует параметрам построенной модели.
Метод обычного деления спектров хорошо действует для идеальных сигналов. При добавлении в сигнал шумовой составляющей эффективность метода резко ухудшается. На рисунках ниже изображен график детектирования начала сигнала при соотношении сигнал/шум 25 дБ. Как видно из рисунков определение начала сигналов выполнить невозможно.
На графике спектра можно заметить, что внутри полосы шириной приблизительно 30 кГц с центром в точке 100 кГц результат деления спектров имеет горизонтальный пилообразный вид как при использовании метода деления спектров на идеальном не зашумленном сигнале. Использование прямоугольного окна шириной 30 кГц с центром в точке 100 кГц позволяет устранить влияние шумов перед операцией обратного преобразования Фурье. На рисунке ниже изображен график детектирования начала сигнала при использовании оконной фильтрации зашумленного сигнала. Два максимума графика позволяют обнаружить начало каждой из составляющих сигнала на фоне шума и также оценить отношение их амплитуд.
Метод деления спектров с применением оконного сглаживания эффективен при соотношении сигнал/шум выше 12 дБ. Наиболее эффективным типом окна признано прямоугольное окно с полосой 30 кГц. На рисунках ниже изображен реальный импульс цепочки Northern Sea of China Chain и график обнаружения его начала.
Оригинальная статья расположена здесь. Алгоритм в настоящее время применяется мной для контроля параметров станций ИФРНС Дальневосточного региона.
Источник
