Во сколько раз увеличиться коэффициент полезного действия цикла карно

6.3. Второй закон термодинамики
6.3.1. Коэффициент полезного действия тепловых двигателей. Цикл Карно
Второе начало термодинамики возникло из анализа работы тепловых двигателей (машин). В формулировке Кельвина оно выглядит следующим образом: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.
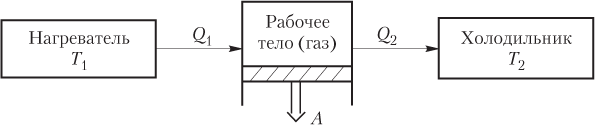
Схема действия тепловой машины (теплового двигателя) представлена на рис. 6.3.
Рис. 6.3
Цикл работы теплового двигателя состоит из трех этапов:
1) нагреватель передает газу количество теплоты Q
1;
2) газ, расширяясь, совершает работу A;
3) для возвращения газа в исходное состояние холодильнику передается теплота Q
2.
Из первого закона термодинамики для циклического процесса
Q = A,
где Q — количество теплоты, полученное газом за цикл, Q = Q
1 − Q
2; Q
1 — количество теплоты, переданное газу от нагревателя; Q
2 — количество теплоты, отданное газом холодильнику.
Поэтому для идеальной тепловой машины справедливо равенство
Q
1 − Q
2 = A.
Когда потери энергии (за счет трения и рассеяния ее в окружающую среду) отсутствуют, при работе тепловых машин выполняется закон сохранения энергии
Q
1 = A + Q
2,
где Q
1 — теплота, переданная от нагревателя рабочему телу (газу); A — работа, совершенная газом; Q
2 — теплота, переданная газом холодильнику.
Коэффициент полезного действия тепловой машины вычисляется по одной из формул:
η=AQ1⋅100 %, η=Q1−Q2Q1⋅100 %, η=(1−Q2Q1)⋅100 %,
где A — работа, совершенная газом; Q
1 — теплота, переданная от нагревателя рабочему телу (газу); Q
2 — теплота, переданная газом холодильнику.
Наиболее часто в тепловых машинах используется цикл Карно, так как он является самым экономичным.
Цикл Карно состоит из двух изотерм и двух адиабат, показанных на рис. 6.4.
Рис. 6.4
Участок 1–2 соответствует контакту рабочего вещества (газа) с нагревателем. При этом нагреватель передает газу теплоту Q
1 и происходит изотермическое расширение газа при температуре нагревателя T
1. Газ совершает положительную работу (A
12 > 0), его внутренняя энергия не изменяется (∆U
12 = 0).
Участок 2–3 соответствует адиабатному расширению газа. При этом теплообмена с внешней средой не происходит, совершаемая положительная работа A
23
приводит к уменьшению внутренней энергии газа: ∆U
23
= −A
23
, газ охлаждается до температуры холодильника T
2.
Участок 3–4 соответствует контакту рабочего вещества (газа) с холодильником. При этом холодильнику от газа поступает теплота Q
2 и происходит изотермическое сжатие газа при температуре холодильника T
2. Газ совершает отрицательную работу (A
34 < 0), его внутренняя энергия не изменяется (∆U
34 = 0).
Участок 4–1 соответствует адиабатному сжатию газа. При этом теплообмена с внешней средой не происходит, совершаемая отрицательная работа A
41
приводит к увеличению внутренней энергии газа: ∆U
41
= −A
41
, газ нагревается до температуры нагревателя T
1, т.е. возвращается в исходное состояние.
Коэффициент полезного действия тепловой машины, работающей по циклу Карно, вычисляется по одной из формул:
η=T1−T2T1⋅100 %, η=(1−T2T1)⋅100 %,
где T
1 — температура нагревателя; T
2 — температура холодильника.
Пример 9. Идеальная тепловая машина совершает за цикл работу 400 Дж. Какое количество теплоты передается при этом холодильнику, если коэффициент полезного действия машины равен 40 %?
Решение. Коэффициент полезного действия тепловой машины определяется формулой
η=AQ1⋅100 %,
где A — работа, совершаемая газом за цикл; Q
1 — количество теплоты, которое передается от нагревателя рабочему телу (газу).
Искомой величиной является количество теплоты Q
2, переданное от рабочего тела (газа) холодильнику, не входящее в записанную формулу.
Связь между работой A, теплотой Q
1, переданной от нагревателя газу, и искомой величиной Q
2 устанавливается с помощью закона сохранения энергии для идеальной тепловой машины
Q
1 = A + Q
2.
Уравнения образуют систему
η=AQ1⋅100 %,Q1=A+Q2,}
которую необходимо решить относительно Q
2.
Для этого исключим из системы Q
1, выразив из каждого уравнения
Q1=Aη⋅100 %,Q1=A+Q2}
и записав равенство правых частей полученных выражений:
Aη⋅100 %=A+Q2.
Искомая величина определяется равенством
Q2=Aη⋅100 %−A=A(100 %η−1).
Расчет дает значение:
Q2=400⋅(100 %40 %−1)=600 Дж.
Количество теплоты, переданной за цикл от газа холодильнику идеальной тепловой машины, составляет 600 Дж.
Пример 10. В идеальной тепловой машине от нагревателя к газу поступает 122 кДж/мин, а от газа холодильнику передается 30,5 кДж/мин. Вычислить коэффициент полезного действия данной идеальной тепловой машины.
Решение. Для расчета коэффициента полезного действия воспользуемся формулой
η=(1−Q2Q1)⋅100 %,
где Q
2 — количество теплоты, которое передается за цикл от газа холодильнику; Q
1 — количество теплоты, которое передается за цикл от нагревателя рабочему телу (газу).
Преобразуем формулу, выполнив деление числителя и знаменателя дроби на время t:
η=(1−Q2/tQ1/t)⋅100 %,
где Q
2/t — скорость передачи теплоты от газа холодильнику (количество теплоты, которое передается газом холодильнику в секунду); Q
1/t — скорость передачи теплоты от нагревателя рабочему телу (количество теплоты, которое передается от нагревателя газу в секунду).
В условии задачи скорость передачи теплоты задана в джоулях в минуту; переведем ее в джоули в секунду:
- от нагревателя газу —
Q1t=122 кДж/мин=122⋅10360 Дж/с;
- от газа холодильнику —
Q2t=30,5 кДж/мин=30,5⋅10360 Дж/с.
Рассчитаем коэффициент полезного действия данной идеальной тепловой машины:
η=(1−30,5⋅10360⋅60122⋅103)⋅100 %=75 %.
Пример 11. Коэффициент полезного действия тепловой машины, работающей по циклу Карно, равен 25 %. Во сколько раз увеличится коэффициент полезного действия, если температуру нагревателя увеличить, а температуру холодильника уменьшить на 20 %?
Решение. Коэффициент полезного действия идеальной тепловой машины, работающей по циклу Карно, определяется следующими формулами:
- до изменения температур нагревателя и холодильника —
η1=(1−T2T1)⋅100 %,
где T
1 — первоначальная температура нагревателя; T
2 — первоначальная температура холодильника;
- после изменения температур нагревателя и холодильника —
η2=(1−T′2T′1)⋅100 %,
где T′1 — новая температура нагревателя, T′1=1,2T1; T′2 — новая температура холодильника, T′2=0,8T2.
Уравнения для коэффициентов полезного действия образуют систему
η1=(1−T2T1)⋅100 %,η2=(1−0,8T21,2T1)⋅100 %,}
которую необходимо решить относительно η2.
Из первого уравнения системы с учетом значения η1 = 25 % найдем отношение температур
T2T1=1−η1100 %=1−25 %100 %=0,75
и подставим во второе уравнение
η2=(1−0,81,2⋅0,75)⋅100 %=50 %.
Искомое отношение коэффициентов полезного действия равно:
η2η1=50 %25 %=2,0.
Следовательно, указанное изменение температур нагревателя и холодильника тепловой машины приведет к увеличению коэффициента полезного действия в 2 раза.
Источник
В термодинамике цикл Карно́ или процесс Карно — это идеальный[1]круговой процесс, состоящий из двух адиабатных и двух изотермических процессов[2]. В процессе Карно термодинамическая система выполняет механическую работу за счёт обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником[3].
Цикл Карно назван в честь французского учёного и инженера Сади Карно, который впервые его описал в своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу» в 1824 году[4][5].
Поскольку идеальные процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному процессу Карно только с большей или меньшей степенью точности.
Коэффициент полезного действия (КПД) любой тепловой машины не может превосходить КПД идеальной тепловой машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника[6]. По этой причине, позволяя оценить верхний предел КПД тепловой машины, цикл Карно важен для теории тепловых машин. В то же время КПД цикла Карно настолько чувствителен к отклонениям от идеальности (потерям на трение), что данный цикл никогда не применяли в реальных тепловых машинах[K 1][8].
Описание цикла Карно[править | править код]
Рис. 1. Цикл Карно в координатах T—S
Рис. 2. Цикл Карно в координатах p—V
Рис. 3. Цикл Карно на термодинамической поверхности идеального газа
Пусть тепловая машина состоит из нагревателя с температурой , холодильника с температурой и рабочего тела.
Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах (температура) и (энтропия).
1. Изотермическое расширение (на рис. 1 — процесс A→B). В начале процесса рабочее тело имеет температуру , то есть температуру нагревателя. При расширении рабочего тела его температура не падает за счет передачи от нагревателя количества теплоты , то есть расширение происходит изотермически (при постоянной температуре) . При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.
2. Адиабатическое расширение (на рис. 1 — процесс B→C). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника , тело совершает механическую работу, а энтропия остаётся постоянной.
3. Изотермическое сжатие (на рис. 1 — процесс C→D). Рабочее тело, имеющее температуру , приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты . Над телом совершается работа, его энтропия уменьшается.
4. Адиабатическое сжатие (на рис. 1 — процесс D→A). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.
Обратный цикл Карно[править | править код]
В термодинамике холодильных установок и тепловых насосов рассматривают обратный цикл Карно, состоящий из следующих стадий[9][10]: адиабатического сжатия за счёт совершения работы (на рис. 1 — процесс В→Б); изотермического сжатия с передачей теплоты более нагретому тепловому резервуару (на рис. 1 — процесс Б→А); адиабатического расширения (на рис. 1 — процесс А→Г); изотермического расширения с отводом теплоты от более холодного теплового резервуара (на рис. 1 — процесс Г→В).
КПД тепловой машины Карно[править | править код]
Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно
Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику
Отсюда коэффициент полезного действия тепловой машины Карно равен
Первая и вторая теоремы Карно[править | править код]
Из последнего выражения следует, что КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела. Этот результат составляет содержание первой теоремы Карно[11]. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.
Поэтому максимальный КПД любой тепловой машины не может превосходить КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Это утверждение называется второй теоремой Карно[12][13]. Оно даёт верхний предел КПД любой тепловой машины и позволяет оценить отклонение реального КПД от максимального, то есть потери энергии вследствие неидеальности тепловых процессов.
Связь между обратимостью цикла и КПД[править | править код]
Для того чтобы цикл был обратимым, в нём должна быть исключена передача теплоты при наличии разности температур, иначе нарушается условие адиабатичности процесса. Поэтому передача теплоты должна осуществляться либо в изотермическом процессе (как в цикле Карно), либо в эквидистантном процессе (обобщённый цикл Карно или, для примера, его частный случай Цикл Брайтона). Для того чтобы менять температуру рабочего тела от температуры нагревателя до температуры холодильника и обратно, необходимо использовать либо адиабатические процессы (они идут без теплообмена и, значит, не влияют на энтропию), либо циклы с регенерацией тепла при которых нет передачи тепла при разности температур. Мы приходим к выводу, что любой обратимый цикл может быть сведён к циклу Карно.
Примером обратимого цикла, не являющегося циклом Карно, но интегрально совпадающим с ним, является идеальный цикл Стирлинга: в двигателе Стирлинга добавлен регенератор, обеспечивающий полное приближение цикла к циклу Карно с достижением обратимости и тех же величин КПД[14]. Возможны и другие идеальные циклы, в которых коэффициент полезного действия определяется по той же формуле, что и для циклов Карно и Стирлинга, например цикл Эрикссона (англ.)русск., состоящий из двух изобар и двух изотерм[14].
Если же в цикле возникает передача теплоты при наличии разности температур, а таковыми являются все технические реализации термодинамических циклов, то цикл утрачивает свойство обратимости. Иначе говоря, посредством отведённой в цикле механической работы становится невозможным получить исходную теплоту. КПД такого цикла будет всегда меньше, чем КПД цикла Карно.
См. также[править | править код]
- Термодинамические циклы
- Первое начало термодинамики
- Второе начало термодинамики
- Термодинамическая энтропия
- Термодинамические потенциалы
Комментарии[править | править код]
- ↑ В реальных тепловых машинах цикл Карно не используют, поскольку практически невозможно осуществить процессы изотермического сжатия и расширения. Кроме того, полезная работа цикла, представляющая собой алгебраическую сумму работ во всех четырех составляющих цикл частных процессах, даже в идеальном случае полного отсутствия потерь мала по сравнению с работой в каждом из частных процессов, то есть мы имеем дело с обычной ситуацией, когда итоговый результат представляет собой малую разность больших величин. Применительно к математическим вычислениям это означает высокую отзывчивость результата даже на небольшие вариации значений исходных величин, а в рассматриваемом нами случае соответствует высокой чувствительности полезной работы цикла Карно и его КПД к отклонениям от идеальности (потерям на трение). Эта связь с отклонениями от идеальности настолько велика, что с учетом всех потерь полезная работа цикла Карно приближается к нулю[7].
Примечания[править | править код]
- ↑ То есть без потерь, в первую очередь на трение.
- ↑ Карно цикл // Италия — Кваркуш. — М. : Советская энциклопедия, 1973. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 11).
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 94.
- ↑ Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. — Paris: Gauthier-Villars, Imprimeur-Libraire, 1878. — 102 p. (фр.)
- ↑ Второе начало термодинамики. (Работы Сади Карно — В. Томсон — Кельвин — Р. Клаузиус — Л. Больцман — М. Смолуховский) / Под. ред. А. К. Тимирязева. — Москва—Ленинград: Государственное технико-теоретическое издательство, 1934. — С. 17—61.
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 113—114.
- ↑ Бэр Г. Д., Техническая термодинамика, 1977, с. 112.
- ↑ Кинан Дж., Термодинамика, 1963, с. 93.
- ↑ Николаев Г. П., Лойко А. Э., Техническая термодинамика, 2013, с. 172.
- ↑ Бахшиева Л. Т. и др., Техническая термодинамика и теплотехника, 2008, с. 148.
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 95.
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 113.
- ↑ Румер Ю. Б., Рывкин М. Ш., Термодинамика, статистическая физика и кинетика, 2000, с. 35.
- ↑ 1 2 Крестовников А. Н., Вигдорович В. Н., Химическая термодинамика, 1973, с. 63.
Литература[править | править код]
- Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. — Paris: Gauthier-Villars, Imprimeur-Libraire, 1878. — 102 p. (фр.)
- Бахшиева Л. Т., Кондауров Б. П., Захарова А. А., Салтыкова В. С. Техническая термодинамика и теплотехника / Под ред. проф А. А. Захаровой. — 2-е изд., испр. — М.: Академия, 2008. — 272 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-4999-1.
- Бэр Г. Д. Техническая термодинамика. — М.: Мир, 1977. — 519 с. (недоступная ссылка)
- Кинан Дж. Термодинамика / Пер с англ. А. Ф. Котина под ред. М. П. Вукаловича. — М.—Л.: Госэнергоиздат, 1963. — 280 с.
- Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 3-е, доп. — М.: Наука, 1976. — 584 с. — («Теоретическая физика», том V).
- Крестовников А. Н., Вигдорович В. Н. Химическая термодинамика. — 2-е изд., испр. и доп. — М.: Металлургия, 1973. — 256 с.
- Николаев Г. П., Лойко А. Э. Техническая термодинамика. — Екатеринбург: УрФУ, 2013. — 227 с.
- Румер Ю. Б., Рывкин М. Ш. Термодинамика, статистическая физика и кинетика. — 2-е изд., испр. и доп. — Новосибирск: Изд-во Носиб. ун-та, 2000. — 608 с. — ISBN 5-7615-0383-2.
- Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.
- Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика. — 5 изд., испр.. — М.: ФИЗМАТЛИТ, 2005. — 544 с. — ISBN 5-9221-0601-5.
Источник
Циклический процесс– совокупнось термодинамических процессов, в результате которых система возвращается в исходное состояние. На диаграммах состояния р – V (рис. 67) круговые процессы изображаются замкнутыми кривыми.
Работа, совершаемая газом за цикл, определяется площадью, охватываемой кривой; изменение внутренней энергии равно нулю:
.(3.2.32)
Первое начало термодинамикидля круговых процессов имеет вид
,(3.2.33)
где знак означает интегрирование по замкнутому контуру.
Прямым цикломназывается круговой процесс, в котором система совершает положительную работу
.(3.2.34)
Замкнутая кривая на диаграмме, изображающая прямой цикл, описывается по часовой стрелке.
Обратным циклом называется круговой процесс, в котором система совершает отрицательную работу
.(3.2.35)
На диаграмме обратный цикл изображается замкнутой кривой, проходимой против часовой стрелки.
Обратимый процесс– это такой термодинамический процесс, при котором изменение состояния системы, будучи проведено в обратном направлении, возвращает ее в исходное состояние так, чтобы система прошла через те же промежуточные состояния, что и в прямом процессе, но в обратной последовательности, а состояние тел вне системы осталось бы неизменным.
Необратимый процесс– это такой термодинамический процесс, после окончания которого систему нельзя вернуть в начальное состояние так, чтобы нигде в среде не осталось никаких изменений.
Любая тепловая машина состоит из трех частей – нагревателя, холодильника и рабочего тела.
Рабочее тело– термодинамическая система, совершающая круговой процесс и обменивающаяся энергией с другими телами. Обычно рабочим телом является газ.
Нагреватель(теплоотдатчик) – тело, сообщающее термодинамическойсистеме энергию в форме некоторого количества теплоты.
Холодильник(теплоприемник) – тело, получающее от термодинамическойсистемы энергию в виде некоторого количества теплоты.
Термодинамическийкоэффициент полезного действия тепловой машины – отношение полезной работы (работы, совершенной рабочим телом в рассматриваемом прямом круговом процессе) к сумме всех количеств тепла, сообщенных рабочему телу нагревателями:
,(3.2.36)
где – количество теплоты, полученное рабочим телом от нагревателя при температуре Т1,
– количество теплоты, Отданное рабочим телом холодильнику при температуре Т2,
А – работа, совершенная тепловой машиной за цикл,
h – термодинамический коэффициент полезного действия тепловой машины.
КПД цикла Карно
Цикл Карно– прямой круговой процесс, при котором выполненная системой работа максимальна. Цикл состоит из двух изотермических и двух адиабатических расширений и сжатий (рис. 68)
В процессе 1 – 1′ рабочее тело получает от нагревателя количество теплоты , а в процессе 2 – 2′ – рабочее тело отдает холодильнику количество, теплоты
Теорема Карно. Тепловая машина при данных значениях температур нагревателя и холо дильника, не может иметь большего КПД, чем машина, работающая по обратимому циклу Карно при тех же значениях температур нагревателя и холодильника.
Термический коэффициент полезного действия обратимого цикла Карно не зависит от природы рабочего тела и является функцией только абсолютных температур нагревателя – Т1 и холодильника Т2.
.(3.2.37)
Вобратимом цикле Карно выполняется соотношение:
,(3.2.38)
где Т1 – температура нагревателя, Т2 –температура холодильника, – количество теплоты, переданное системе нагревателем, – количество теплоты, переданное системой холодильнику.
Термический КПД произвольного обратимого цикла:
,(3.2.39)
где Тmах и Тmin – экстремальные значения температуры нагревателя и холодильника, участвующих в осуществлении рассматриваемого цикла.
Второе начало термодинамики
Первое начало термодинамики, выражает закон сохранения и превращения энергии для тепловых процессов, но не позволяет установить направление протекания термодинамических процессов.
Второе начало термодинамикиопределяет направление протекания термодинамических процессов и тем самым дает ответ на вопрос, какие процессы в природе могут протекать самопроизвольно.
Некоторые из формулировок второго начала термодинамики:
· невозможен процесс, единственным результатом которого является превращение всей теплоты, полученной от некоторого тела, в эквивалентную ей работу.
· невозможен процесс, единственным результатом которого является передача энергии в окорме теплоты от менее нагретого тела к более нагретому телу.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Источник