Во сколько раз увеличится коэффициент полезного действия

6.3. Второй закон термодинамики
6.3.1. Коэффициент полезного действия тепловых двигателей. Цикл Карно
Второе начало термодинамики возникло из анализа работы тепловых двигателей (машин). В формулировке Кельвина оно выглядит следующим образом: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.
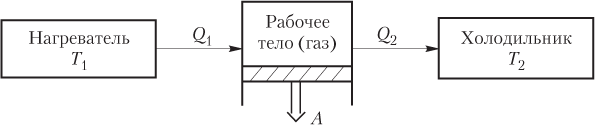
Схема действия тепловой машины (теплового двигателя) представлена на рис. 6.3.
Рис. 6.3
Цикл работы теплового двигателя состоит из трех этапов:
1) нагреватель передает газу количество теплоты Q
1;
2) газ, расширяясь, совершает работу A;
3) для возвращения газа в исходное состояние холодильнику передается теплота Q
2.
Из первого закона термодинамики для циклического процесса
Q = A,
где Q — количество теплоты, полученное газом за цикл, Q = Q
1 − Q
2; Q
1 — количество теплоты, переданное газу от нагревателя; Q
2 — количество теплоты, отданное газом холодильнику.
Поэтому для идеальной тепловой машины справедливо равенство
Q
1 − Q
2 = A.
Когда потери энергии (за счет трения и рассеяния ее в окружающую среду) отсутствуют, при работе тепловых машин выполняется закон сохранения энергии
Q
1 = A + Q
2,
где Q
1 — теплота, переданная от нагревателя рабочему телу (газу); A — работа, совершенная газом; Q
2 — теплота, переданная газом холодильнику.
Коэффициент полезного действия тепловой машины вычисляется по одной из формул:
η=AQ1⋅100 %, η=Q1−Q2Q1⋅100 %, η=(1−Q2Q1)⋅100 %,
где A — работа, совершенная газом; Q
1 — теплота, переданная от нагревателя рабочему телу (газу); Q
2 — теплота, переданная газом холодильнику.
Наиболее часто в тепловых машинах используется цикл Карно, так как он является самым экономичным.
Цикл Карно состоит из двух изотерм и двух адиабат, показанных на рис. 6.4.
Рис. 6.4
Участок 1–2 соответствует контакту рабочего вещества (газа) с нагревателем. При этом нагреватель передает газу теплоту Q
1 и происходит изотермическое расширение газа при температуре нагревателя T
1. Газ совершает положительную работу (A
12 > 0), его внутренняя энергия не изменяется (∆U
12 = 0).
Участок 2–3 соответствует адиабатному расширению газа. При этом теплообмена с внешней средой не происходит, совершаемая положительная работа A
23
приводит к уменьшению внутренней энергии газа: ∆U
23
= −A
23
, газ охлаждается до температуры холодильника T
2.
Участок 3–4 соответствует контакту рабочего вещества (газа) с холодильником. При этом холодильнику от газа поступает теплота Q
2 и происходит изотермическое сжатие газа при температуре холодильника T
2. Газ совершает отрицательную работу (A
34 < 0), его внутренняя энергия не изменяется (∆U
34 = 0).
Участок 4–1 соответствует адиабатному сжатию газа. При этом теплообмена с внешней средой не происходит, совершаемая отрицательная работа A
41
приводит к увеличению внутренней энергии газа: ∆U
41
= −A
41
, газ нагревается до температуры нагревателя T
1, т.е. возвращается в исходное состояние.
Коэффициент полезного действия тепловой машины, работающей по циклу Карно, вычисляется по одной из формул:
η=T1−T2T1⋅100 %, η=(1−T2T1)⋅100 %,
где T
1 — температура нагревателя; T
2 — температура холодильника.
Пример 9. Идеальная тепловая машина совершает за цикл работу 400 Дж. Какое количество теплоты передается при этом холодильнику, если коэффициент полезного действия машины равен 40 %?
Решение. Коэффициент полезного действия тепловой машины определяется формулой
η=AQ1⋅100 %,
где A — работа, совершаемая газом за цикл; Q
1 — количество теплоты, которое передается от нагревателя рабочему телу (газу).
Искомой величиной является количество теплоты Q
2, переданное от рабочего тела (газа) холодильнику, не входящее в записанную формулу.
Связь между работой A, теплотой Q
1, переданной от нагревателя газу, и искомой величиной Q
2 устанавливается с помощью закона сохранения энергии для идеальной тепловой машины
Q
1 = A + Q
2.
Уравнения образуют систему
η=AQ1⋅100 %,Q1=A+Q2,}
которую необходимо решить относительно Q
2.
Для этого исключим из системы Q
1, выразив из каждого уравнения
Q1=Aη⋅100 %,Q1=A+Q2}
и записав равенство правых частей полученных выражений:
Aη⋅100 %=A+Q2.
Искомая величина определяется равенством
Q2=Aη⋅100 %−A=A(100 %η−1).
Расчет дает значение:
Q2=400⋅(100 %40 %−1)=600 Дж.
Количество теплоты, переданной за цикл от газа холодильнику идеальной тепловой машины, составляет 600 Дж.
Пример 10. В идеальной тепловой машине от нагревателя к газу поступает 122 кДж/мин, а от газа холодильнику передается 30,5 кДж/мин. Вычислить коэффициент полезного действия данной идеальной тепловой машины.
Решение. Для расчета коэффициента полезного действия воспользуемся формулой
η=(1−Q2Q1)⋅100 %,
где Q
2 — количество теплоты, которое передается за цикл от газа холодильнику; Q
1 — количество теплоты, которое передается за цикл от нагревателя рабочему телу (газу).
Преобразуем формулу, выполнив деление числителя и знаменателя дроби на время t:
η=(1−Q2/tQ1/t)⋅100 %,
где Q
2/t — скорость передачи теплоты от газа холодильнику (количество теплоты, которое передается газом холодильнику в секунду); Q
1/t — скорость передачи теплоты от нагревателя рабочему телу (количество теплоты, которое передается от нагревателя газу в секунду).
В условии задачи скорость передачи теплоты задана в джоулях в минуту; переведем ее в джоули в секунду:
- от нагревателя газу —
Q1t=122 кДж/мин=122⋅10360 Дж/с;
- от газа холодильнику —
Q2t=30,5 кДж/мин=30,5⋅10360 Дж/с.
Рассчитаем коэффициент полезного действия данной идеальной тепловой машины:
η=(1−30,5⋅10360⋅60122⋅103)⋅100 %=75 %.
Пример 11. Коэффициент полезного действия тепловой машины, работающей по циклу Карно, равен 25 %. Во сколько раз увеличится коэффициент полезного действия, если температуру нагревателя увеличить, а температуру холодильника уменьшить на 20 %?
Решение. Коэффициент полезного действия идеальной тепловой машины, работающей по циклу Карно, определяется следующими формулами:
- до изменения температур нагревателя и холодильника —
η1=(1−T2T1)⋅100 %,
где T
1 — первоначальная температура нагревателя; T
2 — первоначальная температура холодильника;
- после изменения температур нагревателя и холодильника —
η2=(1−T′2T′1)⋅100 %,
где T′1 — новая температура нагревателя, T′1=1,2T1; T′2 — новая температура холодильника, T′2=0,8T2.
Уравнения для коэффициентов полезного действия образуют систему
η1=(1−T2T1)⋅100 %,η2=(1−0,8T21,2T1)⋅100 %,}
которую необходимо решить относительно η2.
Из первого уравнения системы с учетом значения η1 = 25 % найдем отношение температур
T2T1=1−η1100 %=1−25 %100 %=0,75
и подставим во второе уравнение
η2=(1−0,81,2⋅0,75)⋅100 %=50 %.
Искомое отношение коэффициентов полезного действия равно:
η2η1=50 %25 %=2,0.
Следовательно, указанное изменение температур нагревателя и холодильника тепловой машины приведет к увеличению коэффициента полезного действия в 2 раза.
Источник
В этой статье подробно разберем решение нескольких задач из разных разделов термодинамики.
Наш телеграм – это полезная информация для всех студентов каждый день, присоединяйтесь.
Задачи по термодинамике с решениями
Прежде чем начать, вспомним, какие задачи мы уже решали раньше:
- задачи на второе начало термодинамики;
- задачи на КПД теплового двигателя;
- задачи на работу в термодинамике;
- задачи по теме «Теплоемкость идеального газа»;
- задачи на расчет количества теплоты;
- задачи на внутреннюю энергию;
- задачи на первый закон термодинамики;
- задачи по молекулярно-кинетической теории.
Также напомним, что прежде чем начинать решать задачи, полезно ознакомиться с общей памяткой, а при решении держать под рукой полезные формулы.
Задача №1 на уравнение состояния газа
Условие
Кислород массой m=0.032кг находится в закрытом сосуде под давлением p=0,1МПа при температуре T=290К. После нагревания давление в сосуде повысилось в 4 раза. Определите: 1) объем сосуда; 2) температуру, до которой газ нагрели; 3) количество теплоты, сообщенное газу.
Решение
Запишем уравнение состояния газа и найдем объем:
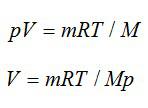
При изохорном процессе:
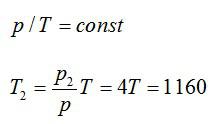
Сообщенное газу количество теплоты:

Зная, что для двухатомного кислорода число степеней свободы молекулы i=5, вычислим:

Ответ: 1) 24 л, 2) 1160 К, 3) 578.4 Дж.
Задача №2 на цикл Карно
Условие
Идеальный газ совершает цикл Карно при температурах нагревателя 400 К и холодильника 290 К. Во сколько раз увеличится коэффициент полезного действия цикла, если температура нагревателя возрастёт до 600 К?
Решение
Коэффициент полезного действия цикла Карно:

Коэффициенты полезного действия цикла Карно при разных температурах нагревателя соответственно:

Найдём отношение коэффициентов:

Следовательно, коэффициент полезного действия цикла Карно увеличится в 1,88 раза.
Ответ: КПД увеличивается в 1,88 раза.
Задача №3 на МКТ
Условие
В баллоне объёмом 0,05 м3 находится 0,12 кмоля газа при давлении 0,6∙10^7 Па. Определить среднюю кинетическую энергию поступательного движения молекулы газа.
Решение
Средняя кинетическая энергия поступательного движения:

где Т – термодинамическая температура идеального газа. Из уравнения Менделеева-Клапейрона найдем температуру:

Тогда:

Подставим значения и вычислим:

Ответ: 6,23*10^-21 Дж.
Задача №4 на внутреннюю энергию газа
Условие
Один моль одноатомного идеального газа изобарно расширяется от объема 5 литров до 10 литров при давлении в 202 кПа. Как изменилась внутренняя энергия газа в этом процессе?
Решение
Для одноатомного газа i=3. Для внутренней энергии идеального газа запишем, выражая температуру через уравнение Клапейрона-Менделеева:

Ответ: 1515 Дж
Задача №5 на изопроцессы
Условие
Кислород, занимающий при давлении р1 объем V1, расширяется в n раз. Определите конечное давление и работу, совершаемую газом. Рассмотрите следующие процессы:
- Изобарный.
- Изотермический.
- Адиабатный.
Решение
1) При изобарном процессе давление не меняется, работа газа:

2) при изотермическом процессе:

Работа газа:

3) уравнение адиабаты:

Ответ: см. выше
Вопросы по термодинамике
Вопрос 1. Сформулируйте первое начало термодинамики.
Ответ. Первое начало термодинамики гласит:
Теплота, полученная системой, идет на изменение ее внутренней энергии и на совершение системой работы против внешних сил.
В другой формулировке первое начало утверждает невозможность построения вечного двигателя первого рода.
Вопрос 2. Что такое идеальный газ?
Ответ. Идеальный газ – это математическая модель газа, в которой соударения между молекулами газа абсолютно упруги, между молекулами не действуют силы притяжения или отталкивания, потенциальной энергией взаимодействия молекул можно пренебречь.
В расширенной модели идеального газа его молекулы имеют сферическую форму
Вопрос 3. Что такое термодинамическая система?
Ответ. Термодинамическая система – это физическая система, состоящая из из большого количества частиц, способная обмениваться с окружающей средой энергией и веществом. Такую систему можно описать статистическими законами.
Вопрос 4. Сформулируйте второе начало термодинамики.
Ответ. У второго начало терможинами есть несколько формулировок. Вот одна из них:
Теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому.
Вопрос 5. Что такое теплоемкость?
Ответ. Теплоемкость – физическая величина, численно равная количеству теплоты, которое необходимо передать телу, чтобы увеличить его температуру на 1 градус.
Если у вас есть вопросы по термодинамике, на которые вы ищете ответы, оставляйте их в комментариях. А если не получается решить какую-то задачу, спросите у экспертов профессионального студенческого сервиса, они обязательно помогут.
Источник
300.Идеальный газ совершает цикл Карно при температурах теплоприемника Т2 = 290 К и теплоотдатчика Т1 = 400 К. Во сколько раз увеличится коэффициент полезного действия h цикла, если температура теплоотдатчика возрастет до Т/1 = 600 К?
301.Температура нагревателя тепловой машины, работающей по циклу Карно, 480 К, температура холодильника 390 К. Какой должна быть температура нагревателя при неизменной температуре холодильника, чтобы КПД машины увеличился в два раза?
302.Тепловая машина работает по циклу Карно, КПД которого 0,2. Каким будет КПД этой машины, если она совершит тот же цикл в обратном направлении?
303.Газ, совершающий цикл Карно, отдал теплоприемнику теплоту Q2 = 14 КДж. Определить температуру Т1 теплоотдатчика, если при температуре теплоприемника Т2= 280 К работа цикла А = 6 КДж.
304.Тепловая машина работает по циклу Карно, КПД которого 0,2. Каким будет КПД этой машины, если она совершит тот же цикл в обратном направлении?
305.Холодильная машина работает по обратному циклу Карно, КПД которого 200%. Каков будет КПД тепловой машины, работающей по прямому циклу Карно?
306.Температура нагревателя тепловой машины, работающей по циклу Карно, 500 К, температура холодильника 350 К. Какой должна быть температура нагревателя при неизменной температуре холодильника, чтобы КПД машины увеличился в два раза?
307.Тепловая машина работает по циклу Карно, КПД которого 0,15. Каким будет КПД этой машины, если она совершит тот же цикл в обратном направлении?
308.Холодильная машина работает по обратному циклу Карно, КПД которого 300%. Каков будет КПД тепловой машины, работающей по прямому циклу Карно?
309.Коэффициент полезного действия цикла Карно равен 0,3. При изотермическом расширении газ получил от нагревателя 200 Дж энергии. Определить работу, совершаемую при изотермическом сжатии.
310.Температура нагревателя в 3 раза выше температуры холодильника. Какую часть энергии, полученной в цикле Карно от нагревателя, газ отдает холодильнику?
311.При совершении цикла Карно газ получил от нагревателя 16,77 кДж энергии и совершил 5,59 кДж работы. Во сколько раз температура нагревателя выше температуры холодильника?
312.Газ совершает цикл Карно. Абсолютная температура холодильника 290 К. Во сколько раз увеличится КДД цикла, если температура нагревателя повысится от 400 К до 600 К?
313.Газ совершает цикл Карно. Работа изотермического расширения газа 5 Дж. Определить работу изотермического сжатия, если термический КПД цикла 0,2.
314.Найти КПД цикла, состоящего из двух изобар и двух адиабат, если температуры характерных точек равны 370 К, 600 К, 500 К и 350 К. Решение пояснить диаграммой P-V.
315.Совершая прямой цикл Карно, газ отдал холодильнику 25% теплоты, полученной от нагревателя. Определить температуру холодильника, если температура нагревателя 500 К.
316.Коэффициент полезного действия цикла Карно равен 0,25. При изотермическом расширении газ получил от нагревателя 250 Дж энергии. Определить работу, совершаемую при изотермическом сжатии.
317.Температура нагревателя в 3 раза выше температуры холодильника. Какую часть энергии, полученной в цикле Карно от нагревателя, газ отдает холодильнику?
318.При совершении цикла Карно газ получил от нагревателя 20 кДж энергии и совершил 5,5 кДж работы. Во сколько раз температура нагревателя выше температуры холодильника?
319.Газ совершает цикл Карно. Абсолютная температура холодильника 240 К. Во сколько раз увеличится КПД цикла, если температура нагревателя повысится от 370 К до 570 К?
320.Газ совершает цикл Карно. Работа изотермического расширения газа 7,5 Дж. Определить работу изотермического сжатия, если термический КПД цикла 0,15.
321.Найти КПД цикла, состоящего из двух изобар и двух адиабат, если температуры характерных точек равны 350 К, 550 К, 400 К и 320 К. Решение пояснить диаграммой P-V.
322.Совершая прямой цикл Карно, газ отдал холодильнику 20% теплоты, полученной от нагревателя. Определить температуру холодильника, если температура нагревателя 450 К.
323.Идеальный газ совершает цикл Карно. Температура нагревателя T1 = 500 К, холодильника Т2 = 300 К. Работа изотермического расширения газа составляет 2 кДж. Определите: 1) термический КПД цикла; 2) количество теплоты, отданное газом при изотермическом сжатии холодильнику.
Энтропия
324.Лед массой 0,2 литра, находящийся при температуре – 30°С, превращается в пар. Определить изменение энтропии.
325.Найти изменение энтропии 1 кг воздуха, если его давление увеличилось от 0,2 МПа до 1,0 МПа, а температура понизилась от 327°С до 127°С.
326.Определить изменение энтропии при изотермическом сжатии 1 моля кислорода от объема V до объема 1/3 V.
327.При изобарном расширении водорода массой 20 г его объем увеличивается в три раза. Определить изменение энтропии водорода при этом процессе.
328.Определить изменение энтропии, происходящее при смешивании 2 кг воды при температуре 250 К и 4 кг воды при температуре 300 К.
329.Объем гелия, масса которого 1 кг, увеличился в четыре раза: а) изотермически; б) адиабатно. Каково изменение энтропии в этих случаях?
330.Определить изменение энтропии 1 моль идеального газа при изохорном, изобарном и изотермическом процессах.
331.Определить изменение энтропии 2 кг расплавленного свинца при охлаждении его от 327°С до 10°С. Температура плавления свинца 327°С.
332.Найти изменение энтропии при нагревании 1 кг воды от 0°С до 100°С и последующем .превращении ее в пар при той же температуре.
333.Определить изменение энтропии при изобарном нагревании 0,1 кг азотаот17°Сдо97°С.
334.Найти изменение энтропии при нагревании и плавлении 1 кг олова. Первоначальная температура олова 25°С.
335.Определить изменение энтропии, происходящее при смешивании 2 кг воды при температуре 250 К и 4 кг воды при температуре 300 К.
336.Определить изменение энтропии 2 кг расплавленного свинца при охлаждении его от 327°С до 10°С. Температура плавления свинца 327°С.
337.Лед массой 0,2 литра, находящийся при температуре – 30°С, превращается в пар. Определить изменение энтропии.
338.Найти изменение энтропии 1,5 кг воздуха, если его давление увеличилось от 0,15 МПа до 0,5 МПа, а температура понизилась от 327°С до 127°С.
339.Определить изменение энтропии при изотермическом сжатии 1 моля кислорода от объема V до объема 1/3 V.
340.При изобарном расширении водорода массой 20 г его объем увеличивается в три раза. Определить изменение энтропии водорода при этом процессе.
341.Определить изменение энтропии, происходящее при смешивании 1,5 кг воды при температуре 270 К и 3 кг воды при температуре 300 К.
342.Объем гелия, масса которого 1 кг, увеличился в четыре раза: а) изотермически; б) адиабатно. Каково изменение энтропии в этих случаях?
343.Определить изменение энтропии 1 моль идеального газа при изохорном, изобарном и изотермическом процессах.
344.Определить изменение энтропии 1,5 кг расплавленного свинца при охлаждении его от 327°С до 10°С. Температура плавления свинца 327°С.
345.Найти изменение энтропии при нагревании 1 кг воды от 0°С до 100°С и последующем .превращении ее в пар при той же температуре.
346.Определить изменение энтропии при изобарном нагревании 0,1 кг азотаот17°Сдо97°С.
347.Найти изменение энтропии при нагревании и плавлении 1,5 кг олова. Первоначальная температура олова 20°С.
348.Определить изменение энтропии, происходящее при смешивании 2 кг воды при температуре 250 К и 4 кг воды при температуре 300 К.
349.Определить изменение энтропии 3 кг расплавленного свинца при охлаждении его от 327°С до 20°С. Температура плавления свинца 327°С.
Основные физические константы
| Гравитационная постоянная | G = 6.6720*10-11 Н*м2/кг2 |
| Скорость света в вакууме | c = 2.99792458*108 м/с |
| Магнитная постоянная | m0 = 1.25663706144*10-6 Гн/м |
| Электрическая постоянная | e0 = 8.85418782*10-12 Ф/м |
| Постоянная Планка | h = 6.626176*10-34 Дж*с |
| Масса покоя электрона | me = 9.109534*10-31 кг |
| Масса покоя протона | mp = 1.6726485*10-27 кг |
| Масса покоя нейтрона | mn = 1.6749543*10-27 кг |
| Заряд электрона | e = 1.6021892*10-19 Кл |
| Атомная единица массы | 1.660565*10-27 кг |
| Постоянная Авогадро | NA = 6.022045*1023 моль-1 |
| Постоянная Фарадея | F = 96484.56 Кл/моль |
| Молярная газовая постоянная | R = 8.31441 Дж/(моль*К) |
| Постоянная Больцмана | k = 1.380662*10-23 Дж/К |
| Нормальный (молярный) объем идеального газа при нормальных условиях | V0 = 2.241*10-2 м3/моль |
| Нормальное атмосферное давление | Pатм. = 101325 Па |
| Радиус первой боровской орбиты | a0 = 5.2917706*10-11 м |
| Ускорение свободного падения | g = 9.80665 м/с2 |
СПИСОК ЛИТЕРАТУРЫ
1. Трофимова Т.И. Курс физики: Учебное пособие для инженерно-технических специальностей вузов – М: Высшая школа, 2002, 540 с.
2. Трофимова Т. И. Сборник задач по курсу физики: Учеб. пособие для втузов – М.: Высшая школа. 302 с. 1996
3. Павлова З. Г., Трофимова Т. И. Сборник задач по курсу физики с решениями: Учеб. пособие для вузов, М.: Высшая школа 2001. 589 с.
Чертов А.Г., Воробьев А.А. Задачник по физике. М.: ФИЗМАТЛИТ. 2002.
Источник