Во сколько раз полезная работа совершенная двигателем

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: принципы действия тепловых машин, КПД тепловой машины, тепловые двигатели и охрана окружающей среды.
Коротко говоря, тепловые машины преобразуют теплоту в работу или, наоборот, работу в теплоту.
Тепловые машины бывают двух видов — в зависимости от направления протекающих в них процессов.
1. Тепловые двигатели преобразуют теплоту, поступающую от внешнего источника, в механическую работу.
2. Холодильные машины передают тепло от менее нагретого тела к более нагретому за счёт механической работы внешнего источника.
Рассмотрим эти виды тепловых машин более подробно.
Тепловые двигатели
Мы знаем, что совершение над телом работы есть один из способов изменения его внутренней энергии: совершённая работа как бы растворяется в теле, переходя в энергию беспорядочного движения и взаимодействия его частиц.

Рис. 1. Тепловой двигатель
Тепловой двигатель — это устройство, которое, наоборот, извлекает полезную работу из «хаотической» внутренней энергии тела. Изобретение теплового двигателя радикально изменило облик человеческой цивилизации.
Принципиальную схему теплового двигателя можно изобразить следующим образом (рис. 1). Давайте разбираться, что означают элементы данной схемы.
Рабочее тело двигателя — это газ. Он расширяется, двигает поршень и совершает тем самым полезную механическую работу.
Но чтобы заставить газ расширяться, преодолевая внешние силы, нужно нагреть его до температуры, которая существенно выше температуры окружающей среды. Для этого газ приводится в контакт с нагревателем — сгорающим топливом.
В процессе сгорания топлива выделяется значительная энергия, часть которой идёт на нагревание газа. Газ получает от нагревателя количество теплоты . Именно за счёт этого тепла двигатель совершает полезную работу .
Это всё понятно. Что такое холодильник и зачем он нужен?
При однократном расширении газа мы можем использовать поступающее тепло максимально эффективно и целиком превратить его в работу. Для этого надо расширять газ изотермически: первый закон термодинамики, как мы знаем, даёт нам в этом случае .
Но однократное расширение никому не нужно. Двигатель должен работать циклически, обеспечивая периодическую повторяемость движений поршня. Следовательно, по окончании расширения газ нужно сжимать, возвращая его в исходное состояние.
В процессе расширения газ совершает некоторую положительную работу . В процессе сжатия над газом совершается положительная работа (а сам газ совершает отрицательную работу ). В итоге полезная работа газа за цикл: .
Разумеется, должно быть , или (иначе никакого смысла в двигателе нет).
Сжимая газ, мы должны совершить меньшую работу, чем совершил газ при расширении.
Как этого достичь? Ответ: сжимать газ под меньшими давлениями, чем были в ходе расширения. Иными словами, на -диаграмме процесс сжатия должен идти ниже процесса расширения, т. е. цикл должен проходиться по часовой стрелке (рис. 2).

Рис. 2. Цикл теплового двигателя
Например, в цикле на рисунке работа газа при расширении равна площади криволинейной трапеции . Аналогично, работа газа при сжатии равна площади криволинейной трапеции со знаком минус. В результате работа газа за цикл оказывается положительной и равной площади цикла .
Хорошо, но как заставить газ возвращаться в исходное состояние по более низкой кривой, т. е. через состояния с меньшими давлениями? Вспомним, что при данном объёме давление газа тем меньше, чем ниже температура. Стало быть, при сжатии газ должен проходить состояния с меньшими температурами.
Вот именно для этого и нужен холодильник: чтобы охлаждать газ в процессе сжатия.
Холодильником может служить атмосфера (для двигателей внутреннего сгорания) или охлаждающая проточная вода (для паровых турбин). При охлаждении газ отдаёт холодильнику некоторое количество теплоты .
Суммарное количество теплоты, полученное газом за цикл, оказывается равным . Согласно первому закону термодинамики:
где — изменение внутренней энергии газа за цикл. Оно равно нулю: , так как газ вернулся в исходное состояние (а внутренняя энергия, как мы помним, является функцией состояния). В итоге работа газа за цикл получается равна:
(1)
Как видите, : не удаётся полностью превратить в работу поступающее от нагревателя тепло. Часть теплоты приходится отдавать холодильнику — для обеспечения цикличности процесса.
Показателем эффективности превращения энергии сгорающего топлива в механическую работу служит коэффициент полезного действия теплового двигателя.
КПД теплового двигателя — это отношение механической работы к количеству теплоты , поступившему от нагревателя:
С учётом соотношения (1) имеем также
(2)
КПД теплового двигателя, как видим, всегда меньше единицы. Например, КПД паровых турбин приблизительно , а КПД двигателей внутреннего сгорания около .
Холодильные машины
Житейский опыт и физические эксперименты говорят нам о том, что в процессе теплообмена теплота передаётся от более нагретого тела к менее нагретому, но не наоборот. Никогда не наблюдаются процессы, в которых за счёт теплообмена энергия самопроизвольно переходит от холодного тела к горячему, в результате чего холодное тело ещё больше остывало бы, а горячее тело — ещё больше нагревалось.

Рис. 3. Холодильная машина
Ключевое слово здесь — «самопроизвольно». Если использовать внешний источник энергии, то осуществить процесс передачи тепла от холодного тела к горячему оказывается вполне возможным. Это и делают холодильные
машины.
По сравнению с тепловым двигателем процессы в холодильной машине имеют противоположное направление (рис. 3).
Рабочее тело холодильной машины называют также хладагентом. Мы для простоты будем считать его газом, который поглощает теплоту при расширении и отдаёт при сжатии (в реальных холодильных установках хладагент — это летучий раствор с низкой температурой кипения, который забирает теплоту в процессе испарения и отдаёт при конденсации).
Холодильник в холодильной машине — это тело, от которого отводится теплота. Холодильник передаёт рабочему телу (газу) количество теплоты , в результате чего газ расширяется.
В ходе сжатия газ отдаёт теплоту более нагретому телу — нагревателю. Чтобы такая теплопередача осуществлялась, надо сжимать газ при более высоких температурах, чем были при расширении. Это возможно лишь за счёт работы , совершаемой внешним источником (например, электродвигателем (в реальных холодильных агрегатах электродвигатель создаёт в испарителе низкое давление, в результате чего хладагент вскипает и забирает тепло; наоборот, в конденсаторе электродвигатель создаёт высокое давление, под которым хладагент конденсируется и отдаёт тепло)). Поэтому количество теплоты, передаваемое нагревателю, оказывается больше количества теплоты, забираемого от холодильника, как раз на величину :
Таким образом, на -диаграмме рабочий цикл холодильной машины идёт против часовой стрелки. Площадь цикла — это работа , совершаемая внешним источником (рис. 4).

Рис. 4. Цикл холодильной машины
Основное назначение холодильной машины — охлаждение некоторого резервуара (например, морозильной камеры). В таком случае данный резервуар играет роль холодильника, а нагревателем служит окружающая среда — в неё рассеивается отводимое от резервуара тепло.
Показателем эффективности работы холодильной машины является холодильный коэффициент, равный отношению отведённого от холодильника тепла к работе внешнего источника:
Холодильный коэффициент может быть и больше единицы. В реальных холодильниках он принимает значения приблизительно от 1 до 3.
Имеется ещё одно интересное применение: холодильная машина может работать как тепловой насос. Тогда её назначение — нагревание некоторого резервуара (например, обогрев помещения) за счёт тепла, отводимого от окружающей среды. В данном случае этот резервуар будет нагревателем, а окружающая среда — холодильником.
Показателем эффективности работы теплового насоса служит отопительный коэффициент, равный отношению количества теплоты, переданного обогреваемому резервуару, к работе внешнего источника:
Значения отопительного коэффициента реальных тепловых насосов находятся обычно в диапазоне от 3 до 5.
Тепловая машина Карно
Важными характеристиками тепловой машины являются наибольшее и наименьшее значения температуры рабочего тела в ходе цикла. Эти значения называются соответственно температурой нагревателя и температурой холодильника.
Мы видели, что КПД теплового двигателя строго меньше единицы. Возникает естественный вопрос: каков наибольший возможный КПД теплового двигателя с фиксированными значениями температуры нагревателя и температуры холодильника ?
Пусть, например, максимальная температура рабочего тела двигателя равна , а минимальная — . Каков теоретический предел КПД такого двигателя?
Ответ на поставленный вопрос дал французский физик и инженер Сади Карно в 1824 году.
Он придумал и исследовал замечательную тепловую машину с идеальным газом в качестве рабочего тела. Эта машина работает по циклу Карно, состоящему из двух изотерм и двух адиабат.
Рассмотрим прямой цикл машины Карно, идущий по часовой стрелке (рис. 5). В этом случае машина функционирует как тепловой двигатель.

Рис. 5. Цикл Карно
Изотерма . На участке газ приводится в тепловой контакт с нагревателем температуры и расширяется изотермически. От нагревателя поступает количество теплоты и целиком превращается в работу на этом участке: .
Адиабата . В целях последующего сжатия нужно перевести газ в зону более низких температур. Для этого газ теплоизолируется, а затем расширяется адиабатно на учатке .
При расширении газ совершает положительную работу , и за счёт этого уменьшается его внутренняя энергия: .
Изотерма . Теплоизоляция снимается, газ приводится в тепловой контакт с холодильником температуры . Происходит изотермическое сжатие. Газ отдаёт холодильнику количество теплоты и совершает отрицательную работу .
Адиабата . Этот участок необходим для возврата газа в исходное состояние. В ходе адиабатного сжатия газ совершает отрицательную работу , а изменение внутренней энергии положительно: . Газ нагревается до исходной температуры .
Карно нашёл КПД этого цикла (вычисления, к сожалению, выходят за рамки школьной программы):
(3)
Кроме того, он доказал, что КПД цикла Карно является максимально возможным для всех тепловых двигателей с температурой нагревателя и температурой холодильника .
Так, в приведённом выше примере имеем:
В чём смысл использования именно изотерм и адиабат, а не каких-то других процессов?
Оказывается, изотермические и адиабатные процессы делают машину Карно обратимой. Её можно запустить по обратному циклу (против часовой стрелки) между теми же нагревателем и холодильником, не привлекая другие устройства. В таком случае машина Карно будет функционировать как холодильная машина.
Возможность запуска машины Карно в обоих направлениях играет очень большую роль в термодинамике. Например, данный факт служит звеном доказательства максимальности КПД цикла Карно. Мы ещё вернёмся к этому в следующей статье, посвящённой второму закону термодинамики.
Тепловые двигатели и охрана окружающей среды
Тепловые двигатели наносят серьёзный ущерб окружающей среде. Их повсеместное использование приводит к целому ряду негативных эффектов.
• Рассеяние в атмосферу огромного количества тепловой энергии приводит к повышению температуры на планете. Потепление климата грозит обернуться таянием ледников и катастрофическими бедствиями.
• К потеплению климата ведёт также накопление в атмосфере углекислого газа, который замедляет уход теплового излучения Земли в космос (парниковый эффект).
• Из-за высокой концентрации продуктов сгорания топлива ухудшается экологическая ситуация.
Это — проблемы в масштабе всей цивилизации. Для борьбы с вредными последствиями работы тепловых двигателей следует повышать их КПД, снижать выбросы токсичных веществ, разрабатывать новые виды топлива и экономно расходовать энергию.
Источник
6.3. Второй закон термодинамики
6.3.1. Коэффициент полезного действия тепловых двигателей. Цикл Карно
Второе начало термодинамики возникло из анализа работы тепловых двигателей (машин). В формулировке Кельвина оно выглядит следующим образом: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.
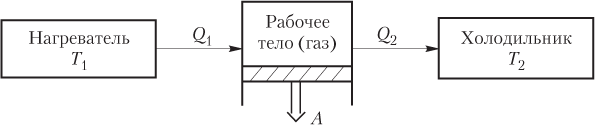
Схема действия тепловой машины (теплового двигателя) представлена на рис. 6.3.
Рис. 6.3
Цикл работы теплового двигателя состоит из трех этапов:
1) нагреватель передает газу количество теплоты Q
1;
2) газ, расширяясь, совершает работу A;
3) для возвращения газа в исходное состояние холодильнику передается теплота Q
2.
Из первого закона термодинамики для циклического процесса
Q = A,
где Q — количество теплоты, полученное газом за цикл, Q = Q
1 − Q
2; Q
1 — количество теплоты, переданное газу от нагревателя; Q
2 — количество теплоты, отданное газом холодильнику.
Поэтому для идеальной тепловой машины справедливо равенство
Q
1 − Q
2 = A.
Когда потери энергии (за счет трения и рассеяния ее в окружающую среду) отсутствуют, при работе тепловых машин выполняется закон сохранения энергии
Q
1 = A + Q
2,
где Q
1 — теплота, переданная от нагревателя рабочему телу (газу); A — работа, совершенная газом; Q
2 — теплота, переданная газом холодильнику.
Коэффициент полезного действия тепловой машины вычисляется по одной из формул:
η=AQ1⋅100 %, η=Q1−Q2Q1⋅100 %, η=(1−Q2Q1)⋅100 %,
где A — работа, совершенная газом; Q
1 — теплота, переданная от нагревателя рабочему телу (газу); Q
2 — теплота, переданная газом холодильнику.
Наиболее часто в тепловых машинах используется цикл Карно, так как он является самым экономичным.
Цикл Карно состоит из двух изотерм и двух адиабат, показанных на рис. 6.4.
Рис. 6.4
Участок 1–2 соответствует контакту рабочего вещества (газа) с нагревателем. При этом нагреватель передает газу теплоту Q
1 и происходит изотермическое расширение газа при температуре нагревателя T
1. Газ совершает положительную работу (A
12 > 0), его внутренняя энергия не изменяется (∆U
12 = 0).
Участок 2–3 соответствует адиабатному расширению газа. При этом теплообмена с внешней средой не происходит, совершаемая положительная работа A
23
приводит к уменьшению внутренней энергии газа: ∆U
23
= −A
23
, газ охлаждается до температуры холодильника T
2.
Участок 3–4 соответствует контакту рабочего вещества (газа) с холодильником. При этом холодильнику от газа поступает теплота Q
2 и происходит изотермическое сжатие газа при температуре холодильника T
2. Газ совершает отрицательную работу (A
34 < 0), его внутренняя энергия не изменяется (∆U
34 = 0).
Участок 4–1 соответствует адиабатному сжатию газа. При этом теплообмена с внешней средой не происходит, совершаемая отрицательная работа A
41
приводит к увеличению внутренней энергии газа: ∆U
41
= −A
41
, газ нагревается до температуры нагревателя T
1, т.е. возвращается в исходное состояние.
Коэффициент полезного действия тепловой машины, работающей по циклу Карно, вычисляется по одной из формул:
η=T1−T2T1⋅100 %, η=(1−T2T1)⋅100 %,
где T
1 — температура нагревателя; T
2 — температура холодильника.
Пример 9. Идеальная тепловая машина совершает за цикл работу 400 Дж. Какое количество теплоты передается при этом холодильнику, если коэффициент полезного действия машины равен 40 %?
Решение. Коэффициент полезного действия тепловой машины определяется формулой
η=AQ1⋅100 %,
где A — работа, совершаемая газом за цикл; Q
1 — количество теплоты, которое передается от нагревателя рабочему телу (газу).
Искомой величиной является количество теплоты Q
2, переданное от рабочего тела (газа) холодильнику, не входящее в записанную формулу.
Связь между работой A, теплотой Q
1, переданной от нагревателя газу, и искомой величиной Q
2 устанавливается с помощью закона сохранения энергии для идеальной тепловой машины
Q
1 = A + Q
2.
Уравнения образуют систему
η=AQ1⋅100 %,Q1=A+Q2,}
которую необходимо решить относительно Q
2.
Для этого исключим из системы Q
1, выразив из каждого уравнения
Q1=Aη⋅100 %,Q1=A+Q2}
и записав равенство правых частей полученных выражений:
Aη⋅100 %=A+Q2.
Искомая величина определяется равенством
Q2=Aη⋅100 %−A=A(100 %η−1).
Расчет дает значение:
Q2=400⋅(100 %40 %−1)=600 Дж.
Количество теплоты, переданной за цикл от газа холодильнику идеальной тепловой машины, составляет 600 Дж.
Пример 10. В идеальной тепловой машине от нагревателя к газу поступает 122 кДж/мин, а от газа холодильнику передается 30,5 кДж/мин. Вычислить коэффициент полезного действия данной идеальной тепловой машины.
Решение. Для расчета коэффициента полезного действия воспользуемся формулой
η=(1−Q2Q1)⋅100 %,
где Q
2 — количество теплоты, которое передается за цикл от газа холодильнику; Q
1 — количество теплоты, которое передается за цикл от нагревателя рабочему телу (газу).
Преобразуем формулу, выполнив деление числителя и знаменателя дроби на время t:
η=(1−Q2/tQ1/t)⋅100 %,
где Q
2/t — скорость передачи теплоты от газа холодильнику (количество теплоты, которое передается газом холодильнику в секунду); Q
1/t — скорость передачи теплоты от нагревателя рабочему телу (количество теплоты, которое передается от нагревателя газу в секунду).
В условии задачи скорость передачи теплоты задана в джоулях в минуту; переведем ее в джоули в секунду:
- от нагревателя газу —
Q1t=122 кДж/мин=122⋅10360 Дж/с;
- от газа холодильнику —
Q2t=30,5 кДж/мин=30,5⋅10360 Дж/с.
Рассчитаем коэффициент полезного действия данной идеальной тепловой машины:
η=(1−30,5⋅10360⋅60122⋅103)⋅100 %=75 %.
Пример 11. Коэффициент полезного действия тепловой машины, работающей по циклу Карно, равен 25 %. Во сколько раз увеличится коэффициент полезного действия, если температуру нагревателя увеличить, а температуру холодильника уменьшить на 20 %?
Решение. Коэффициент полезного действия идеальной тепловой машины, работающей по циклу Карно, определяется следующими формулами:
- до изменения температур нагревателя и холодильника —
η1=(1−T2T1)⋅100 %,
где T
1 — первоначальная температура нагревателя; T
2 — первоначальная температура холодильника;
- после изменения температур нагревателя и холодильника —
η2=(1−T′2T′1)⋅100 %,
где T′1 — новая температура нагревателя, T′1=1,2T1; T′2 — новая температура холодильника, T′2=0,8T2.
Уравнения для коэффициентов полезного действия образуют систему
η1=(1−T2T1)⋅100 %,η2=(1−0,8T21,2T1)⋅100 %,}
которую необходимо решить относительно η2.
Из первого уравнения системы с учетом значения η1 = 25 % найдем отношение температур
T2T1=1−η1100 %=1−25 %100 %=0,75
и подставим во второе уравнение
η2=(1−0,81,2⋅0,75)⋅100 %=50 %.
Искомое отношение коэффициентов полезного действия равно:
η2η1=50 %25 %=2,0.
Следовательно, указанное изменение температур нагревателя и холодильника тепловой машины приведет к увеличению коэффициента полезного действия в 2 раза.
Источник