Термический коэффициент полезного действия может быть

ТЕРМИЧЕСКИЙ КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
(Thermal efficiency) — отношение количества тепла, превращенного при данном термическом процессе в полезную механическую работу, к полному количеству тепла, затраченному в процессе.
Самойлов К. И.
Морской словарь. – М.-Л.: Государственное Военно-морское Издательство НКВМФ Союза ССР,
1941
.
Смотреть что такое “ТЕРМИЧЕСКИЙ КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ” в других словарях:
термический коэффициент полезного действия — тепловой коэффициент полезного действия термический КПД тепловой КПД — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом Синонимы тепловой коэффициент полезного действиятермический КПДтепловой КПД EN … Справочник технического переводчика
термический коэффициент полезного действия — šiluminio naudingumo koeficientas statusas T sritis Energetika apibrėžtis Nedimensinis dydis, apibūdinantis šiluminių variklių, verčiančių šilumą darbu, efektyvumą. Tai naudingo darbo, atlikto vieno ciklo metu, ir to paties ciklo metu darbinei… … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas
термический коэффициент полезного действия термодинамического цикла — Отношение работы, совершенной в прямом обратимом термодинамическом цикле, к теплоте, сообщенной рабочему телу от внешних источников. [Сборник рекомендуемых терминов. Выпуск 103. Термодинамика. Академия наук СССР. Комитет научно технической… … Справочник технического переводчика
термический коэффициент полезного действия термодинамического цикла — Отношение работы, совершенной в прямом обратимом термодинамическом цикле, к теплоте, сообщенной рабочему телу от внешних источников … Политехнический терминологический толковый словарь
термический коэффициент полезного действия цикла — Отношение работы, полученной в результате осуществления прямого обратимого цикла, к теплоте, подведенной к рабочему телу от теплоотдатчика … Политехнический терминологический толковый словарь
термический — ая, ое. thermique adj., нем. thermisch <гр. therme тепло. Связанный с теплотой, с применением тепловой энергии; тепловой. Термический режим поверхности земли. БАС 1. Термические ощущения у нас и у китайцев вероятно не вполне совпадают .. мы.… … Исторический словарь галлицизмов русского языка
ТЕРМИЧЕСКИЙ — ТЕРМИЧЕСКИЙ, термическая, термическое (от греч. thermos горячий) (спец.). прил., по знач. связанное с учением о теплоте и с применением тепловой энергии в технике. Термическая обработка металлов. Термический коэффициент полезного действия.… … Толковый словарь Ушакова
ТУРБИНЫ С ЗУБЧАТОЙ ПЕРЕДАЧЕЙ — (Geared turbine) турбозубчатая передача применяется в настоящее время на большинстве военных кораблей с мощными силовыми установками с целью уменьшить число оборотов турбины и получить наиболее выгодное число оборотов винта. Применение зубчатых… … Морской словарь
Атомный реактор с твёрдым теплоносителем — Атомный реактор с твёрдым теплоносителем ядерный реактор, рабочим телом теплоносителя которого, вместо воды, является материал на основе пиролитического углерода. Концепция Если рассматривать ядерные реакторы как основной источник… … Википедия
Ядерный реактор с твёрдым теплоносителем — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете … Википедия
Источник
В процессе расширения газ производит работу против сил внешнего давления. Для того чтобы вновь повторить тот же процесс расширения газа и вновь получить работу , нужно возвратить газ в исходное состояние т.е. сжать газ. При этом газ совершит круговой процесс (цикл). На сжатие газа, естественно, должна быть затрачена работа; эта работа подводится к газу от какого-либо внешнего источника.
Понятно, что процесс сжатия газа от давления p2 до давления p1 нужно осуществить по пути, отличному от пути процесса расширения. В противном случае работа, получаемая при расширении газа, будет равна работе, затрачиваемой на сжатие, и суммарная работа, полученная в результате кругового процесса, будет равна нулю. Работа, отдаваемая системой за один цикл (будем называть ее работой цикла), равна разности (алгебраической сумме) работы расширения и работы сжатия. Понятно, что путь процесса сжатия следует выбрать таким образом, чтобы работа сжатия по абсолютной величине была меньше работы расширения, иначе работа цикла будет отрицательной, т.е. в результате цикла работа будет не производиться, а затрачиваться; впрочем, как будет показано в дальнейшем, в определенных случаях (циклы холодильных машин) используется именно такое построение цикла.
Циклические процессы, в результате которых производится работа, осуществляются в различных тепловых двигателях. Тепловым двигателем называют непрерывно действующую систему, осуществляющую круговые процессы (циклы), в которых теплота превращается в работу. Вещество, за счет изменения состояния которого получают работу в цикле, именуется рабочим телом.
Типовой процесс в pV координатах.
Работа цикла находит очень удобную графическую интерпретацию в p, V-диаграмме.
Если 1-а-2 — кривая процесса расширения, а 2-b-1 — кривая процесса сжатия, то площадь под кривой 1-а-2 равна работе расширения, площадь под кривой 2-b-1 — работе сжатия, а площадь, ограниченная замкнутой кривой (кривой цикла) 1-a-2-b-1, представляет собой работу цикла.
Работа цикла Lц равна количеству теплоты, подведенной извне к рабочему телу. В соответствии с первым законом термодинамики: работа, производимая двигателем, строго равна количеству теплоты, отобранной от внешнего источника и подведенной к рабочему телу двигателя. Если бы можно было построить такой тепловой двигатель, в котором количество производимой работы было больше, чем количество теплоты, подведенной к рабочему телу от внешнего источника, то это означало бы, что первый закон термодинамики (закон сохранения и превращения энергии) несправедлив. Из этого следовало бы, что можно построить такой тепловой двигатель, в котором работа производилась бы вообще без подвода теплоты извне, т.е. вечный двигатель.
Что касается теплоты Qц, которая превращается в работу, то следует отметить, что на одних участках цикла теплота к рабочему телу подводится, на других — отводится. Как будет показано далее, отвод определенного количества теплоты от рабочего тела на некоторых участках цикла является неотъемлемым условием осуществимости цикла любого теплового двигателя.
Если обозначить теплоту, подводимую к рабочему телу в цикле, через Q1, а теплоту, отводимую от рабочего тела в цикле, через Q2, то очевидно, что
И тогда в соответствии с первым законом термодинамики:
Введем новое понятие о так называемом термическом коэффициенте полезного действия (КПД) цикла. Термическим КПД цикла называют отношение работы цикла к количеству теплоты, подведенной к рабочему телу в цикле. Обозначая термический КПД цикла ηт, получаем в соответствии с этим определением:
Термический КПД цикла характеризует степень совершенства того или иного цикла: чем больше ηт, тем совершеннее цикл; при подводе к рабочему телу одного и того же количества теплоты Q1 в цикле, у которого ηт больше, производится большая ′ работа Lц.
Введем понятие об источниках теплоты. Систему, от которой отбирается теплота Q1, сообщаемая рабочему телу цикла, принято называть горячим источником теплоты , а систему, которой отдается теплота Q2, отбираемая от рабочего тела, холодным источником теплоты.
Спасибо за прочтение материала. В следующий раз материал про будет про обратимые и необратимые циклы, которые приведут нас к формулировке второго закона термодинамики.
Источник
В качестве количественной характеристики термодинамической эффективности любого теплового двигателя используется так называемый термический коэффициент полезного действия(термический КПД) , определяемый отношением полезной работы, полученной в двигателе за цикл, к затраченному теплу от верхнего источника за этот же цикл, т.е. по определению
(4.3)
Первое начало термодинамики в применении к циклам тепловых машин (4.2) в формулировке В.Томсона даёт
(4.4)
причём следует иметь в виду, что здесь под понимается теплота, отнятая от верхнего источника тепла и переданная рабочему телу, т.е. по отношению к рабочему телу эта теплота положительна в соответствии с выбором знака теплоты. Величина же есть теплота, отданная рабочим телом нижнему источнику тепла, и по отношению отношению к рабочему телу эта теплота отрицательна, т.е., строго говоря, в применении к рабочему телу (4.4) должно быть записано в виде
(4.5)
Тогда выражение для термического КПД принимает вид
(4.6)
| Р5.Т3 | Формулировки II начала термодинамики | 0.3 часа |
После того как отказались от попыток построить вечный двигатель I рода, появились проекты тепловых двигателей, которые, по замыслу изобретателей, могли бы полностью превращать теплоту какого-либо источника тепла Q1 в полезную работу Lo. В частности, можно вообразить гипотетический тепловой двигатель, который бы производил полезную работу за счёт отнятия тепла от океанской воды. Легко подсчитать, что в этом случае охлаждение вод Мирового океана всего на 1оС дало бы количество энергии, которой хватило бы человечеству примерно на один миллион лет при современных темпах её потребления. Такой практически вечный двигатель, который полностью превращал бы теплоту источника в полезную работу, получил название вечного двигателя второго рода. Многочисленные попытки построить такой двигатель оказались безуспешными. Этот факт, не противоречащий I началу термодинамики, т.е. закону сохранения энергии, был возведён В.Томсоном (лордом Кельвином) в ранг закона, получившего название второго начала термодинамики. Итак, в формулировке Томсона второе начало термодинамики гласит: вечный двигатель второго рода невозможен.
Кроме этого немецким учёным Рудольфом Клаузиусом была дана другая формулировка второго начала термодинамики, которая гласит: теплота может самопроизвольно переходить только от тел с бòльшей температурой к телам с меньшей температурой; обратный переход невозможен без компенсации, т.е. без затраты внешней работы. Мы увидим в дальнейшем, что эти две формулировки (Томсона и Клаузиуса) эквивалентны, т.е. если предположить нарушение одной из них, то будет нарушена другая.
Замечание. Известно около двух десятков формулировок второго начала термодинамики, каждая из которых акцентирует внимание на том или ином аспекте проблемы превращения теплоты в работу, однако все они эквивалентны, т.е. являются логическим следствием какой-либо одной из них.
Формулировка Клаузиуса указывает на несимметрию процессов в макроскопической природе, на их необратимость. Наиболее распространёнными необратимыми процессами являются процессы теплообмена при конечной разности температур, трение при относительном движении соприкасающихся твёрдых тел, вязкое трение, т.е. внутреннее трение при движении жидкости или газа с неоднородным распределением скоростей, большинство химических реакций, диффузия и т.д. Все эти необратимые процессы сопровождаются диссипацией энергии, её рассеянием, так называемой “деградацией” энергии, т.е. переходом упорядоченной формы движения в неупорядоченную, хаотическую форму движения молекул и других структурных единиц макроскопических тел.
Итак, первый закон термодинамики даёт следующее ограничение для термического КПД тепловых двигателей
в то время как второе начало в формулировке Томсона накладывает более жёсткое ограничение
т.е. термический КПД любого теплового двигателя строго меньше единицы, поскольку теплота, передаваемая нижнему источнику тепла (теплоприёмнику), никогда не равна нулю.
Источник
В качестве количественной характеристики термодинамической эффективности любого теплового двигателя используется так называемый термический коэффициент полезного действия(термический КПД) , определяемый отношением полезной работы, полученной в двигателе за цикл, к затраченному теплу от верхнего источника за этот же цикл, т.е. по определению
(4.3)
Первое начало термодинамики в применении к циклам тепловых машин (4.2) в формулировке В.Томсона даёт
(4.4)
причём следует иметь в виду, что здесь под понимается теплота, отнятая от верхнего источника тепла и переданная рабочему телу, т.е. по отношению к рабочему телу эта теплота положительна в соответствии с выбором знака теплоты. Величина же есть теплота, отданная рабочим телом нижнему источнику тепла, и по отношению к рабочему телу эта теплота отрицательна, т.е., строго говоря, в применении к рабочему телу (4.4) должно быть записано в виде
(4.5)
Тогда выражение для термического КПД принимает вид
(4.6)
Итак, первый закон термодинамики даёт следующее ограничение для термического КПД тепловых двигателей
(4.7)
в то время как второе начало в формулировке Томсона накладывает более жёсткое ограничение
(4.8)
т.е. термический КПД любого теплового двигателя строго меньше единицы, поскольку теплота, передаваемая нижнему источнику тепла (теплоприёмнику), никогда не равна нулю.
В связи с этим возникает весьма важный с теоретической и практической точек зрения вопрос о нахождении максимально возможного термического КПД тепловой машины, работающей при наличии двух источников тепла (теплоотдатчика и теплоприёмника), и о принципах её конструирования. Эта проблема была решена в 1824 году французским инженером Сади Карно в опубликованной им работе “Размышления о движущей силе огня и о машинах, способных развить эту силу”.
Цикл Карно
В своём знаменитом сочинении Сади Карно обсудил принципы и предложил конструкцию теплового двигателя, который, по его мнению, должен обладать максимальной эффективностью преобразования теплоты в полезную работу. В современном изложении его рассуждения сводятся к следующему: в идеальной тепловой машине все необратимости должны быть сведены к минимуму, т.е. исключены. Это возможно, если все трущиеся поверхности идеально смазаны, скорости движения рабочего тела настолько малы, что можно пренебречь внутренним трением (вязкостью), химические реакции отсутствуют, передача тепла от верхнего источника рабочему телу происходит при температуре рабочего тела мèньшей, но бесконечно близкой к температуре источника тепла, а передача тепла от рабочего тела к теплоприёмнику происходит при температуре рабочего тела бòльшей, но бесконечно близкой к температуре нижнего источника тепла. Очевидно, что изменение температуры рабочего тела, для исключения необратимого теплообмена, должно происходить только адиабатически. Таким образом, приходим к идеальному циклу тепловой машины, работающей между двумя источниками тепла (теплоотдатчиком и теплоприёмником), известному под названием цикла Карнои состоящему из двух изотерм подвода и отвода тепла и двух адиабат. Относительно цикла Карно формулируются два утверждения, называемые теоремами Карно:
I теорема Карно – термический КПД цикла Карно максимален по сравнению с термическим КПД любой другой тепловой машины, работающей в том же интервале температур; это следует из того, что все процессы в машине Карно обратимы, т.е. в ней отсутствует диссипация энергии.
II теорема Карно– термический КПД цикла Карно не зависит от свойств рабочего тела, а зависит только от значений температур верхнего и нижнего источников тепла. Мы не будем подробно доказывать эту теорему, укажем лишь, что если бы КПД цикла Карно зависел от свойств рабочего тела, то можно было бы передавать тепло от холодного тела к более нагретому без затраты внешней работы, т.е. нарушался бы второй закон термодинамики в формулировке Клаузиуса.
Источник
Степень совершенства преобразования
теплоты в механическую работу в
термодинамическом цикле оценивается
термическим коэффициентом полезного
действия (к.п.д.). Термическим к. п. д.
термодинамического цикла называется
отношение работы, совершенной в прямом
обратимом термодинамическом цикле, к
теплоте, сообщенной рабочему телу от
внешних источников:
| (5.1) |
где q1– тепло отданное в
цикле рабочему телу теплоотдатчиком;q2– тепло отданное в цикле
рабочим телом теплоприёмнику;q1-q2– тепло, преобразованное в цикле в
механическую работуl.
Термический к. п. д. термодинамического
цикла показывает, какое количество
получаемой теплоты машина превращает
в работу в конкретных условиях протекания
идеального цикла. Чем больше величина
ηt, тем совершеннее цикл
и тепловая машина. Значение термического
к. п. д. термодинамического цикла всегда
меньше единицы.
5.5.Аналитическое выражение второго закона термодинамики
5.5.1.Цикл Карно
В 1824 г. С.Карно впервые рассмотрел
обратимый термодинамический цикл,
состоящий из двух изотерм и двух адиабат.
Этот цикл представляет собой замкнутый
процесс, совершаемый рабочим телом в
идеальной тепловой машине при наличии
двух истопников теплоты: нагревателя
(горячего источника) с температурой T1и холодильника (холодного источника) с
температуройT2Цикл Карно
вpv-диаграмме изображен на рис. 5.3.
|
Рис. 5.3. Прямой |
Процессы 1—2 и 3—4 являются
изотермическими, а 2—3 и 4—1 — адиабатными.
Начальная температура рабочего тела в
цикле принимается равной температуре
нагревателяT1. При
изотермическом расширении от состояния
1 до состояния 2 рабочее тело получает
от нагревателя количество теплотыq1при температуреT1. На
участке 2—3 рабочее тело адиабатно
расширяется. При этом температура
рабочего тела понижается отT1доT2, а давление падает отp2доp3. При
сжатии по изотерме 3—4 от рабочего тела
отводится к холодильнику количество
теплотыq2при температуреT2. Дальнейшее сжатие по
адиабате 4—1 приводит к повышению
температуры рабочего тела отT2доT1, а рабочее тело
возвращается в первоначальное состояние.
Суммарная работа цикла lцграфически изображается площадью 12341.
Термический к. п. д. цикла
| (5.2) |
Количество теплоты q1иq2определим из уравнений
|
|
Подставляя полученные значения q1иq2в уравнение (5.2), находим
| (5.3) |
Покажем, что
| (5.4) |
Для адиабатных процессов расширения
2—3 и сжатия 4—1 соответственно имеем
| и |
|
откуда
| или |
|
С учетом соотношения (5.4) уравнение (5.3)
принимает вид
| (5.5) |
Из уравнения (5.5) следует:
1. Термический к. п. д. цикла Карно зависит
только от абсолютных температур
нагревателя T1и холодильникаT2. Он возрастает с увеличением
температурыT1и уменьшениемT2, то есть чем больше
разность температурT1—T2,
тем выше к. п. д. цикла Карно.
2. Термический к. п. д. цикла Карно всегда
меньше единицы. Равенство ηt=1возможно только приT2=ОилиT1=∞, что практически
невозможно реализовать.
Теплота q1, подводимая к
рабочему телу в цикле Карно, не может
быть полностью превращена в работу,
значительное количество теплоты
отводится к теплоприемнику.
3. Термический к. п. д. цикла Карно при
T1=T2равен
нулю, таким образом, невозможно превращение
теплоты в работу, если все тела системы
имеют одинаковую температуру, то есть
находятся между собой в тепловом
равновесии.
4. Термический к. п. д. цикла Карно не
зависит от устройства двигателя и
физических свойств рабочего тела, а
зависит лишь от температур нагревателя
T1и холодильникаT2.
Это положение известно под названием
теоремы Карно. Последнее следует из
того, что формула (5.5) не содержит величин,
характеризующих свойства рабочего
тела.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник

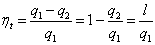 ,
,
 .
.
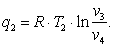



 ,
,
