Термический коэффициент полезного действия для кругового процесса формула
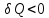
В
результате кругового процесса система
возвращается в исходное состояние,
следовательно, полное изменение
внутренней энергии равно нулю. Поэтому,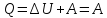
т.е. работа, совершаемая за цикл, равна
количеству полученной извне теплоты.
Если в ходе кругового процесса система
не только получает количество теплоты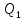
,
но и теряет (отдает) количество теплоты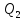
,
то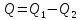
.
Термический
коэффициент полезного действия для
кругового процесса – это величина,
равная отношению работы, совершенной
системой, к количеству теплоты, полученному
в этом цикле системой:
.
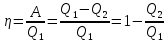(40.1)
§ 41. Энтропия
«Энтропия»
в переводе с греческого означает поворот,
превращение. Это понятие введено в
термодинамику немецким ученым Р.
Клаузиусом как мера необратимого
рассеяния энергии.
Количество
теплоты
,
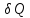которое должно быть доставлено системе
или отнято у неё при переходе от одного
состояния в другое, не определяется
однозначно начальным и конечным
состояниями, но существенно зависит от
способа осуществления этого перехода
.
Однако,
приведенное количество теплоты –
отношение теплоты
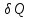к температуре
Т
системы при бесконечно малых изменениях
состояния системы – есть функция
состояния системы.
В любом
обратимом круговом процессе
.
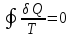Следовательно, подынтегральное выражение
есть полный дифференциал некоторой
функции, которая определяется только
начальным и конечным состояниями системы
и не зависит от пути, каким система
пришла в это состояние.
Энтропией
Sназывается
функция состояния системы, дифференциалом
которой является
:
.
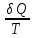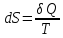(41.1)
Таким
образом, первое начало термодинамики
можно записать в виде
,
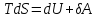откуда
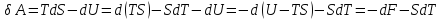
Функция
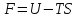является функцией состояния системы и
называется энергией Гельмгольца или
свободной энергией.
Изменение
энтропии.
В
замкнутой системе для обратимых процессов
;
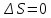для необратимых процессов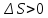
.
Энтропия
замкнутой системы может либо возрастать
(в случае необратимых процессов) либо
оставаться постоянной (в случае обратимых
процессов):
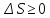
– неравенство
Клаузиуса.
Поскольку
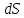и
и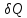меют один и тот же знак, то по характеру
изменения энтропии можно судить о
направлении процесса теплообмена.
При
нагревании тела
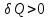и его энтропия возрастает
,
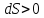при охлаждении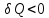и энтропия убывает
.
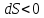Принцип
возрастания энтропии:Все
процессы в замкнутой системе ведут к
увеличению её энтропии. В замкнутой
системе идут в направлении от менее
вероятных состояний к более вероятным,
до тех пор, пока вероятность состояния
не станет максимальной. В состоянии
равновесия – наиболее вероятного
состояния системы- число микросостояний
максимально, при этом максимальна и
энтропия.
§ 42. Второе начало термодинамики
Выражая
всеобщий закон сохранения и превращения
энергии, первое начало термодинамики
не позволяет определить направление
протекания процесса. В самом деле,
процесс самопроизвольной передачи
энергии в форме теплоты от холодного
тела к горячему, ни в какой мере не
противоречит первому закону термодинамики.
Однако при опускании раскаленного куска
железа в холодную воду никогда не
наблюдается явление дальнейшего
нагревания железа за счет соответствующего
охлаждения воды. Далее, первое начало
не исключает возможности такого процесса,
единственным результатом которого было
бы превращение теплоты, полученной от
нагревателя в эквивалентную ей работу.
Так, например, основываясь на первом
начале можно было бы попытаться построить
периодически действующий двигатель,
совершающий работу за счет одного
источника тепла (например, за счет
внутренней энергии океана). Такой
двигатель называется вечным двигателем
второго рода. Обобщение огромного
экспериментального материала привело
к выводу о невозможности построения
вечного двигателя второго рода. Этот
вывод получил название второго начала
термодинамики.
Существует
ряд различных по форме, одинаковых по
существу формулировок второго начала:
Невозможен
процесс, единственным результатом
которого является превращение всей
теплоты, полученной от нагревателя, в
эквивалентную ей работу.Формулировка
Клаузиуса: теплота сама собой не может
переходить от менее нагретого тела к
более нагретому.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В процессе расширения газ производит работу против сил внешнего давления. Для того чтобы вновь повторить тот же процесс расширения газа и вновь получить работу , нужно возвратить газ в исходное состояние т.е. сжать газ. При этом газ совершит круговой процесс (цикл). На сжатие газа, естественно, должна быть затрачена работа; эта работа подводится к газу от какого-либо внешнего источника.
Понятно, что процесс сжатия газа от давления p2 до давления p1 нужно осуществить по пути, отличному от пути процесса расширения. В противном случае работа, получаемая при расширении газа, будет равна работе, затрачиваемой на сжатие, и суммарная работа, полученная в результате кругового процесса, будет равна нулю. Работа, отдаваемая системой за один цикл (будем называть ее работой цикла), равна разности (алгебраической сумме) работы расширения и работы сжатия. Понятно, что путь процесса сжатия следует выбрать таким образом, чтобы работа сжатия по абсолютной величине была меньше работы расширения, иначе работа цикла будет отрицательной, т.е. в результате цикла работа будет не производиться, а затрачиваться; впрочем, как будет показано в дальнейшем, в определенных случаях (циклы холодильных машин) используется именно такое построение цикла.
Циклические процессы, в результате которых производится работа, осуществляются в различных тепловых двигателях. Тепловым двигателем называют непрерывно действующую систему, осуществляющую круговые процессы (циклы), в которых теплота превращается в работу. Вещество, за счет изменения состояния которого получают работу в цикле, именуется рабочим телом.
Типовой процесс в pV координатах.
Работа цикла находит очень удобную графическую интерпретацию в p, V-диаграмме.
Если 1-а-2 — кривая процесса расширения, а 2-b-1 — кривая процесса сжатия, то площадь под кривой 1-а-2 равна работе расширения, площадь под кривой 2-b-1 — работе сжатия, а площадь, ограниченная замкнутой кривой (кривой цикла) 1-a-2-b-1, представляет собой работу цикла.
Работа цикла Lц равна количеству теплоты, подведенной извне к рабочему телу. В соответствии с первым законом термодинамики: работа, производимая двигателем, строго равна количеству теплоты, отобранной от внешнего источника и подведенной к рабочему телу двигателя. Если бы можно было построить такой тепловой двигатель, в котором количество производимой работы было больше, чем количество теплоты, подведенной к рабочему телу от внешнего источника, то это означало бы, что первый закон термодинамики (закон сохранения и превращения энергии) несправедлив. Из этого следовало бы, что можно построить такой тепловой двигатель, в котором работа производилась бы вообще без подвода теплоты извне, т.е. вечный двигатель.
Что касается теплоты Qц, которая превращается в работу, то следует отметить, что на одних участках цикла теплота к рабочему телу подводится, на других — отводится. Как будет показано далее, отвод определенного количества теплоты от рабочего тела на некоторых участках цикла является неотъемлемым условием осуществимости цикла любого теплового двигателя.
Если обозначить теплоту, подводимую к рабочему телу в цикле, через Q1, а теплоту, отводимую от рабочего тела в цикле, через Q2, то очевидно, что
И тогда в соответствии с первым законом термодинамики:
Введем новое понятие о так называемом термическом коэффициенте полезного действия (КПД) цикла. Термическим КПД цикла называют отношение работы цикла к количеству теплоты, подведенной к рабочему телу в цикле. Обозначая термический КПД цикла ηт, получаем в соответствии с этим определением:
Термический КПД цикла характеризует степень совершенства того или иного цикла: чем больше ηт, тем совершеннее цикл; при подводе к рабочему телу одного и того же количества теплоты Q1 в цикле, у которого ηт больше, производится большая ′ работа Lц.
Введем понятие об источниках теплоты. Систему, от которой отбирается теплота Q1, сообщаемая рабочему телу цикла, принято называть горячим источником теплоты , а систему, которой отдается теплота Q2, отбираемая от рабочего тела, холодным источником теплоты.
Спасибо за прочтение материала. В следующий раз материал про будет про обратимые и необратимые циклы, которые приведут нас к формулировке второго закона термодинамики.
Из первого закона термодинамики для кругового процесса следует:
= dU + , но т.к. в круговом процессе изменение внутренней энергии dU= 0, то = т.е. работа за цикл совершается получаемой извне теплоты: = , где – количество теплоты, полученной системой; – количество теплоты, отданное системой.
Термический КПД: = = = 1 .
Тепловые двигатели
Теплово́й дви́гатель — устройство, совершающее работу за счет использования внутренней энергии, тепловая машина, превращающая тепло в механическую энергию, использует зависимость теплового расширения вещества от температуры. (Возможно использование изменения не только объёма, но и формы рабочего тела, как это делается в твёрдотельных двигателях, где в качестве рабочего тела используется вещество в твёрдой фазе.) Действие теплового двигателя подчиняется законам термодинамики. Для работы необходимо создать разность давлений по обе стороны поршня двигателя или лопастей турбины. Для работы двигателя обязательно наличие топлива. Это возможно при нагревании рабочего тела (газа), который совершает работу за счёт изменения своей внутренней энергии. Повышение и понижение температуры осуществляется, соответственно, нагревателем и охладителем.
Тепловой двигатель – периодически действующий двигатель, совершающий работу за счёт полученной извне теплоты.
В тепловом двигателе используется прямой цикл.
Термостат – термодинамическая система, которая может обмениваться теплотой с телами без изменения собственной температуры.
Рабочее тело – термодинамическая система, совершающая круговой процесс и обменивающаяся энергией с другими телами. В тепловом двигателе рабочим телом обычно является газ.
Рассмотрим действие теплового двигателя (тепловой машины).
Под поршнем цилиндра (рис. 127) находится газ. Диаграмма состояния рабочего тела изображена в координатах (P,V) (рис. 128).
Рис. 127.
Приведём дно цилиндра в тепловой контакт с нагревателем, т.е. с телом, температура которого выше температуры газа в цилиндре. Газ будет нагреваться и расширяться по пути 1а2. Рабочее тело получит от нагревателя количество теплоты и совершит положительную работу А1.
Рис. 128.
По первому закону термодинамики: = (U2 – U1) + А1.
Теперь надо вернуть поршень в исходное положение, т.е. сжать газ. Это надо сделать так, чтобы работа А2, затраченная на сжатие, была меньше работы А1: А2 < А1. С этой целью приведём дно цилиндра в тепловой контакт с холодильником, т.е. телом, температура которого ниже температуры газа в цилиндре, и сожмём газ по пути 2б1. В результате рабочее тело вернётся в состояние 1 и отдаст холодильнику количество теплоты . По первому закону термодинамики: = (U2 – U1) – А2.
В итоге получаем: = А1 – А2 = А.
Таким образом, тепловая машина совершила круговой процесс, в результате которого нагреватель отдал тепло , а холодильник получил тепло ; тепло = пошло на производство работы А.
Вывод: для того, чтобы машина работала повторными циклами, часть полученной от нагревателя теплоты должна быть отдана холодильнику.
Схематическое устройство теплового двигателя
Схематическое устройство теплового двигателя изображено на рис. 129.
Рис. 129.
Принцип работы теплового двигателя
От термостата с температурой Т1 (нагреватель) за цикл отнимается количество теплоты , а термостату с температурой Т2 (холодильник; Т2 < Т1) за цикл передаётся количество теплоты , при этом совершается работа : А = .
Очевидно, чем полнее превращает тепловая машина полученную ею теплоту в работу, тем машина выгоднее. Эффективность тепловой машины характеризуется коэффициентом полезного действия (КПД):
= = = 1 1.
Из определения КПД следует, что он не может быть больше единицы.
Дадим сначала некоторые определения, которые позволят дать количественные формулировки второго начала термодинамики.
Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении через все промежуточные стадии; причем если система возвращается в исходное состояние, то в окружающих телах не происходит никаких изменений. Процесс, не удовлетворяющий этим условиям, является необратимым. Примеры необратимых процессов: диффузия, теплопередача, расширение газа в пустоту.
Обратимые процессы — это физическая абстракция. Тем не менее, многие процессы в природе и технике можно считать обратимыми. Существенно, что обратимые процессы являются наиболее экономичными и имеют максимальный коэффициент полезного действия.
Рис. 13.1
Циклом, или круговым процессом, называется процесс, при котором система возвращается в исходное состояние. График цикла представляет собой замкнутую кривую. Если цикл протекает по часовой стрелке, то такой цикл называется прямым (рис. 13.1).
Прямой цикл можно разбить на процессы расширения (а2) и сжатия (261) рабочего тела (газа), причем работа расширения (определяется площадью под кривой а2) положительна (dV>0), работа сжатия (определяется площадью под кривой 261) отрицательна (dV0). Таким образом, суммарная работа за цикл по модулю определяется площадью внутри замкнутой кривой. Если цикл протекает по часовой стрелке, то работа расширения больше работы сжатия, и очевидно, что суммарная работа за цикл положительна: А>0. Если цикл протекает против часовой стрелки (рис. 13.2), то он называется обратным. При этом работа расширения (определяется площадью
Рис. 13.2
под кривой 162) меньше работы сжатия, так что суммарная работа за цикл отрицательна: А0.
Прямой цикл применяется в тепловых машинах — они совершают циклическую работу за счет полученной извне теплоты. Обратный цикл применяется в холодильных машинах — в них за счет работы внешних сил теплота переносится от тела с низкой температурой (холодильника) к телу с более высокой температурой (нагревателю).
Коэффициентом полезного действия (КПД) тепловой машины называется отношение совершенной машиной работы А к количеству теплоты Q1, полученному рабочим телом от нагревателя
В результате кругового процесса система возвращается в исходное состояние, и, следовательно, изменение внутренней энергии газа за цикл равно нулю. Поэтому из первого начала термодинамики для кругового процесса (при dU = 0) следует, что работа за цикл равна полученному количеству теплоты
В общем случае тепловая машина не только получает теплоту Qu но и отдает теплоту Q2, так что суммарное количество теплоты, полученное системой, равно
В результате КПД кругового процесса равен
Чтобы КПД теплового двигателя достиг единицы, в соответствии с (13.4) необходимо, чтобы выполнялось условие Q2 = 0. Иными словами, тепловой двигатель должен иметь один источник теплоты, а это, как показал французский физик и инженер Карно (1796-1832), невозможно. Так, Карно доказал, что для работы теплового двигателя необходимо не менее двух источников теплоты с различными температурами.
Вопрос 33. Круговые процессы (циклы). КПД тепловой машины. Цикл Карно и его термический КПД.
Круговым процессом (циклом) называется такой процесс в результате совершения которого термодинамическое тело пройдя через ряд промежуточных состояний возвращалось в исходное. На диаграмме pV такие циклы изображаются виде замкнутой кривой. Работа газа за цикл численно равна площади цикла взятой со знаком плюс, если цикл прямой и со знаком минус, если цикл обратный. Тепловым двигателем называется установка в которой в результате многократного повторения круговых процессов осуществляется превращение внутренней энергии выделенной при сгорании топлива в механическую работу.
Первое начало термодинамики: |Q1| = U2 –U1 + |A1| , где Q1 – тепло, получаемое телом от нагревателя. 1 Н Т/Д: -|Q1|=U1 – U2 – |A2|, где Q2<0 – тепло переданное холодильником.
|Q1| – |Q2|=|A1| – |A2|. Из количества теплоты Q1 взаимная работа телом от нагревателя величина Q2 отдает холодильнику, а остальная часть идет на совершение работы. Для характеристики эффективности работы тепловой машины вводится физическая величина называемая КПД теплового двигателя – КПД – скалярная физич величина равная отношению полезной работы совершенное рабочим веществом за цикл к количеству теплоты полученного от нагревателя. . A=|Q1|-|Q2|. .
Предполагается, что все этапы круговых процессов обратимы, то есть не учитываются потери. Анализируя работу тепловых машин обладающих малым КПД французский ученый Карно предложил цикл так называемый идеальная тепловая машина, которая обладает максимальным КПД и состоит из чередующихся между собой двух изотермических и адиабатических процессов. При адиабатном расширении: 1)осуществляется понижение температуры; 2)совершается работа за счет внутренней энергии рабочего вещества.
1-2: Q1=A1; Q1=νRT1 ln V2/V1=A1; V2> V1, A1>0, Q1>0
2-3: δQ1=0, dU=vCvdT; ΔU23= vCv(T2-T1)<0
1 Н т/д: 0= dU+δA; A2=- ΔU23; A2= v Cv(T2-T1)>0
3-4: T=const; dU=0; 1 H т/д: A3=Q3; A3=vRT2 ln V4/V3<0; Q3<0
4-1: δQ=0; 1 H т/д: 0= dU+δA; 0= ΔU41 + A4; ΔU41= v Cv(T1-T2); A4= v Cv(T2-T1)<0;
A=A1+A2+A3+A4; A= vRT1 ln V2/V1+ vCv(T1-T2)+ vRT2 ln V4/V3+ v Cv(T2-T1);
A= vRT1 ln V2/V1+ vRT2 ln V4/V3; ;
– справедлива только для тепловых машин работающих на цикле Карно. Из этой формулы видно, что КПД не зависит от рода вещества использующийся в идеальной тепловой машине, а зависит только от температуры нагревателя и температуры холодильника.
Вопрос 34. Обратный цикл Карно. Холодильная машина.
Холодильной машиной называется установка которая в результате совершения работы внешними силами осуществляет передачу внутренней энергии от менее нагретого тела к более нагретому. Количество теплоты которое система получает от холодильника обозначается Q2/ Расширяясь система совершает работу А2. Рабочее вещество при этом переходит из состояния с внутренней энергией U1 в состояние U2. При более высоких температурах после приведения рабочего вещества в тепловой контакт с нагревателем получаем, что совершая работy A1’ рабочее вещество отдает Q1 нагревателю.
1 Н т/д: |Q2|=U2 – U1 + |A2|- при расширении рабочего тела
приведенного в контакт с холодильником.
1 Н т/д: -|Q1| = U1-U2-|A1|- при сжатии тела.
Рабочее тело за цикл совершает отрицательную работу
A=|A2|-|A1|. С другой стороны: A’=-A. A’=|Q1|-|Q2|
За один цикл работы холодильная машина более нагретому телу передает количество теплоты Q1 которое больше количества вещества Q2 взятого у менее нагретого тела на величину работы A’ совершенная внешними силами. Рабочим веществом служит пары легко кипящей жидкости.Роль внешних сил играет компрессор. Для характеристики эффекта холодильного цикла вводится величина равная отношению количества теплоты взятого от менее нагретого тела к работе внешних сил совершенных за цикл. . В отличие от КПД тепловой машины холодильный коэффициент может быть как больше так и меньше единицы. Тепло переданное от холодильника к нагревателю за счет совершения работы внешними силами над рабочим телом. Тогда, . Из формул вытекает особенность чем меньше Т2, тем меньше холодильный коэффициент. (Рисунок)
Вопрос 46. Образование вол в упругой среде. Продольные и поперечные волны. Уравнение плоской волны. Фазовая скорость. Принцип суперпозиции. Стоячие волны.
Если частицу упругой среды привести в колебательную систему то вследствии упругой связи она вовлечет в это колебательное движение соседнюю частицу. Эти соседние частицы в свою очередь воздействуют на соседние с ними и так далее. и колебания таким образом начнут распространяться в среде. Процесс распространения колебательного движения в среде называется волновым движением или волной. Волны делятся на: 1)продольные; 2)поперечные. Если каждая частица среды колебаний направлена перпендикулярно распространению волны – это поперечные волны. Если каждая частица среды колебаний распространяется в направлении волны то такая волна называется продольной. В поперечных волнах частица среды в направление распространения волны не перемещается. Колебания каждой последующей точки среды запаздывает по фазе относительно колебаний предыдущей точки. Гребни и впадины перемещаются вдоль направления волны. Скорость с которой в среде распространяются одинаковые фазы колебаний называется фазовой скоростью . Поверхности образованные точками с одинаковыми фазами называются поверхностями одинаковых фаз или волновыми поверхностями. Если поверхности одинаковых фаз представляют собой плоскости параллельные друг другу то это плоские волны. Уравнение плоской волны: – общее уравнение плоской бегущей волны, оно указывает смещение точки среды в момент времени t у которых координата х. – волновое число,тогда .Физический смысл волнового числа: Волновое число показывает сколько одинаковых волн укладывается на отрезке длиной 2пи метра. Если в среде распространяются одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются одна на другую, не возмущая друг друга. Это утверждение называется принципом суперпозицииволн. Принцип суперпозиции утверждает, что движение, вызванное распространением сразу нескольких волн, есть снова некоторый волновой процесс. Таким процессом, например, является звучание оркестра. Оно возникает от одновременного возбуждения звуковых колебаний воздуха отдельными музыкальными инструментами. Замечательно, что при наложении волн могут возникать особые явления. Их называют эффектами сложения или, как еще говорят, суперпозиции волн. Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.
Уравнение стоячей волны можно получить сложением уравнения падающей волны и уравнения отраженной волны .
Это уравнение стоячей волны определяет смещение любой точки волны.
Вопрос 33. Круговые процессы (циклы). КПД тепловой машины. Цикл Карно и его термический КПД.
Круговым процессом (циклом) называется такой процесс в результате совершения которого термодинамическое тело пройдя через ряд промежуточных состояний возвращалось в исходное. На диаграмме pV такие циклы изображаются виде замкнутой кривой. Работа газа за цикл численно равна площади цикла взятой со знаком плюс, если цикл прямой и со знаком минус, если цикл обратный. Тепловым двигателем называется установка в которой в результате многократного повторения круговых процессов осуществляется превращение внутренней энергии выделенной при сгорании топлива в механическую работу.
Первое начало термодинамики: |Q1| = U2 –U1 + |A1| , где Q1 – тепло, получаемое телом от нагревателя. 1 Н Т/Д: -|Q1|=U1 – U2 – |A2|, где Q2<0 – тепло переданное холодильником.
|Q1| – |Q2|=|A1| – |A2|. Из количества теплоты Q1 взаимная работа телом от нагревателя величина Q2 отдает холодильнику, а остальная часть идет на совершение работы. Для характеристики эффективности работы тепловой машины вводится физическая величина называемая КПД теплового двигателя – КПД – скалярная физич величина равная отношению полезной работы совершенное рабочим веществом за цикл к количеству теплоты полученного от нагревателя. . A=|Q1|-|Q2|. .
Предполагается, что все этапы круговых процессов обратимы, то есть не учитываются потери. Анализируя работу тепловых машин обладающих малым КПД французский ученый Карно предложил цикл так называемый идеальная тепловая машина, которая обладает максимальным КПД и состоит из чередующихся между собой двух изотермических и адиабатических процессов. При адиабатном расширении: 1)осуществляется понижение температуры; 2)совершается работа за счет внутренней энергии рабочего вещества.
1-2: Q1=A1; Q1=νRT1 ln V2/V1=A1; V2> V1, A1>0, Q1>0
2-3: δQ1=0, dU=vCvdT; ΔU23= vCv(T2-T1)<0
1 Н т/д: 0= dU+δA; A2=- ΔU23; A2= v Cv(T2-T1)>0
3-4: T=const; dU=0; 1 H т/д: A3=Q3; A3=vRT2 ln V4/V3<0; Q3<0
4-1: δQ=0; 1 H т/д: 0= dU+δA; 0= ΔU41 + A4; ΔU41= v Cv(T1-T2); A4= v Cv(T2-T1)<0;
A=A1+A2+A3+A4; A= vRT1 ln V2/V1+ vCv(T1-T2)+ vRT2 ln V4/V3+ v Cv(T2-T1);
A= vRT1 ln V2/V1+ vRT2 ln V4/V3; ;
– справедлива только для тепловых машин работающих на цикле Карно. Из этой формулы видно, что КПД не зависит от рода вещества использующийся в идеальной тепловой машине, а зависит только от температуры нагревателя и температуры холодильника.