Решение задач по коэффициент полезного действия

У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.
Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.
Задачи по физике на КПД теплового двигателя
Задача на вычисление КПД теплового двигателя №1
Условие
Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.
Решение
Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:
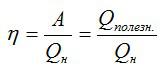
Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:
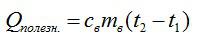
Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.
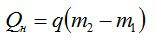
Подставляем значения и вычисляем:
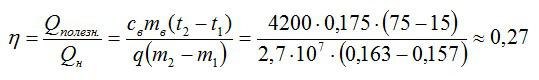
Ответ: 27%
Задача на вычисление КПД теплового двигателя №2
Условие
Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.
Решение
Найдем общее количество теплоты, которое произвел двигатель:
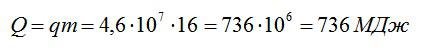
Теперь можно рассчитать КПД:
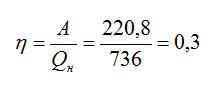
Или, умножая на 100, получаем значение КПД в процентах:
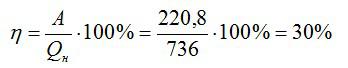
Ответ: 30%.
Задача на вычисление КПД теплового двигателя №3
Условие
Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.
Решение
КПД идеальной тепловой машины:
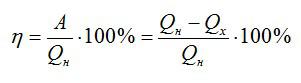
По условию:
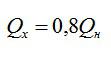
Вычислим сначала работу, а затем КПД:
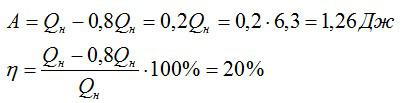
Ответ: 20%; 1,26 Дж.
Задача на вычисление КПД теплового двигателя №4
Условие
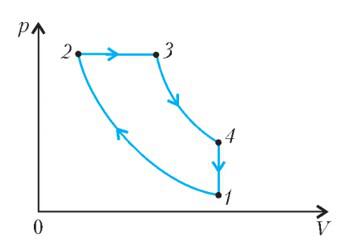
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.
Решение
Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.
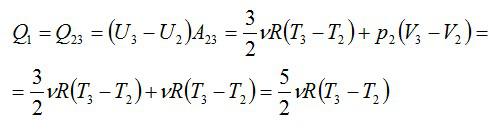
Аналогично:
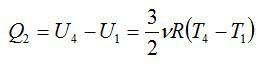
Получим результат:
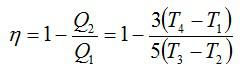
Ответ: См. выше.
Задача на вычисление КПД теплового двигателя №5
Условие
Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.
Решение
Запишем формулу для КПД:
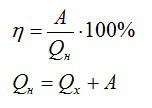
Отсюда:
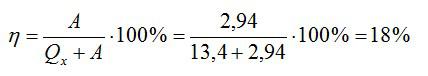
Ответ: 18%
Вопросы на тему тепловые двигатели
Вопрос 1. Что такое тепловой двигатель?
Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.
Вопрос 2. Приведите примеры тепловых двигателей.
Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:
- ракетный двигатель;
- авиационный двигатель;
- газовая турбина.
Вопрос 3. Может ли КПД двигателя быть равен единице?
Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.
КПД реальных двигателей редко превышает 30%.
Вопрос 4. Что такое КПД?
Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.
Вопрос 5. Что такое удельная теплота сгорания топлива?
Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.
Задачи и вопросы на цикл Карно
Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.
Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).
Задача на цикл Карно №1
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.
Решение
Рассчитаем КПД цикла:
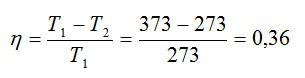
С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:
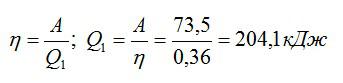
Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:
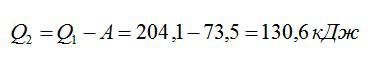
Ответ: 0,36; 204,1 кДж; 130,6 кДж.
Задача на цикл Карно №2
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.
Решение
Формула для КПД цикла Карно:
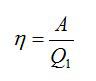
Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:
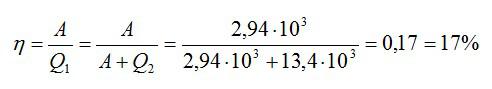
Ответ: 17%.
Задача на цикл Карно №3
Условие
Изобразите цикл Карно на диаграмме и опишите его
Решение
Цикл Карно на диаграмме PV выглядит следующим образом:

- 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
- 2-3. Адиабатическое расширение, тепло не подводится;
- 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
- 4-1. Адиабатическое сжатие.
Ответ: см. выше.
Вопрос на цикл Карно №1
Сформулируйте первую теорему Карно
Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.
Вопрос на цикл Карно №2
Может ли коэффициент полезного действия в цикле Карно быть равным 100%?
Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.
Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.
Источник
Задачи по теме Кпд механизмов |
Рады приветствовать учеников всех учебных заведений всех возрастов на нашем сайте!
Здесь вы найдете решебники и решения задач бесплатно, без регистрации.
davay5.com
Источник
§ 1 Повторение формул по теме урока
В этом уроке мы рассмотрим решение задач на расчет механической работы и мощности, коэффициент полезного действия простых механизмов.
Для решения задач нужно знать формулы:
· Механическая работа равна произведению модуля силы на пройденный путь: A = F · s. Мощность равна отношению работы ко времени ее выполнения: N = A / t.
· Потенциальная энергия тела, поднятого над землей, вычисляется по формуле:
Еп = mgh.
· Кинетическая энергия – это энергия движения тела, зависит от скорости движения и массы тела: Ек = m υ2/2.
· Коэффициент полезного действия равен отношению полезной работы ко всей полной совершенной работе: η = Апоез/ Аполн.
· Простые механизмы, используемые для выполнения работы, позволяют получить выигрыш в силе, например, подвижный блок дает выигрыш в силе в 2 раза: Pгруза = 2 · Fприл, но при этом проигрываем в пути также в 2 раза.
§ 2 Решение задач
С помощью рычага груз массой 100 кг был поднят равномерно на высоту 80 см. При этом длинное плечо рычага, к которому приложена сила 600 Н, опустилось на 2 м. Определите коэффициент полезного действия рычага.
Запишем условие задачи: масса груза m = 100 кг, сила F = 600 Н, путь, пройденный грузом s1 = h = 80 см = 0,8 м, путь, пройденный длинным плечом рычага s2 = 2 м. Найти кпд η.
Решение: Чтобы найти кпд, определим полезную и полную работу. Полезная работа – это работа по поднятию груза весом mgна 80 см: Аполез = P · s1 = mgh = 100 кг · 10Н/кг · 0,8 м = 800 Дж. Полная работа – это работа, совершенная силой, приложенной к длинному плечу рычага, Аполн = F · s2 = 600 Н · 2 м = 1200 Дж.
Тогда кпд механизма равен: η = Аполез/ Аполн = 800 Дж / 1200 Дж = 0, 67 = 67%

Какая сила потребуется для равномерного поднятия груза массой 200 кг по наклонной плоскости, имеющей кпд 60%? Высота наклонной плоскости –1,5 м, длина – 10 м.
Запишем условие задачи: масса m = 200 кг, высота наклонной плоскости h= 1,5 м, длина l = 10 м, кпд установки η = 60% = 0,6 в системе СИ. Найти приложенную силу F.
Решение: При помощи наклонной плоскости поднимают груз, то есть совершают работу. Полезная работа равна произведению веса груза mg на высоту h. Полная работа совершается приложенной силой на пути, равном длине наклонной плоскости: Аполн = F · s2 = F · l.
Подставим записанные формулы в формулу коэффициента полезного действия и выразим неизвестную величину – приложенную силу: F равно mgh делим на кпд и l. Вычислим, подставив числовые значения известных величин. Ответ: для подъема груза требуется сила 500 Н.

Водяной насос подает 300 л воды в минуту на высоту 20 м. Определить мощность двигателя насоса, если его кпд равен 80%.
Запишем условие задачи: объем воды V = 300 л = 0,3 м3, время работы t = 1 мин = 60 с, путь, пройденный водой, равен высоте s1 = h = 20 м, плотность воды ρ = 1000 кг/м3, кпд насоса η = 80% = 0,8. Найти мощность двигателя N.
Решение: При помощи насоса совершают работу по поднятию воды. Полезная работа равна произведению веса воды на высоту: Аполез = P · s1 = mgh, массу воды найдем по формуле плотности m = ρ · V = 1000 кг/м3 · 0,3 м3 = 300 кг. Тогда полезная работа составит 60 000 Дж.
Полную работу, совершенную двигателем насоса, можно найти по формуле мощности: Аполн = N · t. Подставим в формулу кпд формулу полной работы и выразим неизвестную мощность: N= Аполез/ кпд и время. Вычислим. Ответ: мощность двигателя насоса 1250 Вт.

Итак, при решении задач на расчет коэффициента полезного действия нужно правильно определить, что является полезной работой и что является полной работой. Для этого можно поставить вопрос: с какой целью применяют тот или иной механизм? Ответ на него позволяет определить полезную работу. Полной работой является работа, совершенная самим механизмом.
§ 3 Важно запоминить
Коэффициент полезного действия – это величина, показывающая долю полезной работы от всей полной совершенной работы. КПД выражают в процентах. При решении задач на расчет коэффициента полезного действия нужно определить полезную работу и полную совершенную работу. КПД механизмов всегда меньше 100%.
Источник
Подробности
Просмотров: 659
«Физика – 10 класс»
Для решения задач надо воспользоваться известными выражениями для определения КПД тепловых машин и иметь в виду, что выражение (13.17) справедливо только для идеальной тепловой машины.
Задача 1.
В котле паровой машины температура 160 °С, а температура холодильника 10 °С.
Какую максимальную работу может теоретически совершить машина, если в топке, коэффициент полезного действия которой 60 %, сожжён уголь массой 200 кг с удельной теплотой сгорания 2,9 • 107 Дж/кг?
Р е ш е н и е.
Максимальную работу может совершить идеальная тепловая машина, работающая по циклу Карно, КПД которой η = (Т1 – Т2)/Т1, где Т1 и Т2 — абсолютные температуры нагревателя и холодильника. Для любой тепловой машины КПД определяется по формуле η = A/Q1, где А — работа, совершаемая тепловой машиной, Q1 — количество теплоты, полученной машиной от нагревателя.
Из условия задачи ясно, что Q1 — это часть количества теплоты, выделившейся при сгорании топлива: Q1 = η1mq.
Тогда  откуда А = η1mq(1 – Т2/Т1) = 1,2 • 109 Дж.
откуда А = η1mq(1 – Т2/Т1) = 1,2 • 109 Дж.
Задача 2.
Паровая машина мощностью N = 14,7 кВт потребляет за 1 ч работы топливо массой m = 8,1 кг, с удельной теплотой сгорания q = 3,3 • 107 Дж/кг.
Температура котла 200 °С, холодильника 58 °С.
Определите КПД этой машины и сравните его с КПД идеальной тепловой машины.
Р е ш е н и е.
КПД тепловой машины равен отношению совершённой механической работы А к затраченному количеству теплоты Qlt выделяющейся при сгорании топлива.
Количество теплоты Q1 = mq.
Совершённая за это же время работа А = Nt.
Таким образом, η = A/Q1 = Nt/qm = 0,198, или η ≈ 20%.
Для идеальной тепловой машины  η < ηид.
η < ηид.
Задача 3.
Идеальная тепловая машина с КПД η работает по обратному циклу (рис. 13.15).

Какое максимальное количество теплоты можно забрать от холодильника, совершив механическую работу А?
Р е ш е н и е.
Поскольку холодильная машина работает по обратному циклу, то для перехода тепла от менее нагретого тела к более нагретому необходимо, чтобы внешние силы совершили положительную работу.
Принципиальная схема холодильной машины: от холодильника отбирается количество теплоты Q2, внешними силами совершается работа и нагревателю передаётся количество теплоты Q1.
Следовательно,  Q2 = Q1(1 – η), Q1 = A/η.
Q2 = Q1(1 – η), Q1 = A/η.
Окончательно Q2 = (A/η)(1 – η).
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Основы термодинамики. Тепловые явления – Физика, учебник для 10 класса – Класс!ная физика
Насыщенный пар —
Давление насыщенного пара —
Влажность воздуха —
Примеры решения задач по теме «Насыщенный пар. Влажность воздуха» —
Кристаллические тела —
Аморфные тела —
Внутренняя энергия —
Работа в термодинамике —
Примеры решения задач по теме «Внутренняя энергия. Работа» —
Количество теплоты. Уравнение теплового баланса —
Примеры решения задач по теме: «Количество теплоты. Уравнение теплового баланса» —
Первый закон термодинамики —
Применение первого закона термодинамики к различным процессам —
Примеры решения задач по теме: «Первый закон термодинамики» —
Второй закон термодинамики —
Статистический характер второго закона термодинамики —
Принцип действия тепловых двигателей. Коэффициент полезного действия (КПД) тепловых двигателей —
Примеры решения задач по теме: «КПД тепловых двигателей»
Источник
1. Повторение формул и величин
Данный урок посвящён решению задач. Мы рассмотрим несколько задач на нахождение КПД тепловых установок. Кроме непосредственно КПД, в них фигурируют формулы для количества теплоты, необходимого для нагревания вещества или выделяемого при охлаждении, а также количества теплоты, которое выделяется при сгорании топлива.
Все эти вопросы мы уже рассматривали на прошлых уроках. Однако мы ещё не уделяли отдельное внимание задачам, в которых теплота сгорания топлива идёт на нагревание тел.
Поэтому на этом уроке мы подробно рассмотрим решение задач на нахождение КПД тепловых установок и двигателей. Как мы знаем, любая тепловая установка характеризуется своим КПД. Для нахождения КПД нам могут пригодиться следующие формулы:
![]() – количество теплоты, которое выделяется при сгорании топлива (
– количество теплоты, которое выделяется при сгорании топлива (![]() – удельная теплота сгорания,
– удельная теплота сгорания, ![]() – масса топлива);
– масса топлива);
![]() – количество теплоты, которое выделяется при охлаждении или необходимо для нагревания вещества (
– количество теплоты, которое выделяется при охлаждении или необходимо для нагревания вещества (![]() – удельная теплоёмкость вещества,
– удельная теплоёмкость вещества, ![]() – масса вещества,
– масса вещества, ![]() – конечная температура вещества,
– конечная температура вещества, 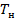 – начальная температура вещества);
– начальная температура вещества);
![]() – КПД установки (
– КПД установки (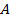 – работа, совершённая рабочим телом,
– работа, совершённая рабочим телом, ![]() – количество теплоты, полученное от нагревателя);
– количество теплоты, полученное от нагревателя);
Большинство из величин, встречающихся в формулах, либо даны в условии, либо являются искомыми. Однако удельная теплоёмкость вещества и удельная теплота сгорания берутся из соответствующих таблиц. Напомним единицы измерения этих величин: ![]() .
.
Кроме этих величин в задачах могут встречаться ещё две табличные величины: ![]() – удельная теплота парообразования,
– удельная теплота парообразования, ![]() – удельная теплота плавления. Однако на этом уроке они нам не понадобятся, поэтому подробно останавливаться на них не будем.
– удельная теплота плавления. Однако на этом уроке они нам не понадобятся, поэтому подробно останавливаться на них не будем.
Для удобства составим таблицу с теми значениями табличных величин, которые понадобятся на этом уроке при решении задач.
cellspacing=”0″>
Вещество | Удельная теплоёмкость | Удельная теплота сгорания |
Вода |
| – |
Спирт |
|
|
Бензин |
|
|
2. Задача №1 на нахождение КПД
На спиртовке нагревают воду. Взяли ![]() воды и нагрели от
воды и нагрели от ![]() до
до ![]() . При этом масса спиртовки уменьшилась с
. При этом масса спиртовки уменьшилась с ![]() до
до ![]() . Найти КПД тепловой установки.
. Найти КПД тепловой установки.
Решение
Запишем краткое условие задачи.
cellspacing=”0″>
Дано: | СИ | Решение: Вначале выпишем формулу для КПД:
В данном случае мы заменили работу полезным количеством теплоты, то есть тем количеством теплоты, которое пошло непосредственно на нагрев воды. |
|
| |
Найти:
|
Прежде чем решать задачу, необходимо определиться с процессами, которые происходят в данной задаче. Первый процесс – это сгорание топлива. Второй – нагревание воды.
Полезное количество теплоты, то есть то тепло, которое пошло непосредственно на нагревание воды, можно вычислить по формуле:
![]()
Количество теплоты, выделенное нагревателем, то есть, в данном случае, тепло, выделившееся при сгорании спирта:
![]()
Массу сгоревшего спирта найти легко: это та масса, на которую уменьшилась масса спиртовки, то есть: ![]() .
.
Получаем: ![]() .
.
Осталось вычислить КПД установки:
![]() .
.
Заметим, что КПД может вычисляться не только в процентах, но и в долях. К примеру, для данной задачи ответ может быть: ![]() .
.
Если анализировать данную задачу, то можно увидеть, что только четвёртая часть (приблизительно) тепла, которое выделяется при сгорании спирта, идёт на нагревание воды. С одной стороны, это кажется достаточно малым значением, но, с другой стороны, для многих тепловых машин такое значение КПД оказывается даже большим.
Ответ:![]() .
.
3. Задача №2 на нахождение КПД
Тепловой двигатель совершил полезную работу ![]() и израсходовал при этом
и израсходовал при этом ![]() бензина. Найти КПД теплового двигателя.
бензина. Найти КПД теплового двигателя.
Решение
Запишем краткое условие задачи.
cellspacing=”0″>
Дано: | СИ | Решение: Вначале выпишем формулу для КПД: |
|
| |
Найти:
|
Как и в прошлой задаче, воспользуемся следующей формулой: ![]() .
.
Находим КПД:
![]() .
.
Ответ:![]() .
.
Итак, мы решили несколько задач на нахождение КПД тепловых двигателей и установок, вспомнили основные формулы и величины, которые требуются для решения таких задач.
На следующем уроке мы рассмотрим более сложные задачи, которые могут встретиться в теме «Тепловые явления».
Вопросы к конспектам
Каков КПД теплового двигателя, который совершил полезную работу ![]() , если при полном сгорании топлива выделилась бы энергия
, если при полном сгорании топлива выделилась бы энергия ![]() ?
?
Израсходовав ![]() бензина, тепловой двигатель совершил полезную работу
бензина, тепловой двигатель совершил полезную работу ![]() . Каков КПД этого двигателя?
. Каков КПД этого двигателя?
Сколько природного газа необходимо сжечь для совершения полезной работы ![]() , если КПД двигателя
, если КПД двигателя ![]() ?
?
Источник
