Примеры полезного резонанса в электрических цепях

 êîëåáàòåëüíîì êîíòóðå, îáëàäàþùåì èíäóêòèâíîñòüþ L, åìêîñòüþ C è ñîïðîòèâëåíèåì R, ñâîáîäíûå ýëåêòðè÷åñêèå êîëåáàíèÿ èìåþò òåíäåíöèþ ê çàòóõàíèþ. ×òîáû êîëåáàíèÿ íå çàòóõàëè, íåîáõîäèìî ïåðèîäè÷åñêè ïîïîëíÿòü êîíòóð ýíåðãèåé, òîãäà âîçíèêíóò âûíóæäåííûå êîëåáàíèÿ, êîòîðûå íå áóäóò çàòóõàòü, âåäü âíåøíÿÿ ïåðåìåííàÿ ÝÄÑ ñòàíåò òåïåðü ïîääåðæèâàòü êîëåáàíèÿ â êîíòóðå.
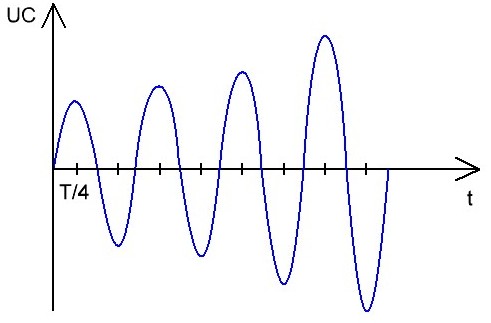
Åñëè êîëåáàíèÿ ïîääåðæèâàòü èñòî÷íèêîì âíåøíåé ãàðìîíè÷åñêîé ÝÄÑ, ÷àñòîòà êîòîðîé f î÷åíü áëèçêà ê ðåçîíàíñíîé ÷àñòîòå êîëåáàòåëüíîãî êîíòóðà F, òî àìïëèòóäà ýëåêòðè÷åñêèõ êîëåáàíèé U â êîíòóðå ñòàíåò ðåçêî âîçðàñòàòü, òî åñòü íàñòóïèò ÿâëåíèå ýëåêòðè÷åñêîãî ðåçîíàíñà.
Åìêîñòü â öåïè ïåðåìåííîãî òîêà
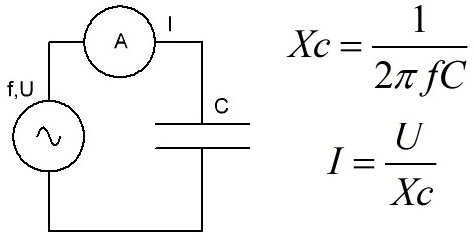
Ðàññìîòðèì ñíà÷àëà ïîâåäåíèå êîíäåíñàòîðà C â öåïè ïåðåìåííîãî òîêà. Åñëè ê ãåíåðàòîðó, íàïðÿæåíèå U íà âûâîäàõ êîòîðîãî ìåíÿåòñÿ ïî ãàðìîíè÷åñêîìó çàêîíó, ïðèñîåäèíèòü êîíäåíñàòîð C, òî çàðÿä q íà îáêëàäêàõ êîíäåíñàòîðà ñòàíåò ìåíÿòüñÿ òàêæå ïî ãàðìîíè÷åñêîìó çàêîíó, êàê è òîê I â öåïè. ×åì áîëüøå åìêîñòü êîíäåíñàòîðà, è ÷åì âûøå ÷àñòîòà f, ïðèêëàäûâàåìîé ê íåìó ãàðìîíè÷åñêîé ÝÄÑ, òåì áîëüøå îêàæåòñÿ òîê I.
Ñ ýòèì ôàêòîì ñâÿçàíî ïðåäñòàâëåíèå î òàê íàçûâàåìîì åìêîñòíîì ñîïðîòèâëåíèè êîíäåíñàòîðà XC, êîòîðîå îí âíîñèò â öåïü ïåðåìåííîãî òîêà, îãðàíè÷èâàÿ òîê ïîäîáíî àêòèâíîìó ñîïðîòèâëåíèþ R, íî â ñðàâíåíèè ñ àêòèâíûì ñîïðîòèâëåíèåì, êîíäåíñàòîð íå ðàññåèâàåò ýíåðãèþ â âèäå òåïëà.
Åñëè àêòèâíîå ñîïðîòèâëåíèå ðàññåèâàåò ýíåðãèþ, è òàêèì îáðàçîì îãðàíè÷èâàåò òîê, òî êîíäåíñàòîð îãðàíè÷èâàåò òîê ïðîñòî èç-çà òîãî, ÷òî â íåì íå óñïåâàåò óìåñòèòüñÿ áîëüøå çàðÿäà, ÷åì ãåíåðàòîð ìîæåò äàòü çà ÷åòâåðòü ïåðèîäà, ê òîìó æå â ñëåäóþùóþ ÷åòâåðòü ïåðèîäà êîíäåíñàòîð îòäàåò ýíåðãèþ, êîòîðàÿ íàêîïèëàñü â ýëåêòðè÷åñêîì ïîëå åãî äèýëåêòðèêà, îáðàòíî ãåíåðàòîðó, òî åñòü õîòü òîê è îãðàíè÷åí, ýíåðãèÿ íå ðàññåèâàåòñÿ (ïîòåðÿìè â ïðîâîäàõ è â äèýëåêòðèêå ïðåíåáðåæåì).
Èíäóêòèâíîñòü â öåïè ïåðåìåííîãî òîêà
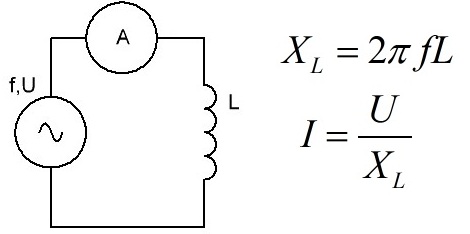
Òåïåðü ðàññìîòðèì ïîâåäåíèå èíäóêòèâíîñòè L â öåïè ïåðåìåííîãî òîêà. Åñëè âìåñòî êîíäåíñàòîðà ïðèñîåäèíèòü ê ãåíåðàòîðó êàòóøêó, îáëàäàþùóþ èíäóêòèâíîñòüþ L, òî ïðè ïîäà÷å îò ãåíåðàòîðà ñèíóñîèäàëüíîé (ãàðìîíè÷åñêîé) ÝÄÑ íà âûâîäû êàòóøêè, – â íåé íà÷íåò âîçíèêàòü ÝÄÑ ñàìîèíäóêöèè, ïîñêîëüêó ïðè èçìåíåíèè òîêà ÷åðåç èíäóêòèâíîñòü, óâåëè÷èâàþùååñÿ ìàãíèòíîå ïîëå êàòóøêè ñòðåìèòñÿ ïðåïÿòñòâîâàòü ðîñòó òîêà (çàêîí Ëåíöà), òî åñòü ïîëó÷àåòñÿ, ÷òî êàòóøêà âíîñèò â öåïü ïåðåìåííîãî òîêà èíäóêòèâíîå ñîïðîòèâëåíèå XL – äîïîëíèòåëüíîå ê ñîïðîòèâëåíèþ ïðîâîäà R.
×åì áîëüøå èíäóêòèâíîñòü äàííîé êàòóøêè, è ÷åì âûøå ÷àñòîòà F òîêà ãåíåðàòîðà, òåì âûøå èíäóêòèâíîå ñîïðîòèâëåíèå XL è ìåíüøå òîê I, âåäü òîê ïðîñòî íå óñïåâàåò óñòàíàâëèâàòüñÿ, ïîòîìó ÷òî ÝÄÑ ñàìîèíäóêöèè êàòóøêè åìó ìåøàåò. È êàæäûå ÷åòâåðòü ïåðèîäà ýíåðãèÿ, íàêîïëåííàÿ â ìàãíèòíîì ïîëå êàòóøêè, âîçâðàùàåòñÿ ê ãåíåðàòîðó (ïîòåðÿìè â ïðîâîäàõ ïîêà ïðåíåáðåæåì).
Ïîëíîå ñîïðîòèâëåíèå ñ ó÷åòîì R
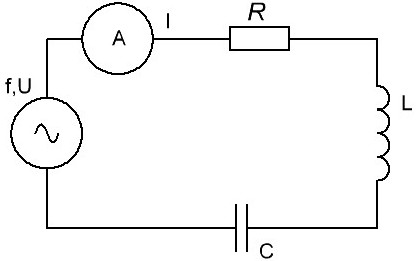
 ëþáîì ðåàëüíîì êîëåáàòåëüíîì êîíòóðå ïîñëåäîâàòåëüíî ñîåäèíåíû èíäóêòèâíîñòü L, åìêîñòü C è àêòèâíîå ñîïðîòèâëåíèå R.
Èíäóêòèâíîñòü è åìêîñòü äåéñòâóþò íà òîê ïðîòèâîïîëîæíî â êàæäóþ ÷åòâåðòü ïåðèîäà ãàðìîíè÷åñêîé ÝÄÑ èñòî÷íèêà: íà îáêëàäêàõ êîíäåíñàòîðà â ïðîöåññå çàðÿäà íàïðÿæåíèå óâåëè÷èâàåòñÿ, õîòÿ óìåíüøàåòñÿ òîê, à ïðè íàðàñòàíèè òîêà ÷åðåç èíäóêòèâíîñòü òîê õîòü è èñïûòûâàåò èíäóêòèâíîå ñîïðîòèâëåíèå, íî íàðàñòàåò è ïîääåðæèâàåòñÿ.
È âî âðåìÿ ðàçðÿäà: ðàçðÿäíûé òîê êîíäåíñàòîðà ñíà÷àëà áîëüøîé, íàïðÿæåíèå íà åãî îáêëàäêàõ ñòðåìèòñÿ óñòàíîâèòü áîëüøîé òîê, à èíäóêòèâíîñòü ïðåïÿòñòâóåò óâåëè÷åíèþ òîêà, è ÷åì áîëüøå èíäóêòèâíîñòü, òåì ìåíüøèé ðàçðÿäíûé òîê áóäåò èìåòü ìåñòî. Ïðè ýòîì àêòèâíîå ñîïðîòèâëåíèå R âíîñèò ÷èñòî àêòèâíûå ïîòåðè. Òî åñòü ïîëíîå ñîïðîòèâëåíèå Z, ïîñëåäîâàòåëüíî âêëþ÷åííûõ L, C è R, ïðè ÷àñòîòå èñòî÷íèêà f, áóäåò ðàâíî:
Çàêîí Îìà äëÿ ïåðåìåííîãî òîêà
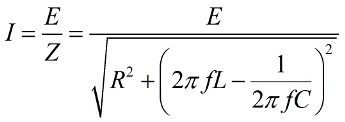
Èç çàêîíà Îìà äëÿ ïåðåìåííîãî òîêà î÷åâèäíî, ÷òî àìïëèòóäà âûíóæäåííûõ êîëåáàíèé ïðîïîðöèîíàëüíà àìïëèòóäå ÝÄÑ è çàâèñèò îò ÷àñòîòû. Ïîëíîå ñîïðîòèâëåíèå öåïè áóäåò íàèìåíüøèì, à àìïëèòóäà òîêà áóäåò íàèáîëüøåé ïðè óñëîâèè, ÷òî èíäóêòèâíîå ñîïðîòèâëåíèå è åìêîñòíîå ïðè äàííîé ÷àñòîòå ðàâíû ìåæäó ñîáîé, â ýòîì ñëó÷àå íàñòóïèò ðåçîíàíñ. Îòñþäà æå âûâîäèòñÿ ôîðìóëà äëÿ ðåçîíàíñíîé ÷àñòîòû êîëåáàòåëüíîãî êîíòóðà:
Ðåçîíàíñ íàïðÿæåíèé
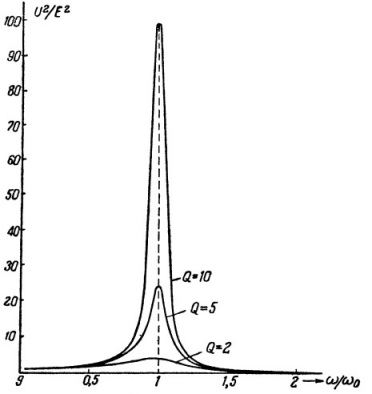
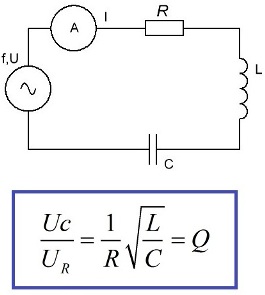
Êîãäà èñòî÷íèê ÝÄÑ, åìêîñòü, èíäóêòèâíîñòü è ñîïðîòèâëåíèå âêëþ÷åíû ìåæäó ñîáîé ïîñëåäîâàòåëüíî, òî ðåçîíàíñ â òàêîé öåïè íàçûâàåòñÿ ïîñëåäîâàòåëüíûì ðåçîíàíñîì èëè ðåçîíàíñîì íàïðÿæåíèé. Õàðàêòåðíàÿ ÷åðòà ðåçîíàíñà íàïðÿæåíèé çíà÷èòåëüíûå íàïðÿæåíèÿ íà åìêîñòè è íà èíäóêòèâíîñòè, ïî ñðàâíåíèþ ñ ÝÄÑ èñòî÷íèêà.
Ïðè÷èíà ïîÿâëåíèÿ òàêîé êàðòèíû î÷åâèäíà. Íà àêòèâíîì ñîïðîòèâëåíèè ïî çàêîíó Îìà áóäåò íàïðÿæåíèå Ur, íà åìêîñòè Uc, íà èíäóêòèâíîñòè Ul, è ñîñòàâèâ îòíîøåíèå Uc ê Ur ìîæíî íàéòè âåëè÷èíó äîáðîòíîñòè Q. Íàïðÿæåíèå íà åìêîñòè áóäåò â Q ðàç áîëüøå ÝÄÑ èñòî÷íèêà, òàêîå æå íàïðÿæåíèå îêàæåòñÿ ïðèëîæåííûì ê èíäóêòèâíîñòè.
Òî åñòü ðåçîíàíñ íàïðÿæåíèé ïðèâîäèò ê âîçðàñòàíèþ íàïðÿæåíèÿ íà ðåàêòèâíûõ ýëåìåíòàõ â Q ðàç, à ðåçîíàíñíûé òîê áóäåò îãðàíè÷åí ÝÄÑ èñòî÷íèêà, åãî âíóòðåííèì ñîïðîòèâëåíèåì è àêòèâíûì ñîïðîòèâëåíèåì öåïè R. Òàêèì îáðàçîì, ñîïðîòèâëåíèå ïîñëåäîâàòåëüíîãî êîíòóðà íà ðåçîíàíñíîé ÷àñòîòå ìèíèìàëüíî.
Ïðèìåíåíèå ðåçîíàíñà íàïðÿæåíèé
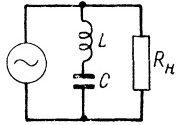
ßâëåíèå ðåçîíàíñà íàïðÿæåíèé èñïîëüçóþò â ýëåêòðè÷åñêèõ ôèëüòðàõ ðàçíîãî ðîäà, íàïðèìåð åñëè íåîáõîäèìî óñòðàíèòü èç ïåðåäàâàåìîãî ñèãíàëà ñîñòàâëÿþùóþ òîêà îïðåäåëåííîé ÷àñòîòû, òî ïàðàëëåëüíî ïðèåìíèêó ñòàâÿò öåïî÷êó èç ñîåäèíåííûõ ïîñëåäîâàòåëüíî êîíäåíñàòîðà è êàòóøêè èíäóêòèâíîñòè, ÷òîáû òîê ðåçîíàíñíîé ÷àñòîòû ýòîé LC-öåïî÷êè çàìêíóëñÿ áû ÷åðåç íåå, è íå ïîïàë ê áû ïðèåìíèêó.
Òîãäà òîêè ÷àñòîòû äàëåêîé îò ðåçîíàíñíîé ÷àñòîòû LC-öåïî÷êè áóäóò ïðîõîäèòü â íàãðóçêó áåñïðåïÿòñòâåííî, è òîëüêî áëèçêèå ê ðåçîíàíñó ïî ÷àñòîòå òîêè – áóäóò íàõîäèòü ñåáå êðîò÷àéøèé ïóòü ÷åðåç LC-öåïî÷êó.
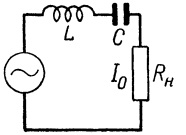
Èëè íàîáîðîò. Åñëè íåîáõîäèìî ïðîïóñòèòü òîëüêî òîê îïðåäåëåííîé ÷àñòîòû, òî LC-öåïî÷êó âêëþ÷àþò ïîñëåäîâàòåëüíî ïðèåìíèêó, òîãäà ñîñòàâëÿþùèå ñèãíàëà íà ðåçîíàíñíîé ÷àñòîòå öåïî÷êè ïðîéäóò ê íàãðóçêå ïî÷òè áåç ïîòåðü, à ÷àñòîòû äàëåêèå îò ðåçîíàíñà îêàæóòñÿ ñèëüíî îñëàáëåíû è ìîæíî ñêàçàòü, ÷òî ê íàãðóçêå ñîâñåì íå ïîïàäóò. Äàííûé ïðèíöèï ïðèìåíèì ê ðàäèîïðèåìíèêàì, ãäå ïåðåñòðàèâàåìûé êîëåáàòåëüíûé êîíòóð íàñòðàèâàþò íà ïðèåì ñòðîãî îïðåäåëåííîé ÷àñòîòû íóæíîé ðàäèîñòàíöèè.
Âîîáùå ðåçîíàíñ íàïðÿæåíèé â ýëåêòðîòåõíèêå ÿâëÿåòñÿ íåæåëàòåëüíûì ÿâëåíèåì, ïîñêîëüêó îí âûçûâàåò ïåðåíàïðÿæåíèÿ è âûõîä èç ñòðîÿ îáîðóäîâàíèÿ.
 êà÷åñòâå ïðîñòîãî ïðèìåðà ìîæíî ïðèâåñòè äëèííóþ êàáåëüíóþ ëèíèþ, êîòîðàÿ ïî êàêîé-òî ïðè÷èíå îêàçàëàñü íå ïîäêëþ÷åííîé ê íàãðóçêå, íî ïðè ýòîì ïèòàåòñÿ îò ïðîìåæóòî÷íîãî òðàíñôîðìàòîðà. Òàêàÿ ëèíèÿ ñ ðàñïðåäåëåííîé åìêîñòüþ è èíäóêòèâíîñòüþ, åñëè åå ðåçîíàíñíàÿ ÷àñòîòà ñîâïàäåò ñ ÷àñòîòîé ïèòàþùåé ñåòè, ïðîñòî áóäåò ïðîáèòà è âûéäåò èç ñòðîÿ. ×òîáû ïðåäîòâðàòèòü ðàçðóøåíèå êàáåëåé îò ñëó÷àéíîãî ðåçîíàíñà íàïðÿæåíèé, ïðèìåíÿþò âñïîìîãàòåëüíóþ íàãðóçêó.
Íî èíîãäà ðåçîíàíñ íàïðÿæåíèé èãðàåò íàì íà ðóêó è íå òîëüêî â ðàäèîïðèåìíèêàõ. Íàïðèìåð, áûâàåò, ÷òî â ñåëüñêîé ìåñòíîñòè íàïðÿæåíèå â ñåòè íåïðåäñêàçóåìî óïàëî, à ñòàíêó íóæíî íàïðÿæåíèå íå ìåíåå 220 âîëüò.  ýòîì ñëó÷àå ÿâëåíèå ðåçîíàíñà íàïðÿæåíèé ñïàñàåò.
Äîñòàòî÷íî ïîñëåäîâàòåëüíî ñî ñòàíêîì (åñëè ïðèâîäîì â íåì ÿâëÿåòñÿ àñèíõðîííûé äâèãàòåëü) âêëþ÷èòü ïî íåñêîëüêî êîíäåíñàòîðîâ íà ôàçó, è òàêèì îáðàçîì íàïðÿæåíèå íà îáìîòêàõ ñòàòîðà ïîäíèìåòñÿ.
Çäåñü âàæíî ïðàâèëüíî ïîäîáðàòü êîëè÷åñòâî êîíäåíñàòîðîâ, ÷òîáû îíè òî÷íî ñêîìïåíñèðîâàëè ñâîèì åìêîñòíûì ñîïðîòèâëåíèåì âìåñòå ñ èíäóêòèâíûì ñîïðîòèâëåíèåì îáìîòîê ïðîñàäêó íàïðÿæåíèÿ â ñåòè, òî åñòü ñëåãêà ïðèáëèçèâ öåïü ê ðåçîíàíñó ìîæíî ïîäíÿòü óïàâøåå íàïðÿæåíèå äàæå ïîä íàãðóçêîé.
Ðåçîíàíñ òîêîâ
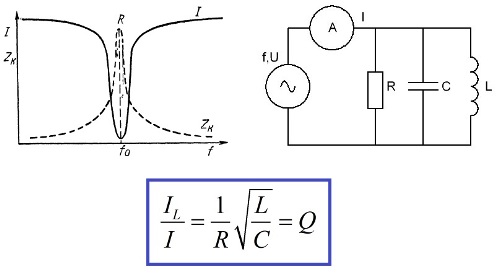
Êîãäà èñòî÷íèê ÝÄÑ, åìêîñòü, èíäóêòèâíîñòü è ñîïðîòèâëåíèå âêëþ÷åíû ìåæäó ñîáîé ïàðàëëåëüíî, òî ðåçîíàíñ â òàêîé öåïè íàçûâàåòñÿ ïàðàëëåëüíûì ðåçîíàíñîì èëè ðåçîíàíñîì òîêîâ. Õàðàêòåðíàÿ ÷åðòà ðåçîíàíñà òîêîâ çíà÷èòåëüíûå òîêè ÷åðåç åìêîñòü è èíäóêòèâíîñòü, ïî ñðàâíåíèþ ñ òîêîì èñòî÷íèêà.
Ïðè÷èíà ïîÿâëåíèÿ òàêîé êàðòèíû î÷åâèäíà. Òîê ÷åðåç àêòèâíîå ñîïðîòèâëåíèå ïî çàêîíó Îìà áóäåò ðàâåí U/R, ÷åðåç åìêîñòü U/XC, ÷åðåç èíäóêòèâíîñòü U/XL, è ñîñòàâèâ îòíîøåíèå IL ê I ìîæíî íàéòè âåëè÷èíó äîáðîòíîñòè Q. Òîê ÷åðåç èíäóêòèâíîñòü áóäåò â Q ðàç áîëüøå òîêà èñòî÷íèêà, òàêîé æå òîê áóäåò òå÷ü êàæäûå ïîë ïåðèîäà â êîíäåíñàòîð è èç íåãî.
Òî åñòü ðåçîíàíñ òîêîâ ïðèâîäèò ê âîçðàñòàíèþ òîêà ÷åðåç ðåàêòèâíûå ýëåìåíòû â Q ðàç, à ðåçîíàíñíàÿ ÝÄÑ áóäåò îãðàíè÷åíà ÝÄÑ èñòî÷íèêà, åãî âíóòðåííèì ñîïðîòèâëåíèåì è àêòèâíûì ñîïðîòèâëåíèåì öåïè R. Òàêèì îáðàçîì, íà ðåçîíàíñíîé ÷àñòîòå ñîïðîòèâëåíèå ïàðàëëåëüíîãî êîëåáàòåëüíîãî êîíòóðà ìàêñèìàëüíî.
Ïðèìåíåíèå ðåçîíàíñà òîêîâ
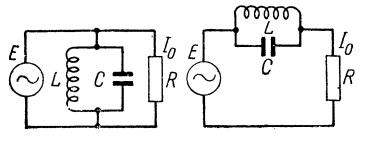
Àíàëîãè÷íî ðåçîíàíñó íàïðÿæåíèé, ðåçîíàíñ òîêîâ ïðèìåíÿåòñÿ â ðàçëè÷íûõ ôèëüòðàõ. Íî âêëþ÷åííûé â öåïü, ïàðàëëåëüíûé êîíòóð äåéñòâóåò íàîáîðîò, ÷åì â ñëó÷àå ñ ïîñëåäîâàòåëüíûì: óñòàíîâëåííûé ïàðàëëåëüíî íàãðóçêå, ïàðàëëåëüíûé êîëåáàòåëüíûé êîíòóð ïîçâîëèò òîêó ðåçîíàíñíîé ÷àñòîòû êîíòóðà ïðîéòè â íàãðóçêó, ïîñêîëüêó ñîïðîòèâëåíèå ñàìîãî êîíòóðà íà ñîáñòâåííîé ðåçîíàíñíîé ÷àñòîòå ìàêñèìàëüíî.
Óñòàíîâëåííûé ïîñëåäîâàòåëüíî ñ íàãðóçêîé, ïàðàëëåëüíûé êîëåáàòåëüíûé êîíòóð íå ïðîïóñòèò ñèãíàë ðåçîíàíñíîé ÷àñòîòû, ïîñêîëüêó âñå íàïðÿæåíèå óïàäåò íà êîíòóðå, à íà íàãðóçêó ïðèäåòñÿ ìèçåðíàÿ äîëÿ ñèãíàëà ðåçîíàíñíîé ÷àñòîòû.
Òàê, îñíîâíîå ïðèìåíåíèå ðåçîíàíñà òîêîâ â ðàäèîòåõíèêå ñîçäàíèå áîëüøîãî ñîïðîòèâëåíèÿ äëÿ òîêà îïðåäåëåííîé ÷àñòîòû â ëàìïîâûõ ãåíåðàòîðàõ è óñèëèòåëÿõ âûñîêîé ÷àñòîòû.
 ýëåêòðîòåõíèêå ðåçîíàíñ òîêîâ èñïîëüçóåòñÿ ñ öåëüþ äîñòèæåíèÿ âûñîêîãî êîýôôèöèåíòà ìîùíîñòè íàãðóçîê, îáëàäàþùèõ çíà÷èòåëüíûìè èíäóêòèâíûìè è åìêîñòíûìè ñîñòàâëÿþùèìè.
Íàïðèìåð, óñòàíîâêè êîìïåíñàöèè ðåàêòèâíîé ìîùíîñòè (ÊÐÌ) ïðåäñòàâëÿþò ñîáîé êîíäåíñàòîðû, ïîäêëþ÷àåìûå ïàðàëëåëüíî îáìîòêàì àñèíõðîííûõ äâèãàòåëåé è òðàíñôîðìàòîðîâ, ðàáîòàþùèõ ïîä íàãðóçêîé íèæå íîìèíàëüíîé.
Ê òàêèì ðåøåíèÿì ïðèáåãàþò êàê ðàç ñ öåëüþ äîñòèæåíèÿ ðåçîíàíñà òîêîâ (ïàðàëëåëüíîãî ðåçîíàíñà), êîãäà èíäóêòèâíîå ñîïðîòèâëåíèå îáîðóäîâàíèÿ äåëàåòñÿ ðàâíûì åìêîñòíîìó ñîïðîòèâëåíèþ ïîäêëþ÷àåìûõ êîíäåíñàòîðîâ íà ÷àñòîòå ñåòè, ÷òîáû ðåàêòèâíàÿ ýíåðãèÿ öèðêóëèðîâàëà ìåæäó êîíäåíñàòîðàìè è îáîðóäîâàíèåì, à íå ìåæäó îáîðóäîâàíèåì è ñåòüþ; ÷òîáû ñåòü îòäàâàëà ýíåðãèþ òîëüêî òîãäà, êîãäà îáîðóäîâàíèå íàãðóæåíî è ïîòðåáëÿåò àêòèâíóþ ìîùíîñòü.
Êîãäà æå îáîðóäîâàíèå ðàáîòàåò â õîëîñòóþ, ñåòü îêàçûâàåòñÿ ïîäêëþ÷åíà ïàðàëëåëüíî ðåçîíàíñíîìó êîíòóðó (âíåøíèå êîíäåíñàòîðû è èíäóêòèâíîñòü îáîðóäîâàíèÿ), êîòîðûé ïðåäñòàâëÿåò äëÿ ñåòè î÷åíü áîëüøîå êîìïëåêñíîå ñîïðîòèâëåíèå è ïîçâîëÿåò ñíèçèòüñÿ êîýôôèöèåíòó ìîùíîñòè.
Источник
Начнём с основных определений.
Определение 1
Резонанс — это явление, при котором частота колебаний какой-либо системы увеличивается колебаниями внешней силы.
Вынужденные колебания, источником которых является внешняя сила, увеличивают даже те колебания, амплитуда которых имеет довольно небольшие значения. Максимальный резонанс с наибольшей амплитудой возможен именно при совпадении частот внешнего воздействия и рассматриваемой системы.
Примером резонанса является раскачивание моста ротой солдат. Частота шага солдат, являющаяся по отношению к мосту примером вынужденных колебаний, при этом синхронизирована и может совпасть с собственной частотой колебаний моста. В результате мост может разрушиться.
Электрический резонанс в физике считается одним из распространенных в мире физических явлений, без которого было бы невозможным, например, телевидение и диагностика с помощью медицинских аппаратов.
Одними из наиболее полезных видов резонанса в электрической цепи являются:
- резонанс токов;
- резонанс напряжений.
Возникновение резонанса в электрической цепи
Замечание 1
Возникновению резонанса в электрической цепи способствует резкое увеличение амплитуды стационарных собственных колебаний системы при условии совпадения частоты внешней стороны воздействия и соответствующей колебательной резонансной частоты системы.
Схема $RLC$ представляет электрическую цепь с соединенными последовательным или параллельным образом элементами (резистора, индуктора, конденсатора). Название $RLC$ состоит из простых символов электрических элементов: сопротивления, емкости, индуктивности.
Векторная диаграмма последовательной $RLC$-цепи представлена в одной из трех вариаций:
- емкостной;
- активной;
- индуктивной.
В последней вариации резонанс напряжений возникает при условии нулевого сдвига фаз, и совпадении значений индуктивного и емкостного сопротивлений.
Резонанс напряжений
При последовательном соединении активного элемента $r$, емкостного $С$ и индуктивного $L$ в цепях переменного тока может возникать такое физическое явление, как резонанс напряжений. Колебания источника напряжения в этом случае будут равны по частоте колебаниям контура. При этом известна как полезность (например, в радиотехнике) этого явления, так и негативные последствия (для электрических установок большой мощности), например, при резком скачке напряжения в системах возможно возникновение неисправности или даже пожара.
Резонанс напряжений обычно достигается тремя способами:
- подбором индуктивности катушки;
- подбором емкости конденсатора;
- подбором угловой частоты $w_0$.
При этом все значения емкости, частоты и индуктивности определяются с использованием формул:
$L_0 = frac{1}{w^2C}$
$C_0 = frac{1}{w^2L}$
Частота $w_0$ считается резонансной. При условии неизменности в цепи и напряжения, и активного сопротивления $r$, сила тока при резонансе напряжения в ней окажется максимальной и равной:
$frac{U}{r}$
Это предполагает полную независимость силы тока от реактивного сопротивления цепи. В ситуации, когда реактивные сопротивления $XC = XL$ по своему значению будут превосходить активное сопротивление $r$, на зажимах катушки и конденсатора появится напряжение, существенно превосходящее напряжение на зажимах цепи.
Кратность превышения на зажимах емкостного и индуктивного элемента напряжения по отношению к сети определяется выражением:
$Q = frac{U_c0}{U}$
Величина $Q$ характеризует резонансные свойства контура, называясь при этом добротностью контура. Также резонансные свойства характеризуются величиной $frac{1}{Q}$, то есть — затуханием контура.
Резонанс токов через реактивные элементы
Резонанс токов появляется в электроцепях цепях переменного тока при условии параллельного соединения ветвей с разнохарактерными реактивными сопротивлениями. В резонансном режиме токов реактивная индуктивная проводимость цепи будет равнозначной ее собственной реактивной емкостной проводимости, т.е. $BL = BC$.
Колебания контура, частота которых имеет определённое значение, в данном случае совпадают по частоте с источником напряжения.
Простейшей электроцепью, в которой мы наблюдаем резонанс токов, считается цепь с параллельным соединением конденсатора с катушкой индуктивности.
Поскольку сопротивления реактивности равнозначны по модулю, амплитуды токов $I_c$ и $I_u$ будут одинаковыми и смогут достигать максимальной амплитуды. На основании первого закона Кирхгофа $IR$ равен току источника. Ток источника, иными словами, протекает только через резистор. При рассмотрении отдельного параллельного контура $LC$, на резонансной частоте его сопротивление оказывается бесконечно большим: $ZL = ZC$. При установлении гармонического режима с резонансной частотой, в контуре наблюдается обеспечение источником установившейся определенной амплитуды колебаний, а мощность источника тока при этом расходуется исключительно на пополнение потерь в активном сопротивлении.
Таким образом, у последовательной $RLC$ цепи импеданс оказывается минимальным на резонансной частоте и равным активному сопротивлению контура. В то же время, у параллельной $RLC$ цепи импеданс максимальный на резонансной частоте и считается равным сопротивлению утечки, фактически также активному сопротивлению контура. С целью обеспечения условий для резонанса силы тока или напряжения, требуется проверка электрической цепи для предопределения ее комплексного сопротивления или проводимости. Помимо этого, её мнимая часть должна приравниваться к нулю.
Применение явления резонанса
Хороший пример использования резонансного явления представляет электрический резонансный трансформатор, разработанный Николой Тесла ещё в 1891 году. Ученый проводил эксперименты на разных конфигурациях, состоящих в сочетании из двух, а зачастую и трех резонансных электроцепей.
Замечание 2
Термин «катушки Теслы» применяют к высоковольтным резонансным трансформаторам. Устройства используют при получении высокого напряжения, частоты переменного тока. Обычный трансформатор необходим для эффективной передачи энергии с первичной на вторичную обмотку, резонансный используется для временного хранения электроэнергии.
Устройство отвечает за управление воздушным сердечником настроенного резонансно трансформатора с целью получения высоких напряжений при малых значениях силы токов. Каждая обмотка обладает емкостью и функционирует в качестве резонансного контура. Для произведения наибольшего выходного напряжения первичный и вторичный контуры настраивают в резонанс друг с другом.
Источник
Резонанс в электрической цепи
Подробности
Просмотров: 505
«Физика – 11 класс»
В механике резонанс наблюдается в том случае, когда собственная частота колебаний системы совпадает с частотой изменения внешней силы.
Резонанс возможен и в электрической цепи, если эта цепь представляет собой колебательный контур, обладающий определенной собственной частотой колебаний.
При механике резонанс выражен при малом трении.
В электрической цепи роль коэффициента трения выполняет ее активное сопротивление R.
Наличие активного сопротивления в цепи приводит к превращению энергии тока во внутреннюю энергию проводника (проводник нагревается).
Поэтому резонанс в электрическом колебательном контуре выражен отчетливо при малом активном сопротивлении R.
Если активное сопротивление мало, то собственная циклическая частота колебаний в контуре:
Сила тока при вынужденных колебаниях достигает максимальных значений, когда частота переменного напряжения, приложенного к контуру, равна собственной частоте колебательного контура:
Резонансом в электрическом колебательном контуре называется явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.
Амплитуда силы тока при резонансе.
При резонансе в колебательном контуре создаются условия для поступления энергии от внешнего источника в контур.
Мощность в контуре максимальна в том случае, когда сила тока совпадает по фазе с напряжением.
В механике аналогично: при резонансе в механической колебательной системе внешняя сила (аналог напряжения в цепи) совпадает по фазе со скоростью (аналог силы тока).
После включения внешнего переменного напряжения амплитуда колебаний силы тока нарастает постепенно, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией, поступающей в контур за это же время:
тогда:
ImR = Um
Отсюда амплитуда установившихся колебаний силы тока при резонансе определяется уравнением
При R → 0 резонансное значение силы тока неограниченно возрастает: (Im)рез → ∞.
Наоборот, с увеличением R максимальное значение силы тока уменьшается.
Зависимость амплитуды силы тока от частоты при различных сопротивлениях (R1 < R2 < R3):

Одновременно с увеличением силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке индуктивности.
Эти напряжения при малом активном сопротивлении во много раз превышают внешнее напряжение.
Использование резонанса в радиосвязи
Явление электрического резонанса используется в радиосвязи.
На явлении резонанса основана вся радиосвязь.
Радиоволны от различных передающих станций возбуждают в антенне радиоприемника переменные токи различных частот, так как каждая передающая радиостанция работает на своей частоте.
С антенной индуктивно связан колебательный контур.

Из-за электромагнитной индукции в контурной катушке возникают переменные ЭДС соответствующих частот и вынужденные колебания силы тока тех же частот.
Но только при резонансе колебания силы тока в контуре и напряжения в нем будут значительными, т. е. из колебаний различных частот, возбуждаемых в антенне, контур выделяет только те, частота которых равна его собственной частоте.
Настройка контура на нужную частоту ω0 осуществляется путем изменения емкости конденсатора.
В этом обычно состоит настройка радиоприемника на определенную радиостанцию.
Необходимость учета возможности резонанса в электрической цепи
Если цепь не рассчитана на работу в условиях резонанса, то его возникновение может привести к аварии.
Чрезмерно большие токи могут перегреть провода.
Большие напряжения приводят к пробою изоляции.
Итак,
при вынужденных электромагнитных колебаниях возможен резонанс — резкое возрастание амплитуды колебаний силы тока и напряжения при совпадении частоты внешнего переменного напряжения с собственной частотой колебаний.
Источник: «Физика – 11 класс», учебник Мякишев, Буховцев, Чаругин
Электромагнитные колебания. Физика, учебник для 11 класса – Класс!ная физика
Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях —
Аналогия между механическими и электромагнитными колебаниями —
Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний —
Переменный электрический ток —
Активное сопротивление. Действующие значения силы тока и напряжения —
Конденсатор в цепи переменного тока —
Катушка индуктивности в цепи переменного тока —
Резонанс в электрической цепи —
Генератор на транзисторе. Автоколебания —
Краткие итоги главы
Источник
