Правильно ли построено следующее умозаключение все учебники полезны

1. Простой категорический силлогизм
Наиболее распространенной и важной формой опосредованного умозаключения из простых атрибутивных суждений выступает простой категорический силлогизм (от греч. syllogismos — умозаключение, выведение). Приводившийся выше пример с Сократом и есть классический пример такого силлогизма.
Структура простого категорического силлогизма. Он называется простым именно потому, что состоит всего из двух посылок, особым образом связанных между собой, и заключения.
В свою очередь, посылки и заключение, будучи суждениями, состоят из терминов, тоже определенным образом соотносящихся друг с другом. Принципиально важно отметить, что их всего три: меньший, больший и средний.
Меньшим термином называется субъект заключения. Поэтому он обозначается буквой «S».
Б?льшим термином именуется предикат заключения (буква «Р»).
Средний термин не входит в заключение, но входит в обе посылки, обеспечивая логическую связь между ними, выступая их посредствующим звеном и тем самым делая возможным само заключение. Обозначается буквой «М» (от лат. medius — средний).
Посылка, в которую входит больший термин, называется большей.
Посылка, включающая в себя меньший термин, — меньшая.
Вся эта структура может быть наглядно представлена на примере:
Все люди (М) смертны (Р). (Б?льшая посылка)
Сократ (S) — человек (М). (Меньшая посылка)
Следовательно, Сократ (S) смертен (Р). (Заключение)
Заметим, что все значение подобного силлогизма, который кажется ученически тривиальным и который люди до поры до времени не склонны относить к себе, обнаруживается (как это с огромной художественной силой показал Л.Толстой в повести «Смерть Ивана Ильича») лишь на смертном одре.
Аксиома силлогизма. Отражением многовековой практики мышления людей, миллиардного повторения одной и той же мыслительной конструкции служит аксиома силлогизма. В зависимости от того, рассматриваются ли посылки в объемном или содержательном плане, различаются две ее формулировки.
1. Dictum de omni et de nullo (буквально: сказанное обо всем и ни об одном): все, что утверждается или отрицается о классе предметов в целом, утверждается или отрицается и о части или отдельном элементе этого класса.
2. Nota notae est nota rei (признак признака есть признак самой вещи).
В современной логической литературе обе формулировки подвергаются критике; последняя считается даже элементарно ошибочной; но сама аксиома в целом сохраняет известный рациональный смысл. Более того, она составляет исходную логическую основу, на которой выстраивается грандиозное и стройное здание всей силлогистики.
Общие правила простого категорического силлогизма. Построение простого категорического силлогизма подчиняется ряду общих правил, без соблюдения которых даже из истинных посылок нельзя с логической необходимостью получить истинное заключение. Всего таких правил семь: три из них — это правила терминов, а четыре — правила посылок.
Каковы прежде всего правила терминов?
1. В силлогизме должно быть только три термина (S, Р и М). Нарушение этого правила ведет к логической ошибке, которая называется «quaternio terminorum» («учетверение терминов»). Так, из того, что «Собака бегает по двору», а «Кошка сидит на заборе», никакого вывода не получится. Здесь налицо четыре разных термина — два субъекта и два предиката. Среднего термина, который связывал бы оба суждения, нет.
Логическая ошибка «учетверение терминов» часто носит завуалированный характер. Это может быть связано с употреблением омонимов (т.е. одного и того же слова в разных значениях). Например, слово «закон» означает и объективную связь между предметами, и юридическое установление. Поэтому если мы построим силлогизм, где это слово выражает средний термин, то вытекающего отсюда с логической необходимостью вывода не получится.
Например:
Все законы объективны, т.е. не зависят от людей.
Конституция России — закон.
Следовательно, Конституция России не зависит от людей.
Нелепость получается именно из-за «учетверения терминов».
2. Средний термин должен быть распределен хотя бы в одной из посылок. Если это правило нарушается, то связь между большим и меньшим терминами будет неопределенной. Значит, и вывод из посылок не может следовать с логической необходимостью.
Все художники (Р) тонко чувствуют природу (М).
Петров (S) тонко чувствует природу (М).
Следовательно, Петров (S) — художник (P).
Вывод неопределенный, так как Петров может и не быть художником. Причина неопределенности в том, что средний термин (М), занимающий место предиката и в большей, и в меньшей посылках, не распределен, так как обе они утвердительные, а в утвердительных суждениях предикат, как правило, не распределен. Покажем соотношение терминов на круговой схеме:
3. Если больший или меньший термины не распределены в посылках, то они не могут быть распределены и в заключении.
Например:
Все учебники (М) полезны (Р).
Все учебники (М) — книги (S).
Следовательно, некоторые книги (S) полезны (Р).
А почему в этом случае нельзя сказать, что «Все книги полезны»? Суть в том, что субъект заключения («книги»), занимающий место предиката в меньшей посылке, не распределен, так как эта посылка утвердительная, а в утвердительных суждениях предикат, как правило, не распределен. Поэтому он не может быть взят во всем объеме и в заключении. См. круговую схему:
Нетрудно догадаться, что по этой же причине не распределен и предикат заключения.
Таковы правила терминов. А теперь о правилах посылок.
1. Из двух отрицательных посылок определенного вывода сделать нельзя. Хотя бы одна из них должна быть утвердительным суждением. Например:
Стекло (М) не проводит электричества (Р).
Резина (S) — не стекло (М).
Следовательно, резина (S) проводит электричество (P).
Вывод ложный. Если же вместо «резины» подставить, например, «железо», то он окажется истинным. В чем причина неопределенности вывода? В том, что при отрицательных посылках средний термин не может связать субъект и предикат. См. схему:
2. Если одна из посылок отрицательная, то и вывод будет отрицательным. Например:
Всякое преступление (Р) есть правонарушение (М).
Моральный проступок (S) не есть правонарушение (М).
Следовательно, моральный проступок (S) не есть преступление (Р).
См. схему:
3. Из двух частных посылок определенного вывода сделать нельзя. Хотя бы одна из посылок должна быть общим суждением.
Например:
Некоторые депутаты Госдумы (М) — юристы (Р).
Некоторые артисты (S) — депутаты Госдумы (М).
Следовательно, некоторые артисты (S) — юристы (Р)
А может быть, «ни один»? А почему не «все»?
См. схему:
4. Если одна из посылок частная, то и вывод будет частным. Например:
Некоторые пенсионеры (Р) — работающие (М).
Все работающие (М) получают заработную плату (S).
Следовательно, некоторые получающие заработную плату (S) — пенсионеры (Р).
См. схему:
Фигуры и модусы простого категорического силлогизма. Простой категорический силлогизм имеет свои разновидности, которые называются фигурами силлогизма. Они различаются положением среднего термина (М) в посылках. Таких фигур четыре.
Первая фигура характеризуется тем, что средний термин занимает место субъекта в большей посылке и место предиката — в меньшей. Приведем соответственно ее графическое изображение и пример.
Всякое преступление (М) есть правонарушение (Р).
Кража (S) есть преступление (М).
Следовательно, кража (S) есть правонарушение (Р).
Во второй фигуре средний термин занимает место предиката в большей и меньшей посылках.
Все юристы (Р) знают логику (М).
Павлов (S) не знает логики (М).
Следовательно, Павлов (S) — не юрист (Р).
Третья фигура отличается тем, что средний термин занимает здесь место субъекта в большей и меньшей посылках.
Все учебники (М) полезны (Р).
Все учебники (М) — книги (S).
Следовательно, некоторые книги (S) полезны (Р).
Четвертой фигуре свойственно то, что средний термин занимает здесь место предиката в большей посылке и место субъекта — в меньшей.
Некоторые пенсионеры (Р) — работающие (М).
Все работающие (М) получают зарплату (S).
Следовательно, некоторые получающие зарплату (S) — пенсионеры (Р).
Каждая фигура тоже имеет свои разновидности, которые называются модусами (от лат. modus — способ, образ). Они различаются количеством и качеством суждений, составляющих посылки. Каждая из посылок может быть общеутвердительной (А), общеотрицательной (Е), частноутвердительной (I) и частноотрицательной (О). Поэтому в одной фигуре возможно 16 модусов (4×4). Так, если большая посылка — общеутвердительная (А), то могут быть следующие модусы: АА, АЕ, AI, АО. Если большая посылка — общеотрицательная (Е), то возможны модусы ЕА, ЕЕ, EI, ЕО. Если большая посылка — частноутвердительная (I), то модусы будут IA, IE, II, IO. Наконец, если большая посылка — частноотрицательная (О), то могут быть модусы ОА, ОЕ, OI, OO.
Таким образом, в четырех фигурах соответственно будет 64 модуса (16?4). Но правильные из них — только 19 модусов.
Запишем их вместе с заключениями:
по первой фигуре — AAA, ЕАЕ, АII, ЕIO;
по второй фигуре — ЕАЕ, АЕЕ, ЕIO, АОО;
по третьей фигуре — AAI, IAI, АII, ЕАО, ОАО, ЕIO
и, наконец, по четвертой — AAI, АЕЕ, IAI, ЕАО, ЕIO.
Почему только эти 19 модусов являются правильными? Потому что именно они подчиняются общим правилам простого категорического силлогизма. Остальные же так или иначе не подчиняются. Например, модус ЕЕ — неправильный, так как обе посылки отрицательные, а из них определенного вывода сделать нельзя. Или модус II: в нем обе посылки частные.
Специальные правила фигур силлогизма. Каждая из фигур имеет особые, специальные правила, вытекающие из общих.
Правила первой фигуры. Большая посылка должна быть общим суждением, меньшая посылка — утвердительным. Начнем с меньшей. Если меньшая посылка — отрицательная, то и вывод, согласно одному из общих правил силлогизма, будет отрицательным. Но в отрицательных суждениях предикат всегда распределен. Следовательно, согласно одному из правил терминов, он должен быть распределен и в большей посылке. А он может быть распределен в ней лишь в том случае, если эта посылка отрицательная. Но это противоречит одному из общих правил о том, что из двух отрицательных посылок определенного вывода сделать нельзя. Значит, меньшая посылка не может быть отрицательной. Значит, она должна быть утвердительным суждением.
А почему большая посылка должна быть непременно общей? Если, как установлено, меньшая посылка — утвердительная, то средний термин, занимающий в ней место предиката, не распределен. Следовательно, согласно одному из общих правил терминов, он должен быть распределен в большей. А так как он занимает в ней место субъекта, то, значит, она должна быть общим суждением.
Вспомним, что в первой фигуре возможны следующие модусы:
АА
ЕА
IA
ОА
АЕ
ЕЕ
IE
ОЕ
AI
EI
II
OI
АО
ЕО
IO
OO
Вычеркнем вначале все те, которые не соответствуют первому правилу первой фигуры, а затем те, которые не соответствуют второму правилу. Какие же останутся? АА, ЕА, AI, EI. А какие будут заключения? В соответствии с общими правилами силлогизма — ААА, ЕАЕ, АII, ЕIO.
Какое значение имеют умозаключения по первой фигуре простого категорического силлогизма? Без преувеличения — огромное. Это наиболее распространенная и богатая форма силлогизма. На ее основе происходит типичное для дедукции применение какого-либо общего положения к частному (или единичному) случаю. Вспомним классическое: «Все люди смертны. Сократ — человек». Первая фигура дает самые различные заключения: А, Е, I, О.
Ее часто используют в юридической практике, когда на основании общей нормы, — статьи какого-либо кодекса — делается вывод о конкретном факте. Например: «Хищение в особо крупных размерах наказывается по статье такой-то. Данное хищение — в особо крупном размере. Следовательно, оно наказывается по статье такой-то».
Правила второй фигуры. Большая посылка должна быть общим суждением, одна из посылок — отрицательным. Естественно, что по второй фигуре заключение всегда носит отрицательный характер. Значение умозаключений по второй фигуре тоже велико. Она используется в тех случаях, когда частный случай не подходит под общее правило. Например, в юридической практике — когда требуется доказать чью-либо невиновность.
Правила третьей фигуры. Меньшая посылка должна быть утвердительным суждением, заключение — частным. Третья фигура — сравнительно редкая в практике мышления.
Правила четвертой фигуры. Если большая посылка — утвердительное суждение, то меньшая посылка должна быть общим. Если одна из посылок отрицательное суждение, то большая должна быть общим. Заключение по четвертой фигуре носит в значительной мере искусственный характер. Вспомним пример с работающими пенсионерами:
Некоторые пенсионеры (Р) — работающие (М).
Все работающие (М) получают зарплату (S).
Следовательно, некоторые получающие зарплату (S) — пенсионеры (Р).
Естественнее было бы, конечно, сказать: «Некоторые пенсионеры получают зарплату».
Рассмотренные выше качественные различия между фигурами силлогизма на самом деле относительны. При определенных условиях силлогизм одной фигуры может превращаться в силлогизм другой.
Особое значение имеет здесь логическая операция, которая называется сведением всех фигур силлогизма к первой фигуре, поскольку она является наиболее употребительной и важной. Покажем это на примере силлогизма третьей фигуры, уже приводившемся нами:
Все учебники (М) полезны (Р).
Все учебники (М) — книги (S).
Следовательно, некоторые книги (S) полезны (Р).
Подвергнем меньшую посылку операции обращения: «Все учебники — книги» — «Некоторые книги — учебники». В итоге получим то же самое заключение, но уже по первой фигуре:
Все учебники (М) полезны (Р).
Некоторые книги (S) — учебники (М).
Следовательно, некоторые книги (S) полезны (Р).
Сокращенная форма простого категорического силлогизма. Энтимема. Простой категорический силлогизм может быть полным и сокращенным.
В практике мышления далеко не всегда он может облекаться в полную, т. е. развернутую, языковую форму — с большей и меньшей посылками, заключением.
Нередко он принимает сокращенную форму, т. е. в нем опускается либо одна из посылок, либо заключение. Такой сокращенный категорический силлогизм называется энтимемой (от греч. «в уме»).
Существует три разновидности энтимемы:
1) силлогизм с пропущенной большей посылкой. Например: «Петров — адвокат. Следовательно, он юрист». Здесь подразумевается очевидная большая посылка: «Все адвокаты — юристы», поэтому она опускается;
2) энтимема с пропущенной меньшей посылкой. Например: «Все адвокаты — юристы. Следовательно, Петров юрист». Предполагается, что «Петров — адвокат»;
3) энтимема с пропущенным заключением. Например: «Все адвокаты — юристы. Петров — адвокат». Предполагается, что «следовательно, он юрист».
Значение энтимем состоит в том, что с их помощью достигается краткость, лаконичность речи. Кроме того, они побуждают слушателя или читателя мыслить, думать. Вот почему энтимемы довольно широко используются в устной и письменной речи. Так, древний афоризм: «Юпитер, ты сердишься, значит, ты неправ» — это энтимема. Здесь подразумевается, а поэтому опущена, большая посылка: «Всякий, кто сердится, неправ». Восстановим весь силлогизм полностью:
Всякий, кто сердится, неправ.
Юпитер сердится.
Следовательно, Юпитер неправ.
Подобную энтимему представляет замечательно краткое и сильное высказывание А. Пушкина о Е. Баратынском: «Оригинален, ибо мыслит». Здесь тоже опущена большая посылка. Восстановим полный силлогизм:
Тот, кто мыслит, оригинален.
Баратынский мыслит.
Следовательно, Баратынский оригинален.
Еще пример. «Все это говорят, а что говорят все, должно быть правдой». Пропущено заключение: «Следовательно, это правда».
Или как сказано у поэта: «Я где боль: а боль — везде». Восстановим полностью силлогизм:
Боль везде.
Я — где боль.
Следовательно, я везде.
Для чего необходимо восстанавливать полный силлогизм из энтимемы? Чтобы проверить ее правильность. Как это делается? Покажем всю процедуру на примере: «Он, должно быть, очень невежественный человек, поскольку отвечает на все вопросы, которые ему задают». Сначала находим заключение. Оно, как мы помним, стоит после слова «следовательно» и ему подобных либо перед словами «потому что» и их аналогами. В нашем примере заключением будет: «Он, должно быть, очень невежественный человек», так как стоит перед словом «поскольку». Определяем структуру этого суждения, т.е. находим в нем субъект и предикат. Субъект — «он», предикат — «невежественный человек». По субъекту или предикату заключения устанавливаем характер имеющейся налицо посылки: «Он отвечает на все вопросы…» В ней находится субъект заключения, следовательно, это меньшая посылка. По предикату заключения и среднему термину, который входит в меньшую посылку, восстанавливаем опущенную большую посылку: «Тот, кто отвечает на все вопросы, должно быть, очень невежественный человек». Получаем полный силлогизм:
Тот, кто отвечает на все вопросы, невежественный человек.
Он отвечает на все вопросы, которые ему задают.
Следовательно, он невежественный человек.
Проверим правильность этого силлогизма. Он построен по первой фигуре, оба правила этой фигуры (см. выше) соблюдены. Значит, этот силлогизм правильный. Его можно проверить также с помощью круговой схемы:
Источник

В этом уроке мы, наконец, переходим к теме, которая составляет ядро любого рассуждения и любой логической системы – умозаключениям. В четвёртом уроке мы говорили, что рассуждение – это совокупность суждений или высказываний. Очевидно, что такое определение не полно, ведь оно ничего не говорит о том, почему вдруг какие-то разные высказывания оказались рядом. Если дать более точное определение, то рассуждение – это процесс обоснования какого-либо высказывания с помощью его последовательного вывода из других высказываний. Этот вывод чаще всего осуществляется в форме умозаключений.
Содержание:
- Критерии истинности умозаключений
- Умозаключения по логическому квадрату
- Операция обращения
- Игра “Подбери ключ”
- Упражнения
- Проверочные вопросы на усвоение материала
Умозаключение – это непосредственный переход от одного или нескольких высказываний А1, А2, …, Аn к высказыванию В. А1, А2, …, Аn называют посылками. Посылка может быть одна, их может быть две, три, четыре, в принципе – сколько угодно. В посылках содержится известная нам информация. В – это заключение. В заключении находится уже новая информация, которую мы извлекли из посылок с помощью специальных процедур. Эта новая информация уже содержалась в посылках, но в скрытом виде. Так вот задача умозаключения сделать это скрытое явным. Кроме того, иногда посылки называют аргументами, а заключение – тезисом, а само умозаключение в этом случае называют обоснованием. Разница между умозаключением и обоснованием состоит в том, что в первом случае, мы не знаем, к какому заключению мы придём, а во втором – тезис нам уже известен, мы просто хотим установить его связь с посылками-аргументами.
В качестве иллюстрации умозаключения можно взять рассуждения Эркюля Пуаро из «Убийства в восточном экспрессе» Агаты Кристи:
Перебрав в уме еще раз показания пассажиров, я пришел к весьма любопытным результатам. Для начала возьмем показания мистера Маккуина. Первая беседа с ним не вызвала у меня никаких подозрений. Но во время второй он обронил небезынтересную фразу. Я сообщил ему, что мы нашли записку, в которой упоминается о деле Армстронгов. Он сказал: «А разве…» – осекся и, помолчав, добавил: «Ну это самое… неужели старик поступил так опрометчиво?…»
Но я почувствовал, что он перестроился на ходу. Предположим, он хотел сказать: «А разве ее не сожгли?» Следовательно, Маккуин знал и о записке, и о том, что ее сожгли, или, говоря другими словами, он был убийцей или пособником убийцы.
Логики записывают умозаключения следующим образом:
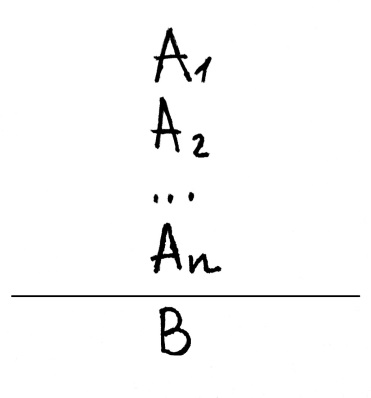
Над чертой располагаются посылки, под чертой – заключение, а сама черта обозначает отношение логического следования.
Критерии истинности умозаключений
Также как и для суждений, для умозаключений существуют определённые условия их истинности. При определении, истинное умозаключение или ложное, нужно обращать внимание на два аспекта. Первый аспект – это истинность посылок. Если хотя бы одна из посылок ложна, то и сделанное заключение тоже будет ложным. Поскольку заключение – это та информация, которая была скрыта в посылках и которую мы просто извлекли на свет, то из неверных посылок невозможно случайно получить верный вывод. Это можно сравнить с попыткой сделать бифштекс из моркови. Наверное, моркови можно придать цвет и форму бифштекса, но внутри всё равно будет морковь, а не мясо. Никакие кулинарные операции не преобразуют одно в другое.
Второй аспект – это правильность самого умозаключения с точки зрения его логической формы. Дело в том, что истинность посылок – это важное, но недостаточное условие для того, чтобы заключение было правильным. Нередки ситуации, когда посылки истинны, но заключение неверно. В качестве примера неправильного умозаключения при истинности посылок можно привести умозаключение голубки из «Алисы в стране чудес» Кэрролла. Голубка обвиняет Алису, в том, что она не змея. Вот как она приходит к этому выводу:
Змеи едят яйца.
Девочки едят яйца.
Значит, девочки – это змеи.
Хотя посылки правильные, заключение абсурдно. Умозаключение в целом сделано неверно. Чтобы избежать подобных ошибок, логики выявили такие умозаключения, логические формы которых при истинности посылок гарантируют истинность заключения. Их принято называть правильными умозаключениями. Таким образом, чтобы умозаключение было сделано верно, нужно следить за истинностью посылок и за правильностью самой формы умозаключения.
Мы рассмотрим различные формы правильных умозаключений на примере силлогистики. В этом уроке мы разберём самые простые однопосылочные заключения. В следующем уроке – более сложные заключения: силлогизмы, энтимемы, многопосылочные заключения.
Умозаключения по логическому квадрату
Чтобы было легче запомнить, какие именно типы умозаключений возможны между категорическими атрибутивными высказываниями, логики придумали специальный логический квадрат, изображающий отношения между ними. Поэтому некоторые однопосылочные умозаключения также называют умозаключениями по логическому квадрату. Посмотрим на этот квадрат:
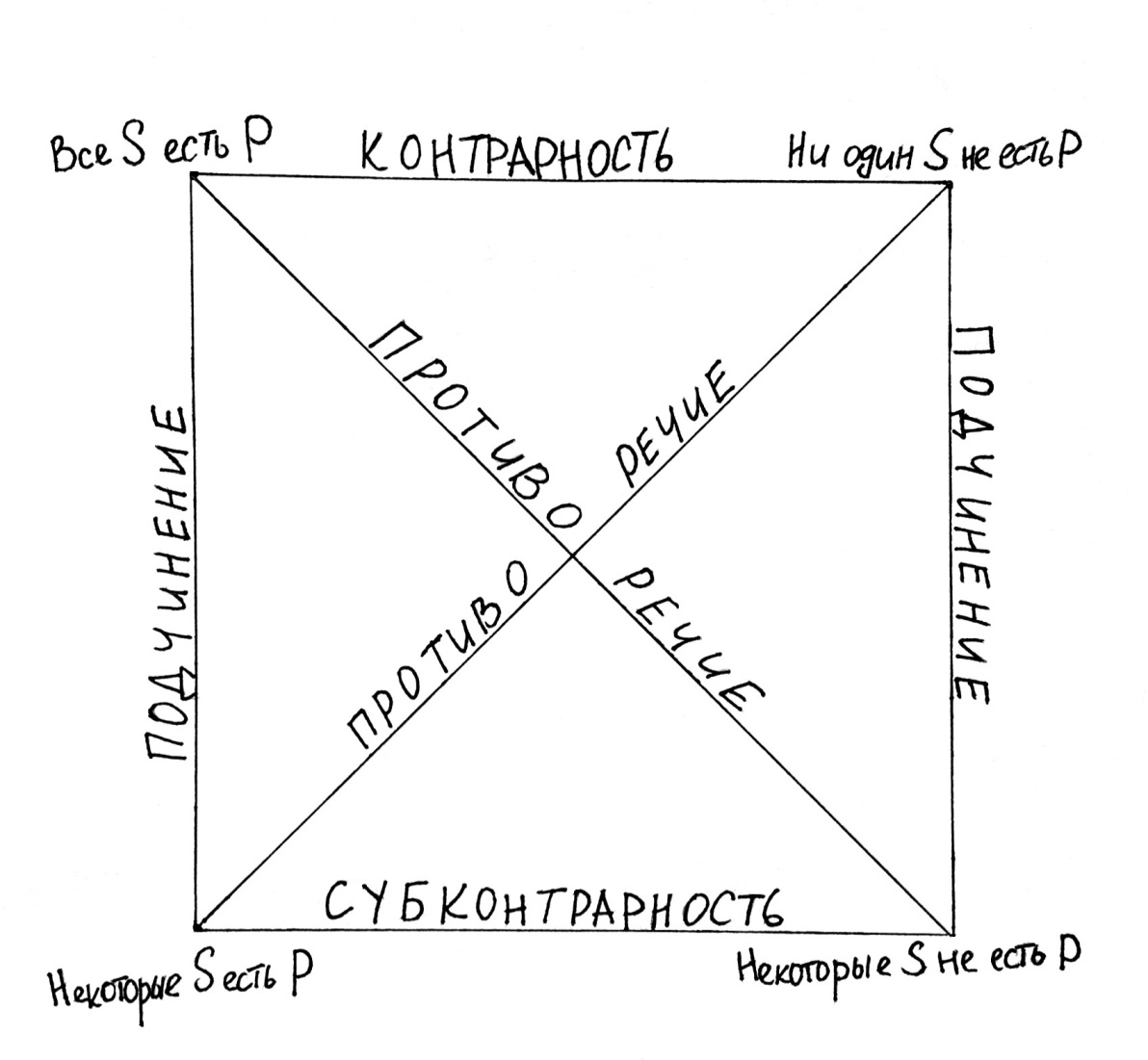
Начнём с отношений подчинения. Мы уже сталкивались с ними в четвёртом уроке, когда рассматривали условия истинности для частно-утвердительных и частно-отрицательных высказываний. Мы говорили, что из высказывания «Все S есть P» будет логичным вывести высказывание «Некоторые S есть P», а из высказывания «Ни один S не есть P» – «Некоторые S не есть P». Таким образом, возможны следующие типы умозаключений:
- Все S есть P
- Некоторые S есть P
- Все птицы имеют клюв. Следовательно, некоторые птицы имеют клюв.
- Ни один S не есть P
- Некоторые S не есть P
- Ни один гусь не хочет быть пойман и зажарен. Следовательно, некоторые гуси не хотят быть пойманными и зажаренными.
Кроме того, по правилу контрапозиции из отношений подчинения можно вывести ещё два правильных умозаключения. Правило контрапозиции – это логический закон, который гласит: если из высказывания А следует высказывание В, то из высказывания «неверно, что В» будет следовать высказывание «неверно, что А». Вы можете попробовать проверить этот закон с помощью таблицы истинности. Итак, будут верны и следующие умозаключения по контрапозиции:
- Неверно, что некоторые S есть P
- Неверно, что все S есть P
- Неверно, что некоторые автомобили не имеют колёс. Поэтому неверно, что все автомобили не имеют колёс.
- Неверно, что некоторые S не есть P
- Неверно, что все S не есть P
- Неверно, что некоторые вина не являются спиртными напитками. Таким образом, неверно, что все вина не являются спиртными напитками.
Отношение контрарности (противоположности) означает, что высказывания типа «Все S есть P» и «Ни один S не есть P» не могут быть одновременно истинными, но они могут быть одновременно ложными. Это хорошо видно из таблицы истинности для категоричных атрибутивных высказываний, которую мы построили в прошлом уроке. Отсюда можно вывести так называемый закон контрарного противоречия: Неверно, что все S есть P и в то же время ни один S не есть P.
По закону контрарного противоречия будут истинными следующие виды умозаключений:
- Все S есть P
- Неверно, что ни один S не есть P
- Все яблоки – это фрукты. Следовательно, неверно, что ни одно яблоко не является фруктом.
- Ни один S не есть P
- Неверно, что все S есть P
- Ни один кит не умеет летать. Поэтому неверно, что все киты умеют летать.
Отношения субконтрарности (подпротивоположности) означают, что высказывания типа «Некоторые S есть P» и «Некоторые S не есть P» не могут быть одновременно ложными, хотя могут быть одновременно истинными. На этом основании может быть сформулирован закон субконтрарного исключённого третьего: Некоторые S не есть P или Некоторые S есть P.
- Согласно этому закону правильными будут следующие умозаключения:
- Неверно, что некоторые S есть P
- Некоторые S не есть P
- Неверно, что некоторые продукты полезны для здоровья. Поэтому некоторые продукты не полезны для здоровья.
- Неверно, что некоторые S не есть P
- Некоторые S есть P
- Неверно, что некоторые ученики из нашего класса не являются двоечниками. Таким образом, некоторые ученики из нашего класса являются двоечниками.
Отношения противоречия (контрадикторности) говорят о том, что высказывания, находящиеся в них, не могут быть одновременно истинными или ложными. На основании этих отношений можно сформулировать два закона противоречия и два закона исключённого третьего. Первый закон противоречия: Неверно, что все S есть P и некоторые S не есть P. Второй закон противоречия: Неверно, что ни один S не есть P и некоторые S есть P. Первый закон исключённого третьего: Все S есть P или некоторые S не есть P. Второй закон исключённого третьего: Ни один S не есть P или некоторые S есть P.
На этих законах строятся умозаключения следующих видов:
- Все S есть P
- Неверно, что некоторые S не есть P
- Все дети нуждаются в заботе. Следовательно, неверно, что некоторые дети не нуждаются в заботе.
- Некоторые S не есть P
- Неверно, что все S есть P
- Некоторые книги не являются скучными. Поэтому, неверно, что все книги являются скучными.
- Неверно, что все S есть P
- Некоторые S не есть P
- Неверно, что все сотрудники нашей фирмы усердно работают. Таким образом, некоторые сотрудники нашей фирмы не работают усердно.
- Неверно, что некоторые S не есть P
- Все S есть P
- Неверно, что некоторые зебры не имеют полосок на коже. Следовательно, все зебры имеют полоски на коже.
- Ни один S не есть P
- Неверно, что некоторые S есть P
- Ни одна картина в этом зале не относится к XX веку. Поэтому неверно, что некоторые картины в этом зале относятся к XX веку.
- Некоторые S есть P
- Неверно, что ни один S не есть P
- Некоторые студенты занимаются спортом. Таким образом, неверно, что ни один студент не занимается спортом.
- Неверно, что ни один S не есть P
- Некоторые S есть P
- Неверно, что ни один учёный не интересуется искусством. Следовательно, некоторые учёные интересуются искусством.
- Неверно, что некоторые S есть P
- Ни один S не есть P
- Неверно, что некоторые коты курят сигары. Таким образом, ни один кот не курит сигары.
Как вы, скорее всего, заметили во всех этих умозаключениях, высказывания над чертой и под чертой несут одну и ту же информацию, просто поданную в разной форме. Важная деталь заключается в том, что смысл одних из этих высказываний воспринимается легко и интуитивно, в то время как смысл других тёмен, и над ними порой приходится поломать голову. Например, смысл утвердительных высказываний воспринимается легче, чем смысл отрицательных высказываний, смысл высказываний с одним отрицанием более понятен, чем смысл высказываний с двумя отрицаниями. Таким образом, основное назначение умозаключений по логическому квадрату состоит в том, чтобы привести сложные для восприятия, непонятные высказывания к наиболее простой и ясной форме.
Операция обращения
Ещё одним видом однопосылочных умозаключений является обращение. Это такой тип умозаключений, при которых субъект посылки совпадает с предикатом заключения, а субъект заключения совпадает с предикатом посылки. Грубо говоря, в заключении S и P просто меняются местами.
Прежде чем перейти к умозаключениям через обращение, построим таблицу истинности для высказываний, в которых P встанет на место субъекта, а S – на место предиката.
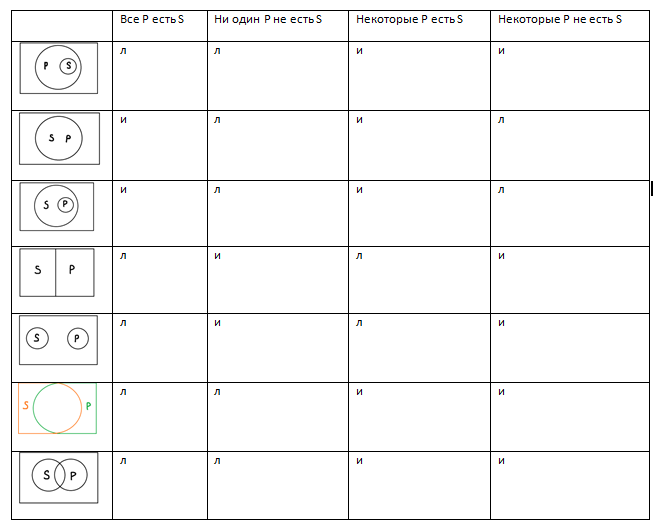
Сравните её с той таблицей, которую мы строили в прошлом уроке. Обращение, как и другие умозаключения, может быть правильным, только когда посылка и заключение одновременно истинны. При сравнении двух таблиц, вы увидите, что таких комбинаций не так уж и много.
Итак, существует два вида обращения: чистое и с ограничением. Чистое обращение происходит тогда, когда количественная характеристика не изменяется, то есть если в посылке было слово «все», то и в заключении тоже будет слова «все»/«ни один», если в посылке слово «некоторые», то и в заключении «некоторые. Соответственно, при обращении с ограничением количественная характеристика меняется: были «все», а стали «некоторые». Для высказываний типа «Ни один S не есть P» и «Некоторые S есть P» правильным будет следующее чистое обращение:
- Ни один S не есть P
- Ни один P не есть S
- Ни один человек не может выжить без воздуха. Следовательно, ни одно живое существо, способное выжить без воздуха, не является человеком.
- Некоторые S есть P
- Некоторые P есть S
- Некоторые змеи ядовиты. Поэтому, некоторые ядовитые существа – это змеи.
- Для высказываний типа «Все S есть P» и «Ни один S не есть P» верно обращение с ограничением:
- Все S есть P
- Некоторые P есть S
- Все пингвины – это птицы. Таким образом, некоторые птицы – это пингвины.
- Ни один S не есть P
- Некоторый P не есть S
- Ни один крокодил не ест зефир. Следовательно, некоторые существа, едящие зефир, не являются крокодилами.
- Высказывания типа «Некоторые S не есть P» вообще не обращаются.
Хотя обращения, как и умозаключения по логическому квадрату, это однопосылочные умозаключения, и мы точно также извлекаем всю новую информацию из имеющейся посылки, посылку и заключение в них уже нельзя назвать просто разными формулировками одной и той же информации. Полученная информация относится уже к другому субъекту, а потому она уже не кажется такой тривиальной.
Итак, в этом уроке мы начали рассматривать правильные виды умозаключений. Мы поговорили о самых простейших однопосылочных умозаключениях: умозаключениях по логическому квадрату и умозаключениях через обращение. Хотя эти умозаключения довольно просты и даже где-то тривиальны, люди повсеместно совершают в них ошибки. Понятно, что сложно удержать в памяти все виды правильных умозаключений, поэтому, когда вы будете выполнять упражнения или столкнётесь с необходимостью проверить или сделать однопосылочное умозаключение в реальной жизни, не бойтесь прибегать к помощи модельных схем и таблиц истинности. Они помогут вам проверить, всегда ли при истинности посылок заключение тоже истинное, а это главное для правильного умозаключения.
Упражнение «Подберите ключ»
В этой игре вам нужно создать ключ правильной формы. Для этого установите засечки нужной длины (от 1 до 3, 0 – быть не может), а затем нажмите кнопку «Попробовать». Вам будут даны 2 суждения, сколько засечек выбранной длины присутствуют в ключе (для простоты значение «наличие»), и сколько из выбранных находятся на своём месте (для простоты значение «на месте»). Скорректируйте своё решение и пробуйте, пока не подберёте ключ.
Упражнения
1
Сделайте все возможные умозаключения из следующих высказываний по логическому квадрату:
- Все медведи на зиму залегают в спячку.
- Неверно, что все люди завистливы.
- Ни один гном не достигает роста в два метра.
- Неверно, что ни один человек не был на Северном полюсе.
- Некоторые люди никогда не видели снега.
- Некоторые автобусы ходят по расписанию.
- Неверно, что некоторые слоны летали на луну.
- Неверно, что некоторые птицы не имеют крыльев.
2
Сделайте обращения с теми, высказываниями, с которыми это возможно:
- Никто ещё не построил машину времени.
- Некоторые официанты очень назойливы.
- Все профессионалы опытны в своём деле.
- Некоторые книги не имеют твёрдой обложки.
3
Проверьте, правильно ли сделаны следующие умозаключения:
- Некоторые кролики не носят белые перчатки. Следовательно, некоторые кролики носят белые перчатки.
- Неверно, что никто не был на Луне. Таким образом, некоторые люди были на Луне.
- Все люди смертны. Поэтому все смертные – это люди.
- Некоторые птицы не умеют летать. Следовательно, некоторые существа, не умеющие летать, это птицы.
- Ни один ягнёнок не имеет пристрастия к виски. Следовательно, ни одно существо, имеющее пристрастие к виски, не является ягнёнком.
- Некоторые морские животные млекопитающие. Таким образом, неверно, что ни одно морское животное не является млекопитающим.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Источник
