Полезная мощность от силы тока формула
Первое упоминание об электричестве встречается в опытах древнегреческого философа Фалеса. Именно он первым обнаружил, что предметы при трении притягиваются. Одноименный термин был введен в начале 17-го века английским физиком Гилбертом, после опытов, проведенных с магнитами. Отцом же науки об электричестве считается французский ученый Кулон – именно после открытия закона, получившего его имя, электротехника начала свою победную поступь, которая продолжается до сих пор. Этот закон утверждает, что два точечных заряда в безвоздушной среде взаимодействуют с силой, прямо пропорциональной их модулям и обратно – расстоянию между ними, возведенному в квадрат.
Выясним, что же представляет собой понятие электричество?
Если коротко, то это – направленное движение потока заряженных частиц. Тела, через которые они проходят, называются проводниками. Каждый проводник имеет определенное сопротивление электрическому току, которое раз
И, перед тем, как перейти к основным законам, несколько слов о заряженных частицах: они бывают, условно говоря, положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные – притягиваются.
А теперь, перейдем к главному.
Основа-основ науки об электричестве – закон Ома.
Эксперимент, который провел этот немецкий физик, привел его к следующему убеждению: сила тока I, проходящего через металлический проводник, пропорциональна напряжению на его концах, или I = U/R
Здесь напряжением называется разность, образно говоря, «давлений», созданных двумя точками электрической цепи. Измеряют его в вольтах. Электрический ток представляет собой число электронов, которые пропускает участок электрической цепи и измеряется в амперах. Сопротивлением считается свойство цепи помешать этому движению. В честь упомянутого физика, его измеряют в омах. Иначе говоря, проводник, через который проходит ток в 1 ампер при напряжении в 1 вольт, обладает сопротивлением в 1 ом.
Вся остальная электротехника «пляшет» от этого.
О мощности электрического тока
В физике мощностью считают скорость выполнения работы. Неважно, какой. Чем эта операция проводится быстрее, тем большей считается мощность того, кто ее исполняет, будь то человек, механическое устройство или что-то еще.
Так же и в случае с электрическим током: ее мощность представляет собой отношение работы, произведенной движущимися электрическими зарядами к промежутку времени, которое для этого понадобилось.
Проще говоря, для того, чтобы получить электрическую мощность в 1 ватт, когда источник тока имеет напряжение 1 вольт, необходимо пропустить через проводник ток в 1 ампер. Другими словами, мощность (P) можно посчитать, перемножив друг на друга электрическое напряжение и ток:
P = U*I.
Запомнив эту нехитрую формулу, на практике можно рассчитать мощность. Например, если известны значения тока и сопротивления, а о напряжении сведений нет, можем воспользоваться законом Ома, подставив в формулу вместо него I*R. Получится, что мощность равна квадрату электрического тока, помноженному на сопротивление.
Этот закон точно так же придет на помощь, если известны величины напряжения и сопротивления. В этом случае подставив вместо значения тока I = U/R, получим значение мощности, равное квадрату напряжения, поделенному на сопротивление.
Вот так – ничего сложного!
Определение и формула полезной мощности
Определение
Мощность – это физическая величина, которую использует как основную характеристику любого устройства, которое применяют
для совершения работы. Полезная мощность может быть использована для выполнения поставленной задачи.
Отношение работы ($Delta A$) к промежутку времени за которое она выполнена ($Delta t$) называют средней мощностью ($leftlangle Prightrangle $) за это время:
[leftlangle Prightrangle =frac{Delta A}{Delta t}left(1right).]
Мгновенной мощностью или чаще просто мощностью называют предел отношения (1) при $Delta tto 0$:
[P={mathop{lim }_{Delta tto 0} frac{Delta A}{Delta t} }=A'(t)left(2right).]
Приняв во внимание, что:
[Delta A=overline{F}cdot Delta overline{r }left(3right),]
где $Delta overline{r }$ – перемещение тела под действием силы $overline{F}$, в выражении (2) имеем:
[P={mathop{lim }_{Delta tto 0} left(frac{overline{F}cdot Delta overline{r }}{Delta t}right) }=overline{F}{mathop{lim }_{Delta tto 0} left(frac{Delta overline{r }}{Delta t}right)= }overline{F}cdot overline{v}left(4right),]
где $ overline{v}-$ мгновенная скорость.
Коэффициент полезного действия
При выполнении необходимой (полезной) работы, например, механической, приходится выполнять работу большую по величине, так как в реальности существуют силы сопротивления и часть энергии подвержена диссипации (рассеиванию). Эффективность совершения работы определяется при помощи коэффициента полезного действия ($eta $), при этом:
[eta =frac{P_p}{P}left(5right),]
где $P_p$ – полезная мощность; $P$ – затраченная мощность. Из выражения (5) следует, что полезная мощность может быть найдена как:
[P_p=eta P left(6right).]
Формула полезной мощности источника тока
Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:
[P=?I left(7right),]
где $?$ – ЭДС источника тока; $I$ – сила тока. При этом $P$ – полная мощность цепи.
Обозначим $U$ – напряжение на внешнем участке цепи, тогда формулу (7) представим в виде:
[P=?I=UI+I^2r=P_p+P_0left(8right),]
где $P_p=UI=I^2R=frac{U^2}{R}(9)$ – полезная мощность; $P_0=I^2r$ – мощность потерь. При этом КПД источника определяют как:
[eta =frac{P_p}{P_p+P_0}left(9right).]
Максимальную полезную мощность (мощность на нагрузке) электрический ток дает, если внешнее сопротивление цепи будет равно внутреннему сопротивлению источника тока. При этом условии полезная мощность равна 50% общей мощности.
При коротком замыкании (когда $Rto 0;;Uto 0$) или в режиме холостого хода $(Rto infty ;;Ito 0$) полезная мощность равна нулю.
Примеры задач с решением
Пример 1
Задание. Коэффициент полезного действия электрического двигателя равен $eta $ =42%. Какой будет его полезная мощность, если при напряжении $U=$110 В через двигатель идет ток силой $I=$10 А?
Решение. За основу решения задачи примем формулу:
[P_p=eta P left(1.1right).]
Полную мощность найдем, используя выражение:
[P=IUleft(1.2right).]
Подставляя правую часть выражения (1.2) в (1.1) находим, что:
[P_p=eta IU.]
Вычислим искомую мощность:
[P_p=eta IU=0,42cdot 110cdot 10=462 left(Втright).]
Ответ. $P_p=462$ Вт
Пример 2
Задание. Какова максимальная полезная мощность источника тока, если ток короткого замыкания его
равен $I_k$? При соединении с источником тока сопротивления $R$, по цепи (рис.1) идет ток силой $I$.
Решение. По закону Ома для цепи с источником тока мы имеем:
[I=frac{varepsilon}{R+r}left(2.1right),]
где $varepsilon$ – ЭДС источника тока; $r$ – его внутреннее сопротивление.
При коротком замыкании считаем, что сопротивление внешней нагрузки равно нулю ($R=0$), тогда сила тока короткого замыкания равна:
[I_k=frac{varepsilon}{r} left(2.2right).]
Максимальная полезная мощность в цепи рис.1 электрический ток даст, при условии:
[R=r left(2.3right).]
Тогда сила тока в цепи равна:
[I’=frac{varepsilon}{r+r}=frac{varepsilon}{2r}left(2.4right).]
Максимальную полезную мощность найдем, используя формулу:
[P_{p max}={I’}^2r={left(frac{varepsilon}{2r}right)}^2cdot r=frac{varepsilon^2}{4r}=frac{varepsilon^2}{4R}left(2.5right).]
Мы получили систему из трех уравнений с тремя неизвестными:
[left{ begin{array}{c}
I’=frac{varepsilon}{2r}, \
I_k=frac{varepsilon}{r}, \
P_{p max}={left(I’right)}^2r end{array}
left(2.6right).right.]
Используя первое и второе уравнения системы (2.6) найдем $I’$:
[frac{I’}{I_k}=frac{varepsilon}{2r}cdot frac{r}{varepsilon}=frac{1}{2}to I’=frac{1}{2}I_kleft(2.7right).]
Используем уравнения (2.1) и (2.2) выразим внутреннее сопротивление источника тока:
[varepsilon=Ileft(R+rright);; I_kr=varepsilon to Ileft(R+rright)=I_krto rleft(I_k+Iright)=IRto r=frac{IR}{I_k-I}left(2.8right).]
Подставим результаты из (2.7) и (2.8) в третью формулу системы (2.6), искомая мощность будет равна:
[P_{p max}={left(frac{1}{2}I_kright)}^2frac{IR}{I_k-I}.]
Ответ. $P_{p max}={left(frac{1}{2}I_kright)}^2frac{IR}{I_k-I}$
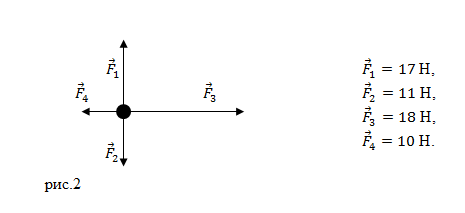
Читать дальше: формула равнодействующей всех сил.
Пишу для школьников (для лучшего понимания ими основ физики). Материал излагаю в соответствии с признанной ныне научной трактовкой физических явлений. Критике существующей теории и глубоким теоретическим рассуждениям здесь не место.
На рисунке изображена замкнутая электрическая цепь, состоящая из источника постоянного тока и переменной нагрузки во внешней части цепи.
Источником постоянного тока может быть электрическая машина, о которой говорится в статье “Искровой разряд”; батарея гальванических элементов, аккумулятор и др.
Роль источника тока заключается в создании (генерировании) электрической энергии: в разделении положительных и отрицательных зарядов; в создании и поддерживании разности потенциалов между конечными точками цепи, в которую включена нагрузка (электрическая лампочка, электроплитка. электродвигатель и т. д.).
При прохождении тока через нагрузку электрическая энергия превращается в другие виды энергии :тепловую (в электроплитке); в тепло и свет (в электрической лампе); в механическую энергию (в электродвигателе).
Превращение энергии из одного вида в другой всегда связано с работой.
При прохождении тока по проводнику совершается работа, её совершают электрические силы (или электрическое поле). Кратко эту работу называют работой тока.
Рассматривая участок цепи, по которому проходит ток, получим следующее выражение для работы тока:
Работа тока равна произведению напряжения между концами участка на протекающий ток и время его протекания.
В случае, если участок цепи однородный (не содержит источника тока), то
тогда получим ещё две формулы для работы тока:
Если ток проходит через неподвижный проводник, то единственным результатом работы тока является его нагревание. Тогда количество выделившейся теплоты
Это запись закона Джоуля – Ленца.
Если кроме нагревания ток совершает ещё механическую работу, например, приводя в действие электродвигатель (мотор), то работа
лишь частично переходит в тепло.
В этом случае работа тока больше количества выделившейся теплоты, но закон Джоуля – Ленца выполняется.
Работа, совершаемая током в единицу времени, называется мощностью тока:
Единицей мощности тока является 1 Вт:
1 Вт – мощность выделяемая током 1 А в проводнике, между концами которого поддерживается напряжение 1 В.
Основная формула мощности для участка цепи:
Мощность постоянного тока на любом участке цепи выражается произведением силы тока на напряжение между концами участка цепи.
Так как для однородного участка цепи
то мощность можно найти ещё по формулам:
Обычно говорят не о работе, а о потребляемой из сети некоторым прибором (электроплитка, лампочки и др.) или двигателем (мотором) мощности электрического тока. Говоря о мощности (например, электродвигателя), отмечают, что работа двигателя совершается за счёт тока.
На приборах часто отмечается потребляемая ими мощность – мощность, необходимая для нормальной работы этого прибора.
Согласно закону сохранения энергии, для замкнутой электрической цепи можно записать:
Здесь
есть полная или затраченная работа, совершаемая сторонними силами, существующими внутри источника, по переносу заряда по цепи.
В гальваническом элементе такими силами являются силы химической реакции.
– это полезная работа, совершаемая электрическим полем при прохождении тока через нагрузку;
это работа, совершаемая внутри источника, по преодолению его внутреннего сопротивления.
Так как работа, совершённая за единицу времени, есть мощность, то из уравнения (1) получим выражение для мощности:
Здесь
есть полная или затраченная мощность, это мощность развиваемая источником тока.
это мощность выделяемая внутри источника тока
это полезная мощность, создаваемая во внешней части цепи (на нагрузке).
Здесь U – напряжение на зажимах источника при замкнутой цепи (при разомкнутой цепи оно равно ЭДС источника).
Так как для однородного участка цепи напряжение равно произведению тока на сопротивление, то полезную мощность можно найти ещё по следующей формуле:
Ток в замкнутой цепи
тогда формулу для полезной мощности можно записать так:
Проанализируем зависимость полезной мощности от сопротивления нагрузки.
При коротком замыкании вся развиваемая источником мощность выделяется на его внутреннем сопротивлении в виде теплоты.
Таким образом, полезная мощность, развиваемая во внешней цепи, достигает максимального значения тогда, когда сопротивление нагрузки равно внутреннему сопротивлению источника.
На следующем рисунке показан график зависимости полезной мощности от сопротивления нагрузки.
Получена формула для нахождения максимальной полезной мощности
При этом ток в цепи в два раза меньше тока короткого замыкания:
Но чему при этом будет равно КПД источника?
Коэффициент полезного действия (КПД) источника показывает, какая часть затраченной (полной) работы источника пошла на пользу или КПД есть отношение полезной работы к затраченной:
Получается, что если добиваться максимальной мощности во внешней цепи, то получим КПД работы всего 50%, то есть половина затраченной мощности источника расходуется бесполезно – переходит в тепло, нагревая источник тока.
Выгоднее брать сопротивление нагрузки больше внутреннего сопротивления источника. Тогда ток в цепи уменьшится, а КПД источника увеличится.
Подумайте над решением следующих задач.
1. ЭДС аккумулятора 2 В, его внутреннее сопротивление 0,4 Ом, сопротивление внешней цепи 1 Ом. Найти разность потенциалов на зажимах аккумулятора и КПД его работы. Ответ: 1,43 В; 71 %.
2. Какую максимальную полезную мощность может выделить аккумулятор с ЭДС 10 В и внутренним сопротивлением 1 Ом? Каково при этом сопротивление внешней цепи? Ответ: 25 Вт; 1 Ом.
3. КПД источника тока, замкнутого на внешнее сопротивление R, равно 60%. Каков будет КПД источника, если внешнее сопротивление увеличить в 6 раз? Ответ: 90%.
Ответ: 7,7 Вт; 12 Вт; 40%; 25%.
Ответ: 2,7 10 4 кг.
К.В. Рулёва
Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Сообщите друзьям о существовании этого канала.
Предыдущая запись: Решение задач на мощность тока.
Следующая запись: Ещё раз о зарядке и разрядке конденсатора.
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
Единицей измерения в Международной системе единиц (СИ) является ватт (русское обозначение: Вт, международное: W).
Мгновенная электрическая мощность[править | править код]
Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки в точку , к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки в точку . Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу или над ним будет совершена работа, численно равная электрическому напряжению, действующему на участке цепи. Умножив напряжение на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца.
Мощность, по определению, — это работа в единицу времени.
Введём обозначения:
— напряжение на участке (принимаем его постоянным на интервале )
— количество зарядов, прошедших от к за время
— работа, совершённая зарядом при движении по участку
— мощность.
Записывая вышеприведённые рассуждения, получаем:
Для единичного заряда на участке :
Для всех зарядов:
Поскольку ток есть электрический заряд, протекающий по проводнику в единицу времени, то есть по определению, в результате получаем:
Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:
Если участок цепи содержит резистор c электрическим сопротивлением , то:
Дифференциальные выражения для электрической мощности[править | править код]
Мощность, выделяемая в единице объёма, равна:
где — напряжённость электрического поля,
— плотность тока.
Отрицательное значение скалярного произведения (векторы и противонаправлены или образуют тупой угол) означает, что в данной точке электрическая мощность не рассеивается, а генерируется за счёт работы сторонних сил.
В случае изотропной среды в линейном приближении:
где — удельная проводимость, величина, обратная удельному сопротивлению.
В случае наличия анизотропии (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла) в линейном приближении:
где — тензор проводимости.
Мощность постоянного тока[править | править код]
Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:
.
Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:
где — электрическое сопротивление.
Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:
где — ЭДС.
Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность прибавляется к поглощаемой или вычитается из отдаваемой.
Мощность переменного тока[править | править код]
В цепях переменного тока формула для мощности постоянного тока может быть применена лишь для расчёта мгновенной мощности, которая сильно изменяется во времени и для большинства простых практических расчётов не слишком полезна непосредственно. Прямой расчёт среднего значения мощности требует интегрирования по времени. Для вычисления мощности в цепях, где напряжение и ток изменяются периодически, среднюю мощность можно вычислить, интегрируя мгновенную мощность в течение периода. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.
Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.
Активная мощность[править | править код]
Единица измерения в СИ — ватт[1].
.
Среднее за период значение мгновенной мощности называется активной электрической мощностью или электрической мощностью:
.
В цепях однофазного синусоидального тока , где и — среднеквадратичные значения напряжения и тока, — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи или её проводимость по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью активная связана соотношением .
В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отражённой мощностью.
Реактивная мощность[править | править код]
Единица измерения, по предложению Международной электротехнической комиссии, – вар (вольт-ампер реактивный); (русское обозначение: вар; международное: var). В терминах единиц СИ, как отмечено в 9-ом издании Брошюры СИ, вар когерентен произведению вольт-ампер. В Российской Федерации эта единица допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения в области «электротехника»[1][2]:
.
Вар определяется как реактивная мощность цепи с синусоидальным переменным током при действующих значениях напряжения 1 В и тока 1 А, если сдвиг фазы между током и напряжением [3].
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения и тока , умноженному на синус угла сдвига фаз между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью и активной мощностью соотношением:
Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.
Необходимо отметить, что величина для значений от 0 до плюс 90° является положительной величиной. Величина для значений от 0 до −90° является отрицательной величиной. В соответствии с формулой , реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.
Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.
Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии, возвращаемой от индуктивной и ёмкостной нагрузки в источник переменного напряжения.
Полная мощность[править | править код]
Единица измерения в СИ — ватт. Кроме того, используется внесистемная единица вольт-ампер (русское обозначение: В·А; международное: V·A). В Российской Федерации эта единица допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения «электротехника»[1][2].
Полная мощность — величина, равная произведению действующих значений периодического электрического тока в цепи и напряжения на её зажимах связана с активной и реактивной мощностями соотношением:
где — активная мощность,
— реактивная мощность (при индуктивной нагрузке , а при ёмкостной ).
Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:
Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому полная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.
Комплексная мощность[править | править код]
Мощность, аналогично импедансу, можно записать в комплексном виде:
где — комплексное напряжение,
— комплексный ток,
— импеданс,
— оператор комплексного сопряжения.
Модуль комплексной мощности равен полной мощности Действительная часть равна активной мощности а мнимая — реактивной мощности с корректным знаком в зависимости от характера нагрузки.
Измерения[править | править код]
- Для измерения электрической мощности применяются ваттметры и варметры, можно также использовать косвенный метод, с помощью вольтметра, амперметра и фазометра.
- Для измерения коэффициента реактивной мощности применяют фазометры
- Государственный эталон мощности — ГЭТ 153—2012 Государственный первичный эталон единицы электрической мощности в диапазоне частот от 1 до 2500 Гц. Институт-хранитель: ВНИИМ
Потребление мощности некоторыми электроприборами[править | править код]
| Электрический прибор | Мощность,Вт |
|---|---|
| Лампочка фонарика | 1 |
| Сетевой роутер, хаб | 10…20 |
| Системный блок ПК | 100…1700 |
| Системный блок сервера | 200…1500 |
| Монитор для ПК ЭЛТ | 15…200 |
| Монитор для ПК ЖК | 2…40 |
| Лампа люминесцентная бытовая | 5…30 |
| Лампа накаливания бытовая | 25…150 |
| Холодильник бытовой | 15…700 |
| Электропылесос | 100… 3000 |
| Электрический утюг | 300…2 000 |
| Стиральная машина | 350…2 000 |
| Электрическая плитка | 1000…2000 |
| Сварочный аппарат бытовой | 1000…5500 |
| Двигатель лифта невысокого дома | 3 000…15 000 |
| Двигатель трамвая | 45 000…75 000 |
| Двигатель электровоза | 650 000 |
| Электродвигатель шахтной подъёмной машины | 1 000 000…5 000 000 |
| Электродвигатель прокатного стана | 6 000 000…32 000 000 |
Выходная мощность[править | править код]
Измеряется как долговременная (RMS), так и кратковременная (PMO, PMPO) мощности, способные отдавать усилителями мощности.
также см.: КПД
См. также[править | править код]
- Ваттметр
- Электрический ток
- Коэффициент мощности
- Список параметров напряжения и силы электрического тока
- Закон Ома
- КПД
Примечания[править | править код]
Литература[править | править код]
- ГОСТ 8.417-2002 Единицы величин.
- ПР 50.2.102-2009 Положение о единицах величин, допускаемых к применению в Российской Федерации.
- Бессонов Л. А. Теоретические основы электротехники. — М.: Высшая школа, 1984.
- Гольдштейн Е. И., Сулайманов А. О., Гурин Т. С. Мощностные характеристики электрических цепей при несинусоидальных токах и напряжениях. ТПУ, — Томск, 2009, Деп. в ВИНИТИ, 06.04.09, № 193 — 2009. — 146 с.
Ссылки[править | править код]
- Преобразование энергии в электрической цепи
- Для чего нужна компенсация реактивной мощности
- Расчет мощности по току и напряжению // asutpp.ru