Полезная мощность на валу двигателя постоянного двигателя
На чтение 8 мин. Обновлено 20 ноября, 2020
Электродвигатель постоянного тока
Основные параметры электродвигателя постоянного тока
Постоянная момента
,
- где M — момент электродвигателя, Нм,
- – постоянная момента, Н∙м/А,
- I — сила тока, А
Постоянная ЭДС
Направление ЭДС определяется по правилу правой руки. Направление наводимой ЭДС противоположно направлению протекающего в проводнике тока.
Наведенная ЭДС последовательно изменяется по направлению из-за перемещения проводников в магнитном поле. Суммарная ЭДС, равная сумме ЭДС в каждой катушке, прикладывается к внешним выводам двигателя. Это и есть противо-ЭДС. Направление противо-ЭДС противоположно приложенному к двигателю напряжению. Значение противо-ЭДС пропорционально частоте вращения и определяется из следующего выражения: [1]
,
Постоянные момента и ЭДС в точности равны между собой KT = KE. Постоянные KT и KE равны друг другу, если они определены в единой системе едениц.
Постоянная электродвигателя
Одним из основных параметров электродвигателя постоянного тока является постоянная электродвигателя Kм. Постоянная электродвигателя определяет способность электродвигателя преобразовывать электрическую энергию в механическую.
,
Постоянная электродвигателя не зависит от соединения обмоток, при условии, что используется один и тот же материал проводника. Например, обмотка двигателя с 6 ветками и 2 параллельными проводами вместо 12 одиночных проводов удвоят постоянную ЭДС, при этом постоянная электродвигателя останется не изменой.
Жесткость механической характеристики двигателя
,
- где — жесткость механической характеристики электродвигателя постоянного тока
Напряжение электродвигателя
Уравнение баланса напряжений на зажимах двигателя постоянного тока имеет вид (в случае коллекторного двигателя не учитывается падение напряжения в щеточно-коллекторном узле):
,
Уравнение напряжения выраженное через момент двигателя будет выглядеть следующим образом:
Соотношение между моментом и частотой вращения при двух различных напряжениях питания двигателя постоянного тока неизменно. При увеличении частоты вращения момент линейно уменьшается. Наклон этой функции KTKE/R постоянный и не зависит от значения напряжения питания и частоты вращения двигателя.
Благодаря таким характеристикам упрощается управление частотой вращения и углом поворота двигателей постоянного тока. Это характерно для коллекторных и вентильных двигателей постоянного тока, что нельзя сказать о двигателях переменного тока и шаговых двигателях [1].
Мощность электродвигателя постоянного тока
Упрощенная модель электродвигателя выглядит следующим образом:
- где I – сила тока, А
- U — напряжение, В,
- M — момент электродвигателя, Н∙м
- R — сопротивление токопроводящих элементов, Ом,
- L — индуктивность, Гн,
- Pэл — электрическая мощность (подведенная), Вт
- Pмех — механическая мощность (полезная), Вт
- Pтеп — тепловые потери, Вт
- Pинд — мощность затрачиваемая на заряд катушки индуктивности, Вт
- Pтр — потери на трение, Вт
Механическая постоянная времени
Механическая постоянная времени — это время, отсчитываемое с момента подачи постоянного напряжения на электродвигатель, за которое частота вращения ненагруженного электродвигателя достигает уровня в 63,21% (1-1/e) от своего конечного значения.
,
- где — механическая постоянная времени, с
Источник
§5.6. Двигатели постоянного тока. Основные характеристики
Двигатели независимого и параллельного возбуждения.
Схема включения двигателя независимого возбуждения показана на рис. 5.19.
Рис. 5.19.
В цепь якоря может быть включено добавочное сопротивление Rд, например пусковой реостат. Для регулирования тока возбуждения в цепь обмотки возбуждения может быть включен регулировочный реостат Rр. У двигателя параллельного возбуждения обмотки якоря и возбуждения подключены к одному источнику питания, и напряжение на них одинаковое. Следовательно, двигатель параллельного возбуждения можно рассматривать как двигатель независимого возбуждения при Uя= Uв.
Механические характеристики.
Механические характеристики двигателей принято подразделять на естественные и искусственные. Естественная характеристика соответствует номинальному напряжению питания и отсутствию добавочных сопротивлений в цепях обмоток двигателя. Если хотя бы одно из перечисленных условий не выполняется, характеристика называется искусственной.
Уравнения электромеханической ω=f(I я) и механической ω=f(M эм.) характеристик могут быть найдены из уравнения равновесия ЭДС и напряжений для якорной цепи двигателя, записанного на основании второго закона Кирхгофа:
где R я – активное сопротивление якоря.
Преобразуя (5.35) с учетом (5.6), получим уравнение электромеханической характеристики
В соответствии с (5.10) ток якоря I я=M эм./kФ и выражение (5.36) преобразуется в уравнение механической характеристики:
Это уравнение можно представить в виде ω= ω о.ид.— Δ ω, где
ω о.ид — угловая скорость идеального холостого хода ( при Iя=0 и, соответственно, Мэм.=0 ); Δ ω= Мэм. [(Rя+Rд)/(kФ) 2 ]– уменьшение угловой скорости, обусловленное нагрузкой на валу двигателя и пропорциональное сопротивлению якорной цепи.
Семейство механических характеристик при номинальном напряжении на якоре и потоке возбуждения и различных добавочных сопротивлениях в цепи якоря изображено на рис. 5.20,а.
Рис.5.20
Механические характеристики двигателей принято оценивать по трем показателям: устойчивости, жесткости и линейности.
Естественная механическая характеристика, соответствующая (5.37) при Rд=0, изображена прямой линией 1. Механическая характеристика линейная; отклонение от линейного закона может быть вызвано реакцией якоря, приводящей к изменению потока Ф. Эта характеристика жесткая, так как при изменении момента нагрузки и соответственно скорости поток возбуждения не изменяется. Жесткость характеристики уменьшается при введении добавочного сопротивления в цепь якоря (прямые линии 2 и 3 – искусственные реостатные характеристики). Характеристики устойчивые, так как dω/dMэм. Мст. Если это условие выполняется, то при включении двигателя в сеть ротор приходит в движение и разгоняется до установившегося режима. Ввиду того, что ротор обладает моментом инерции, разгоняется он не мгновенно – нарастание скорости происходит по закону, близкому к экспоненте.
Пуск двигателя постоянного тока осложняется тем, что при ω=0 ЭДС Eя=0 и пусковой ток якоря Iяп= Uя/ Rя может в 10 – 20 раз превышать номинальный ток, что опасно как для двигателя (усиление искрения, динамические перегрузки), так и для источника питания. Поэтому важнейшими показателями пускового режима являются кратность пускового тока Kiп= Iп/ Iном и кратность пускового момента Кмп= Мп/ Мном. При пуске необходимо обеспечить требуемую кратность пускового момента при возможно меньшей кратности пускового тока.
Прямой пуск применяют обычно при кратности пускового тока K iп?6. При большем значении Kiп применяют способы пуска, обеспечивающие снижение тока Iяп либо за счет подачи пониженного напряжения на обмотку якоря, либо за счет введения добавочного сопротивления в цепь якоря. Первый способ применяется в основном при работе двигателей в системах автоматического регулирования с якорным способом управления. Второй способ, называемый реостатным, распространен наиболее широко в нерегулируемом приводе. Сопротивление пускового реостата Rп= Rд (см. рис. 5.19) выбирают таким, чтобы ограничить Iяп до (1,4 – 1,8) Iя.ном у двигателей средней мощности и до (2,0 – 2,5) Iя.ном у двигателей малой мощности. По мере разгона якоря ток якоря уменьшается и пусковой реостат постепенно выводится.
Реверсирование.
Реверсирование двигателя осуществляется либо изменением полярности напряжения на обмотке якоря, либо на обмотке возбуждения. В обоих случаях изменяется знак электромагнитного момента двигателя Мэм и соответственно направление вращения ротора.
Торможение.
У двигателей независимого и параллельного возбуждения возможны три тормозных режима: рекуперативное торможение, торможение противовключением и динамическое. При анализе тормозных режимов необходимо строить механические характеристики машины во всех четырех квадрантах плоскости Мэм, ω. Для построения механических характеристик можно пользоваться одним и тем же уравнением (5.37) с учетом знака Мэм в различных режимах работы машины.
Рекуперативное торможение, или генераторное торможение с отдачей энергии в сеть, может быть осуществлено при ω>ω о.ид. В этом случае ЭДС якоря Eя > Uя (см. (5.6) и (5.38)), ток якоря меняет направление, машина переходит в генераторный режим и электромагнитный момент становится тормозным. Механической характеристикой в режиме рекуперативного торможения является продолжение механической характеристики двигателя во II квадранте (ω>0, Mэм 2 . Механические характеристики тормозного режима расположены во II квадранте плоскости Мэм,ω (рис. 5.22, б, Rд2>Rд3).
В момент переключения двигатель переходит из точки А естественной характеристики двигательного режима 1 в точку В характеристики тормозного режима 2, момент Мэм меняет знак и начинается динамическое торможение. Угловая скорость уменьшается, но при этом довольно резко уменьшается и тормозной момент (переход из точки В в С). С целью увеличения тормозного момента производится уменьшение добавочного сопротивления Rд (переход из точки С в точку D). Торможение происходит до нулевой скорости.
Двигатели последовательного и смешанного возбуждения.
У двигателя последовательного возбуждения (рис. 5.23,а) ток якоря протекает по обмотке возбуждения (Iв= Iя) и это определенным образом сказывается на основных характеристиках двигателя. При отсутствии насыщения магнитопровода можно принять, что
где Kф – коэффициент пропорциональности.
С учетом (5.40) уравнения (5.10) и (5.37) принимают вид
где Rв – сопротивление обмотки возбуждения.
Механическая характеристика (рис. 5.23, б пунктирная линия) мягкая, имеет гиперболическую форму и обеспечивает устойчивую работу двигателя. Мягкость характеристики объясняется тем, что с увеличением момента нагрузки и соответственно уменьшением скорости растут ток и поток возбуждения. При больших нагрузках начинает сказываться насыщение магнитопровода и характеристика отличается от расчетной (сплошная линия). Двигатель последовательного возбуждения нельзя пускать без нагрузки на валу, так как при Мэм → 0, угловая скорость ω → ∞.
Квадратичная зависимость момента от тока позволяет при одинаковой кратности пускового тока получать у двигателя последовательного возбуждения больший пусковой момент, чем у двигателя независимого или параллельного возбуждения.
Пуск, реверсирование, торможение и регулирование угловой скорости двигателей последовательного возбуждения осуществляется теми же способами, что и у двигателей независимого и параллельного возбуждения с учетом специфики включения обмоток.
Рис.5.23
Двигатели смешанного возбуждения по своим характеристикам занимают промежуточное положение между двигателями независимого и последовательного возбуждения. Конкретный вид характеристик зависит от того, согласно или встречно(по потоку) включены между собой обмотки возбуждения.
Источник
Источник
Мощность и вращающий момент электродвигателя
Данная глава посвящена вращающему моменту: что это такое, для чего он нужен и др. Мы также разберём типы нагрузок в зависимости от моделей насосов и соответствие между электродвигателем и нагрузкой насоса.
Вы когда-нибудь пробовали провернуть вал пустого насоса руками? Теперь представьте, что вы поворачиваете его, когда насос заполнен водой. Вы почувствуете, что в этом случае, чтобы создать вращающий момент, требуется гораздо большее усилие.
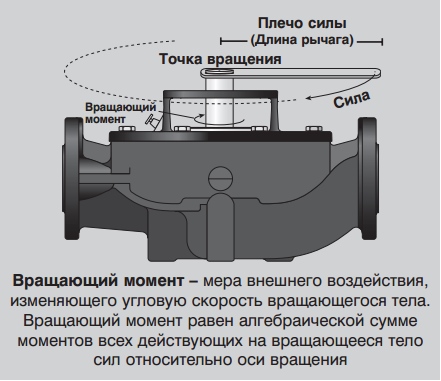
А теперь представьте, что вам надо крутить вал насоса несколько часов подряд. Вы бы устали быстрее, если бы насос был заполнен водой, и почувствовали бы, что потратили намного больше сил за тот же период времени, чем при выполнении тех же манипуляций с пустым насосом. Ваши наблюдения абсолютно верны: требуется большая мощность, которая является мерой работы (потраченной энергии) в единицу времени. Как правило, мощность стандартного электродвигателя выражается в кВт.
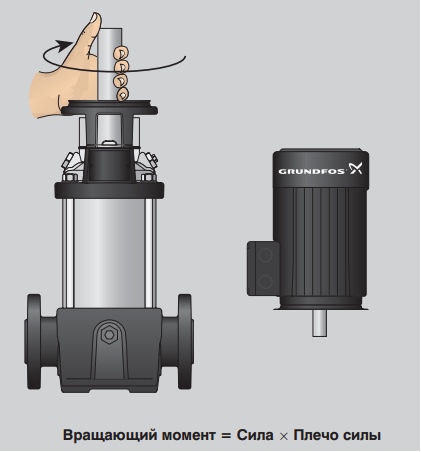
Вращающий момент (T) – это произведение силы на плечо силы. В Европе он измеряется в Ньютонах на метр (Нм).
Как видно из формулы, вращающий момент увеличивается, если возрастает сила или плечо силы – или и то и другое. Например, если мы приложим к валу силу в 10 Н, эквивалентную 1 кг, при длине рычага (плече силы) 1 м, в результате, вращающий момент будет 10 Нм. При увеличении силы до 20 Н или 2 кг, вращающий момент будет 20 Нм. Таким же образом, вращающий момент был бы 20 Нм, если бы рычаг увеличился до 2 м, а сила составляла 10 Н. Или при вращающем моменте в 10 Нм с плечом силы 0,5 м сила должна быть 20 Н.
Работа и мощность
Теперь остановимся на таком понятии как «работа», которое в данном контексте имеет особое значение. Работа совершается всякий раз, когда сила – любая сила – вызывает движение. Работа равна силе, умноженной на расстояние. Для линейного движения мощность выражается как работа в определённый момент времени.
Если мы говорим о вращении, мощность выражается как вращающий момент (T), умноженный на частоту вращения (w).
Частота вращения объекта определяется измерением времени, за которое определённая точка вращающегося объекта совершит полный оборот. Обычно эта величина выражается в оборотах в минуту, т.е. мин-1 или об/мин. Например, если объект совершает 10 полных оборотов в минуту, это означает, что его частота вращения: 10 мин-1 или 10 об/мин.
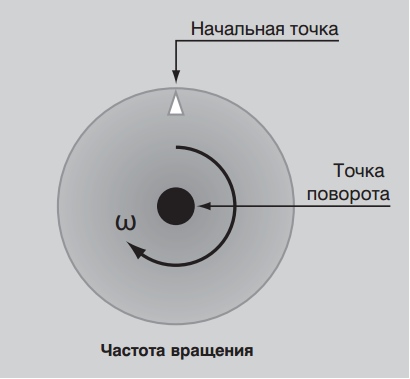
Итак, частота вращения измеряется в оборотах в минуту, т.е. мин-1.
Приведем единицы измерения к общему виду.
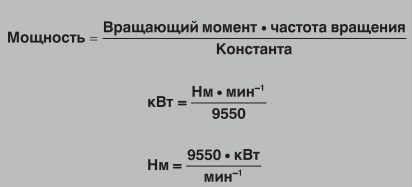
Для наглядности возьмём разные электродвигатели, чтобы более подробно проанализировать соотношение между мощностью, вращающим моментом и частотой вращения. Несмотря на то, что вращающий момент и частота вращения электродвигателей сильно различаются, они могут иметь одинаковую мощность.
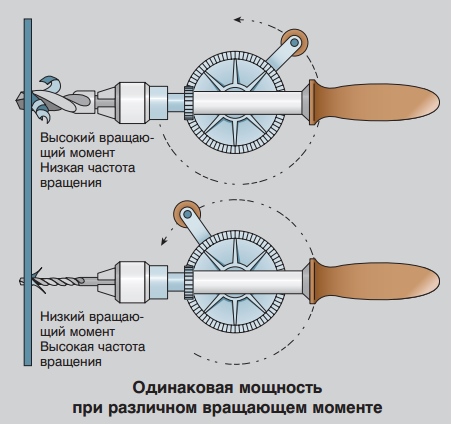
Например, предположим, что у нас 2-полюсный электродвигатель (с частотой вращения 3000 мин-1) и 4-полюсной электродвигатель (с частотой вращения 1500 мин-1). Мощность обоих электродвигателей 3,0 кВт, но их вращающие моменты отличаются.
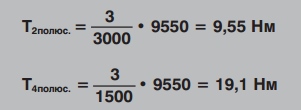
Таким образом, вращающий момент 4-полюсного электродвигателя в два раза больше вращающего момента двухполюсного электродвигателя с той же мощностью.
Как образуется вращающий момент и частота вращения?
Теперь, после того, как мы изучили основы вращающего момента и скорости вращения, следует остановиться на том, как они создаются.
В электродвигателях переменного тока вращающий момент и частота вращения создаются в результате взаимодействия между ротором и вращающимся магнитным полем. Магнитное поле вокруг обмоток ротора будет стремиться к магнитному полю статора. В реальных рабочих условиях частота вращения ротора всегда отстаёт от магнитного поля. Таким образом, магнитное поле ротора пересекает магнитное поле статора и отстает от него и создаёт вращающий момент. Разницу в частоте вращения ротора и статора, которая измеряется в %, называют скоростью скольжения.
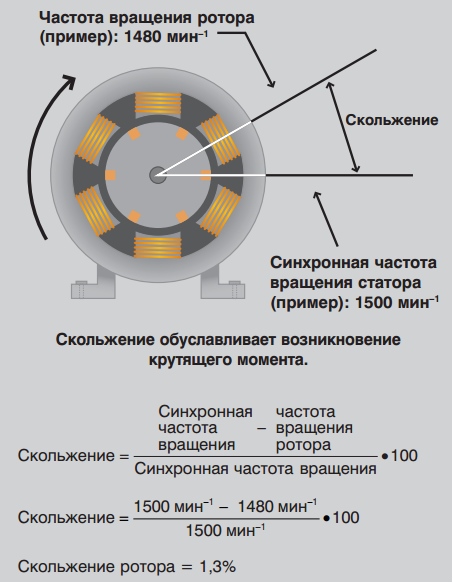
Скольжение является основным параметром электродвигателя, характеризующий его режим работы и нагрузку. Чем больше нагрузка, с которой должен работать электродвигатель, тем больше скольжение.
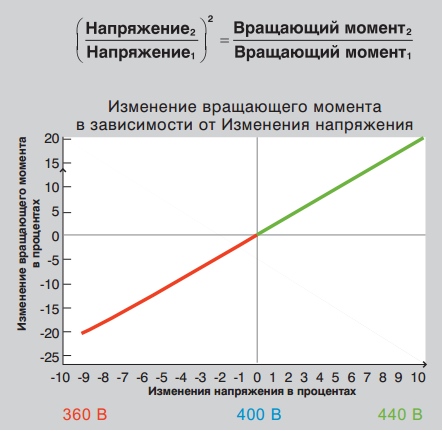
Помня о том, что было сказано выше, разберём ещё несколько формул. Вращающий момент индукционного электродвигателя зависит от силы магнитных полей ротора и статора, а также от фазового соотношения между этими полями. Это соотношение показано в следующей формуле:
Сила магнитного поля, в первую очередь, зависит от конструкции статора и материалов, из которых статор изготовлен. Однако напряжение и частота тока также играют важную роль. Отношение вращающих моментов пропорционально квадрату отношения напряжений, т.е. если подаваемое напряжение падает на 2%, вращающий момент, следовательно, уменьшается на 4%.
Потребляемая мощность электродвигателя
Ток ротора индуцируется через источник питания, к которому подсоединён электродвигатель, а магнитное поле частично создаётся напряжением. Входную мощность можно вычислить, если нам известны данные источника питания электродвигателя, т.е. напряжение, коэффициент мощности, потребляемый ток и КПД.

В Европе мощность на валу обычно измеряется в киловаттах. В США мощность на валу измеряется в лошадиных силах (л.с.).
Если вам необходимо перевести лошадиные силы в киловатты, просто умножьте соответствующую величину (в лошадиных силах) на 0,746. Например, 20 л.с. равняется (20 • 0,746) = 14,92 кВт.
И наоборот, киловатты можно перевести в лошадиные силы умножением величины в киловаттах на 1,341. Это значит, что 15 кВт равняется 20,11 л.с.
Момент электродвигателя
Мощность [кВт или л.с.] связывает вращающий момент с частотой вращения, чтобы определить общий объём работы, который должен быть выполнен за определённый промежуток времени.
Рассмотрим взаимодействие между вращающим моментом, мощностью и частотой вращения, а также их связь с электрическим напряжением на примере электродвигателей Grundfos. Электродвигатели имеют одну и ту же номинальную мощность как при 50 Гц, так и при 60 Гц.

Это влечёт за собой резкое снижение вращающего момента при 60 Гц: частота 60 Гц вызывает 20%-ное увеличение числа оборотов, что приводит к 20%-ному уменьшению вращающего момента. Большинство производителей предпочитают указывать мощность электродвигателя при 60 Гц, таким образом, при снижении частоты тока в сети до 50 Гц электродвигатели будут обеспечивать меньшую мощность на валу и вращающий момент. Электродвигатели обеспечивают одинаковую мощность при 50 и 60 Гц.
Графическое представление вращающего момента электродвигателя изображено на рисунке.
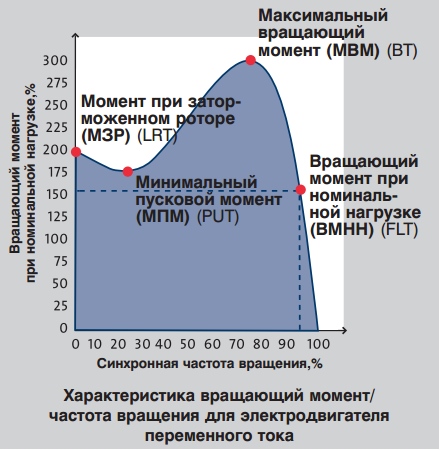
Иллюстрация представляет типичную характеристику вращающий момент/частота вращения. Ниже приведены термины, используемые для характеристики вращающего момента электродвигателя переменного тока.
Пусковой момент (Мп): Механический вращающий момент, развиваемый электродвигателем на валу при пуске, т.е. когда через электродвигатель пропускается ток при полном напряжении, при этом вал застопорен.
Минимальный пусковой момент (Ммин): Этот термин используется для обозначения самой низкой точки на кривой вращающий момент/частота вращения электродвигателя, нагрузка которого увеличивается до полной скорости вращения. Для большинства электродвигателей Grundfos величина минимального пускового момента отдельно не указывается, так как самая низкая точка находится в точке заторможенного ротора. В результате для большинства электродвигателей Grundfos минимальный пусковой момент такой же, как пусковой момент.
Блокировочный момент (Мблок): Максимальный вращающий момент – момент, который создаёт электродвигатель переменного тока с номинальным напряжением, подаваемым при номинальной частоте, без резких скачков скорости вращения. Его называют предельным перегрузочным моментом или максимальным вращающим моментом.
Вращающий момент при полной нагрузке (Мп.н.): Вращающий момент, необходимый для создания номинальной мощности при полной нагрузке.
Нагрузка насосов и типы нагрузки электродвигателя
Выделяют следующие типы нагрузок:
Постоянная мощность
Термин «постоянная мощность» используется для определённых типов нагрузки, в которых требуется меньший вращающий момент при увеличении скорости вращения, и наоборот. Нагрузки при постоянной мощности обычно применяются в металлообработке, например, сверлении, прокатке и т.п.
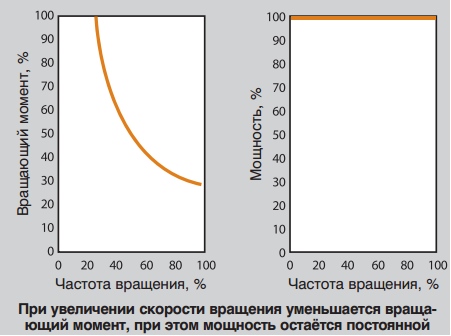
Постоянный вращающий момент
Как видно из названия – «постоянный вращающий момент» – подразумевается, что величина вращающего момента, необходимого для приведения в действие какого- либо механизма, постоянна, независимо от скорости вращения. Примером такого режима работы могут служить конвейеры.
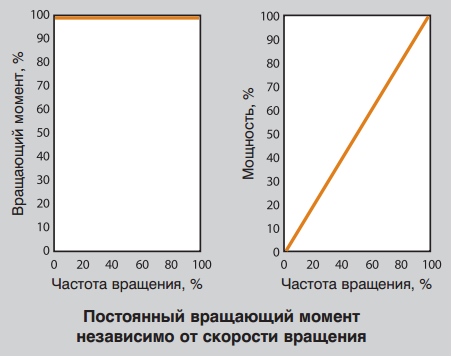
Переменный вращающий момент и мощность
«Переменный вращающий момент» – эта категория представляет для нас наибольший интерес. Этот момент имеет отношение к нагрузкам, для которых требуется низкий вращающий момент при низкой частоте вращения, а при увеличении скорости вращения требуется более высокий вращающий момент. Типичным примером являются центробежные насосы.
Вся остальная часть данного раздела будет посвящена исключительно переменному вращающему моменту и мощности.
Определив, что для центробежных насосов типичным является переменный вращающий момент, мы должны проанализировать и оценить некоторые характеристики центробежного насоса. Использование приводов с переменной частотой вращения обусловлено особыми законами физики. В данном случае это законы подобия, которые описывают соотношение между разностями давления и расходами.
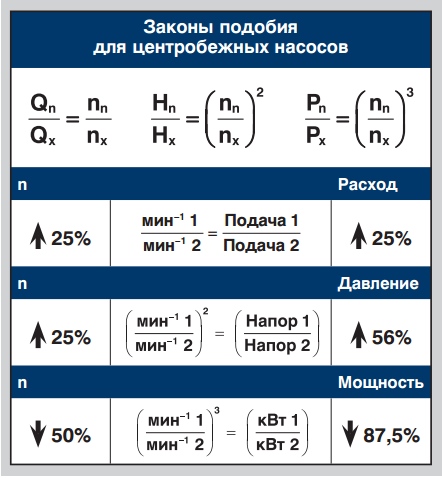
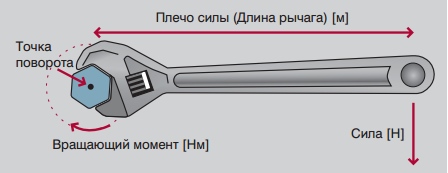
Во-первых, подача насоса прямо пропорциональна частоте вращения. Это означает, что если насос будет работать с частотой вращения на 25% больше, подача увеличится на 25%.
Во-вторых, напор насоса будет меняться пропорционально квадрату изменения скорости вращения. Если частота вращения увеличивается на 25%, напор возрастает на 56%.
В-третьих, что особенно интересно, мощность пропорциональна кубу изменения скорости вращения. Это означает, что если требуемая частота вращения уменьшается на 50%, это равняется 87,5%-ному уменьшению потребляемой мощности.
Итак, законы подобия объясняют, почему использование приводов с переменной частотой вращения более целесообразно в тех областях применения, где требуются переменные значения расхода и давления. Grundfos предлагает ряд электродвигателей со встроенным частотным преобразователем, который регулирует частоту вращения для достижения именно этой цели.
Так же как подача, давление и мощность, потребная величина вращающего момента зависит от скорости вращения.
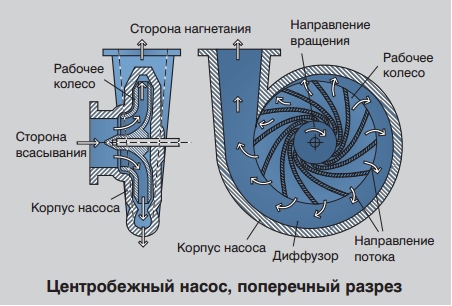
На рисунке показан центробежный насос в разрезе. Требования к вращающему моменту для такого типа нагрузки почти противоположны требованиям при «постоянной мощности». Для нагрузок при переменном вращающем моменте потребный вращающий момент при низкой частоте вращения – мал, а потребный вращающий момент при высокой частоте вращения – велик. В математическом выражении вращающий момент пропорционален квадрату скорости вращения, а мощность – кубу скорости вращения.

Это можно проиллюстрировать на примере характеристики вращающий момент/частота вращения, которую мы использовали ранее, когда рассказывали о вращающем моменте электродвигателя:
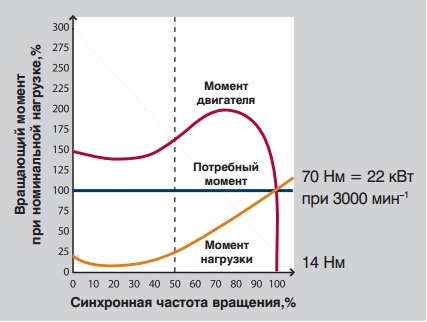
Когда электродвигатель набирает скорость от нуля до номинальной скорости, вращающий момент может значительно меняться. Величина вращающего момента, необходимая при определённой нагрузке, также изменяется с частотой вращения. Чтобы электродвигатель подходил для определённой нагрузки, необходимо чтобы величина вращающего момента электродвигателя всегда превышала вращающий момент, необходимый для данной нагрузки.
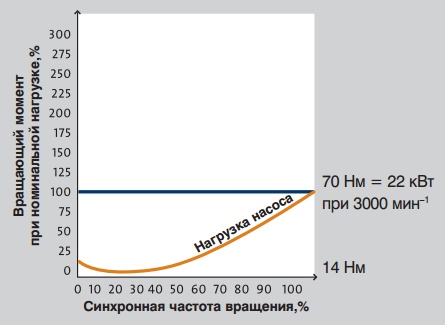
В примере, центробежный насос при номинальной нагрузке имеет вращающий момент, равный 70 Нм, что соответствует 22 кВт при номинальной частоте вращения 3000 мин-1. В данном случае насосу при пуске требуется 20% вращающего момента при номинальной нагрузке, т.е. приблизительно 14 Нм. После пуска вращающий момент немного падает, а затем, по мере того, как насос набирает скорость, увеличивается до величины полной нагрузки.
Очевидно, что нам необходим насос, который будет обеспечивать требуемые значения расход/напор (Q/H). Это значит, что нельзя допускать остановок электродвигателя, кроме того, электродвигатель должен постоянно ускоряться до тех пор, пока не достигнет номинальной скорости. Следовательно, необходимо, чтобы характеристика вращающего момента совпадала или превышала характеристику нагрузки на всём диапазоне от 0% до 100% скорости вращения. Любой «избыточный» момент, т.е. разница между кривой нагрузки и кривой электродвигателя, используется как ускорение вращения.
Соответствие электродвигателя нагрузке
Если нужно определить, отвечает ли вращающий момент определённого электродвигателя требованиям нагрузки, Вы можете сравнить характеристики скорости вращения/вращающего момента электродвигателя с характеристикой скорости вращения/ вращающего момента нагрузки. Вращающий момент, создаваемый электродвигателем, должен превышать потребный для нагрузки вращающий момент, включая периоды ускорения и полной скорости вращения.
Характеристика зависимости вращающего момента от скорости вращения стандартного электродвигателя и центробежного насоса.
Если мы посмотрим на характеристику , то увидим, что при ускорении электродвигателя его пуск производится при токе, соответствующем 550% тока полной нагрузки.
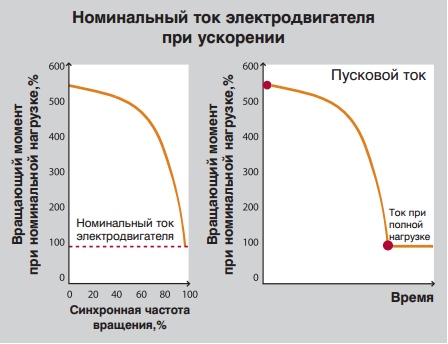
Когда двигатель приближается к своему номинальному значению скорости вращения, ток снижается. Как и следовало ожидать, во время начального периода пуска потери на электродвигателе высоки, поэтому этот период не должен быть продолжительным, чтобы не допустить перегрева.
Очень важно, чтобы максимальная скорость вращения достигалась как можно точнее. Это связано с потребляемой мощностью: например, увеличение скорости вращения на 1% по сравнению со стандартным максимумом приводит к 3%-ному увеличению потребляемой мощности.
Потребляемая мощность пропорциональна диаметру рабочего колеса насоса в четвертой степени.
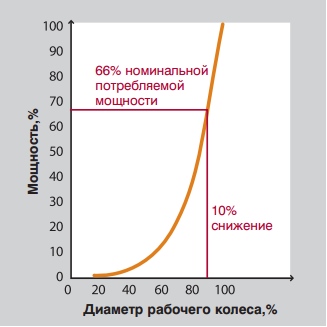
Уменьшение диаметра рабочего колеса насоса на 10% приводит к уменьшению потребляемой мощности на (1- (0.9 * 0.9 * 0.9 * 0.9)) * 100 = 34%, что равно 66% номинальной мощности. Эта зависимость определяется исключительно на практике, так как зависит от типа насоса, конструкции рабочего колеса и от того, насколько вы уменьшаете диаметр рабочего колеса.
Время пуска электрдвигателя
Если нам необходимо подобрать типоразмер электродвигателя для определённой нагрузки, например для центробежных насосов, основная наша задача состоит в том, чтобы обеспечить соответствующий вращающий момент и мощность в номинальной рабочей точке, потому что пусковой момент для центробежных насосов довольно низкий. Время пуска достаточно ограниченно, так как вращающий момент довольно высокий.
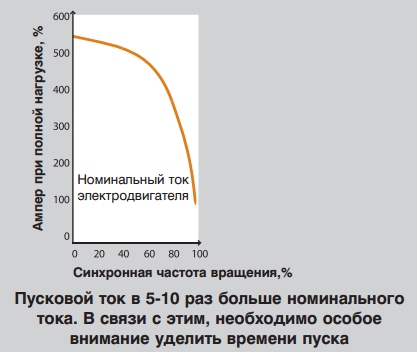
Нередко для сложных систем защиты и контроля электродвигателей требуется некоторое время для их пуска, чтобы они могли замерить пусковой ток электродвигателя. Время пуска электродвигателя и насоса рассчитывается с помощью следующей формулы:
tпуск = время, необходимое электродвигателю насоса, чтобы достичь частоты вращения при полной нагрузке
n = частота вращения электродвигателя при полной нагрузке
Iобщ = инерция, которая требует ускорения, т.е. инерция вала электродвигателя, ротора, вала насоса и рабочих колёс.
Момент инерции для насосов и электродвигателей можно найти в соответствующих технических данных.
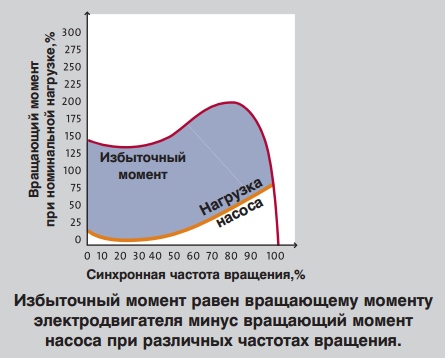
Мизб = избыточный момент, ускоряющий вращение. Избыточный момент равен вращающему моменту электродвигателя минус вращающий момент насоса при различных частотах вращения.
Мизб можно рассчитать по следующим формулам:
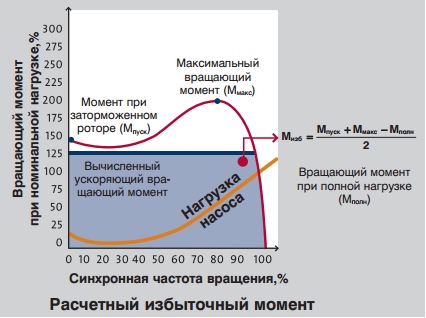

Как видно из приведённых вычислений, выполненных для данного примера с электродвигателем мощностью 4 кВт насоса CR, время пуска составляет 0,11 секунды.
Число пусков электродвигателя в час
Современные сложные системы управления электродвигателями могут контролировать число пусков в час каждого конкретного насоса и электродвигателя. Необходимость контроля этого параметра состоит в том, что каждый раз, когда осуществляется пуск электродвигателя с последующим ускорением, отмечается высокое потребление пускового тока. Пусковой ток нагревает электродвигатель. Если электродвигатель не остывает, продолжительная нагрузка от пускового тока значительно нагревает обмотки статора электродвигателя, что приводит к выходу из строя электродвигателя или сокращению срока службы изоляции.
Обычно за количество пусков, которое может выполнить электродвигатель в час, отвечает поставщик электродвигателя. Например, Grundfos указывает максимальное число пусков в час в технических данных на насос, так как максимальное количество пусков зависит от момента инерции насоса.
Мощность и КПД (eta) электродвигателя
Существует прямая связь между мощностью, потребляемой электродвигателем от сети, мощностью на валу электродвигателя и гидравлической мощностью, развиваемой насосом.
При производстве насосов используются следующие обозначения этих трёх различных типов мощности.
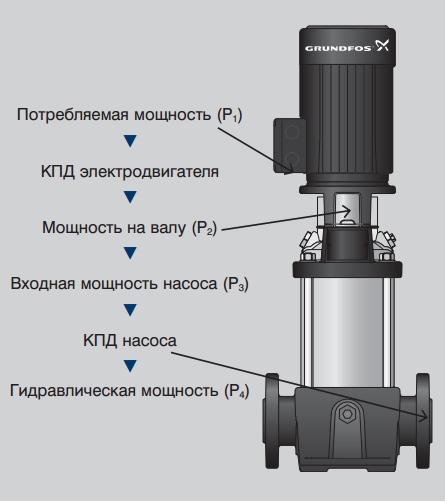
P1 (кВт) Входная электрическая мощность насосов – это мощность, которую электродвигатель насоса получает от источника электрического питания. Мощность P! равна мощности P2, разделённой на КПД электродвигателя.
P2 (кВт) Мощность на валу электродвигателя – это мощность, которую электродвигатель передает на вал насоса.
Р3 (кВт) Входная мощность насоса = P2, при условии, что соединительная муфта между валами насоса и электродвигателя не рассеивает энергию.
Р4 (кВт) Гидравлическая мощность насоса.
Источник
