Моделирование и подсчет запасов полезных ископаемых
Главное преимущество современных методов компьютерного моделирование по сравнению с традиционными методами ручного подсчёта запасов состоит в том, что они позволяют количественно оценить пространственную изменчивость границ рудных тел и содержаний в них металлов. При создании модели минеральных ресурсов и запасов месторождения геолог имеет дело с вероятностной информацией так как располагает относительно редкими фактическими данными качественной характеристики руды в точках опробования разведочных выработок, а пространство между точками опробования является предметом прогнозирования и неопределенности. Задача создания простой и понятной технологии блочного моделирования позволяющей воспроизводить исходные фактические статистические параметры (среднее, дисперсию, разброс значений) содержаний и достигать совпадения с реальными значениями в точках опробования является весьма актуальной, которая благодаря технологии последовательного индикаторного моделирования достаточно оперативно и точно решается без надуманных сложностей геостатистики и математических формул, а за счет здравого геологического смысла. Данной тематике будут посвящены отдельные исследования с целью предложить альтернативные подходы и решения создания моделей методами последовательного индикаторного моделирования.
В настоящей статье, «здесь и сейчас», предлагается рассмотреть проблемы геометрического моделирования как совокупности операций и процедур, для формирования геометризованных запасов месторождения, а также излагаются некоторые соображения, возникшие в суровой реальности недропользования в России вызванной следующими основными факторами и особенностями отечественной методики оценки запасов месторождений.
1. Согласно требованиям ГКЗ, компьютерное моделирование может применяться при подсчете запасов, но только при условии, что подсчет запасов методами блочного моделирования заверяется данными традиционного геометрического подсчета, который опирается на результаты выделения рудных интервалов с учетом бортового содержания в пробе по данным геологической документации и опробования. При использовании метода геометризации запасов по результатам выделения рудных интервалов обычно создаются контуры рудных тел, затем по ним геометризуются запасы для каждого варианта бортового содержания и в пределах этого пространства оценивается средневзвешенное на мощность проб содержание металла. Такой метод геометризации при необходимости оценки запасов руды по нескольким вариантам бортового содержания является достаточно точным, но очень трудоемким. С точки зрения затрат труда и скорости выполнения подсчета запасов, блочное моделирование имеет значительное преимущество в сравнении с геометрическим, и прежде всего, при повариантных подсчетах. Однако, практика применения методов блочного моделирования показывает, что из-за различия в принципах оценки отмечаются незначительные расхождения с данными подсчета традиционными способами. Соответственно, сходством общих цифр результатов блочного моделирования и данных традиционного ручного счета, а также адекватностью отображения их положения в пространстве и определяют, в конечном итоге, качество выполненной модели. Несомненно, представляемые на экспертизу в ГКЗ модели неудовлетворительного качества, разработанные на устаревших преставлениях о методах моделирования, либо на очевидных ошибках, допущенных в процессе моделирования ограничивают и создают сложности применения блочного моделирования в России и формируют предвзятое отношение к данной методике отдельных экспертов и контролирующих органов. Справедливости ради отметим, что ГКЗ делает определенные шаги и работает над методическими рекомендациями по применению блочного моделирования для подсчета запасов, но до массового рассмотрения кондиций и утверждения запасов по данным блочных моделей еще далеко.
2. Нынешнее состояние недропользования в России можно оценить, как кризисное и находящееся в поиске дальнейшего пути развития. В связи с этим, специалистам-геологам приходится разрабатывать новые методы геометрического моделирования, позволяющие сделать процесс менее трудоемким за счет того, что алгоритмы решений соответствующие требованиям традиционного геометрического подсчета эффективно реализуются в зарубежных горно-геологических системах (DATAMINE, MICROMINE и др.) и отечественных программах (DIGIMINE, MINEFRAME), что позволяет предоставлять материалы ТЭО кондиций и подсчета запасов в соответствии с традиционными требованиями ГКЗ. Зачастую под компьютерным моделированием понимают создание блочной модели и подсчет запасов с ее использованием. Однако компьютерное моделирование не замыкается на блочной модели. По сути, в горно-геологических системах предлагается мощный инструмент, обеспечивающий не только быстрое и точное выполнение всех процедур ручного подсчета, но и, главное, трехмерность построений объемных геологических и подсчетных моделей с широкими возможностями многовариантности выделения рудных интервалов, увязке контуров, не говоря уже о мощных возможностях визуализации в 3D пространстве и возможностях формирования качественных графических материалов, в том числе и отвечающих традиционным требованиям ГКЗ.
В свете обозначенных проблем и отмеченных особенностей прохождения процедуры государственной экспертизы утверждения запасов, автором статьи предлагаются некоторые усовершенствования традиционного геометрического подсчета запасов, благодаря современным технологиям трехмерного моделирования.
Важно понимать, что выполнение геометрического моделирования определяется двумя основными взаимосвязанными составляющими этого процесса – аналитической и геометрической.
В основе аналитической составляющей можно выделить следующие основные функциональные блоки обработки данных опробования определяющие последующие геометрию, объемы и пространственное положение рудных запасов в составе качественно выполненной геологической модели:
1. Автоматический поиск и индикация ошибок ввода данных опробования. При создании базы данных опробования выполняется ряд проверок, предохраняющих базу данных от некорректной информации.
2. Расчет рудных интервалов по заданным кондициям по алгоритму соответствующему методике ГКЗ и представление в традиционном виде таких подсчетных таблиц как «Расчет кондиционных интервалов по выработкам», «Расчёт мощностей, КР и средних содержаний по сечениям», «Подсчёт запасов по блокам».
3. Вычисление горизонтальной и истинной мощности, а также контроль выполненных вычислений графическим способом путем построения горизонтальных стрингов, являющихся эквивалентом горизонтальной мощности рудного сечения и автоматический расчет их длины.
4. Автоматический расчет коэффициента рудоносности по каждому рудному сечению, линии, блоку после построения каркасных моделей.
5. Статистический анализ параметров кондиций для повариантного подсчета запасов. Для выполнения такой задачи при помощи значений “От”, “До” и “Шаг” задается диапазон бортовых содержаний, диапазон минимальных рудных мощностей и диапазон максимально допустимых мощностей безрудных прослоев которые необходимо перебрать в процессе расчетов и выдать в табличной форме результаты расчета по каждому варианту параметров кондиций, которые могут быть наглядно проанализированы, например, с помощью гистограмм (рис. 1 а, б.)
На рис. 1 видно, что для классов мощности 3,0-4,0 м относительная доля суммарного метрограмма, как эквивалента запасов металла, преобладает над аналогичными показателями для других классов мощности и наиболее оптимальным параметром минимальной рудной мощности следует принять значение 4 метра.
В основе геометрической составляющей можно выделить следующие основные функциональные блоки обработки данных которые непосредственно формируют геометрию, объемы и пространственное положение рудных запасов:
1. Вычисление объемов каркасов. Несомненно, возможности компьютерных горно-геологических систем для оценки объемов, обладают громадным преимуществом по сравнению с традиционными методами.
2. Визуализация в 3D пространстве (трехмерная визуализация любых данных с выноской значений, раскраской, штриховкой, графиками, а также просмотр всех данных в плоскости как в плане, так и в разрезе). Полное управление трехмерной средой по всем осям, включая поворот, приближение и перемещение.
3. Полуавтоматический способ построения кровли (висячего бока) и подошвы (лежачего бока) рудных тел по заданным вариантам кондиций реализуемый благодаря методу радиальных базисных функций РБФ условно названный здесь как метод вложенных поверхностей. Радиальные базисные функции представляют собой набор жестких методов интерполяции благодаря чему поверхность, построенная с использованием этих функций, будет проходить через все фактические опорные точки. Кроме того, с помощью метода РБФ можно успешно создавать «предсказанные» точки и поверхности экстраполяции на все заданное пространство модели, расширив область распространения исходных опорных точек. После построения неограниченной поверхности пласта ее можно автоматически ограничить до площади, определенной в файле стрингов по контуру подсчетных запасов. Причем имеется возможность полуавтоматически зафиксировать положение экстрополяционных точек в 3D пространстве таким образом, чтобы оно соответствовало с одной стороны заданному значению минимально допустимой рудной мощности, а с другой стороны – выклинивание рудного тела по простиранию и падению произвести на половину расстояния между разведочными линиями. Общее направление и падение рудного тела при экстраполяции сохраняется автоматически. Интерпретация по разрезам (в скважинах) и плану поверхности (в канавах) увязывается автоматически с тем, чтобы контура по разрезам и планам не противоречили друг другу. Вложенность поверхностей и каркасов вариантов бортовых содержаний сохраняется благодаря тому, что используется одинаковое определения треугольников триангуляции (содержащих записи с идентификаторами для трех точек в каждом треугольнике) для всех вариантов, а координаты точек триангуляции пересчитываются в соответствии с границами интервалов рудных сечений. При необходимости полученные поверхности кровли и подошвы объединяются, образуя общую замкнутую объемную модель (солид).
Применение метода вложенных поверхностей для построения каркасов рудных тел, помимо указанных выше преимуществ над ручным оконтуриванием, делает процесс интерполяции и особенно экстраполяции по настоящему трехмерным, так как РБФ учитывает все точки участвующие в построении, а не только те несколько точек, которые в каждом в конкретном разрезе оконтуриваются классическим способом вручную при создании замкнутых стрингов по разрезам. Следует также учитывать, что для ряда месторождений определенного типа (например, осадочных) построение каркасных моделей рудных тел традиционными замкнутыми стрингами может привести к серьёзным ошибкам как в морфологии рудных тел, так и в значениях полученных объёмов руды.
Несомненным достоинством применения метода вложенных поверхностей отмечаем полноценный учет кондиционных показателей – минимальная мощность рудного тела и максимальная мощность прослоев пустых пород при том, что полноценный учет этих показателей при блочном моделировании практически невозможен.
На начальном этапе освоения, метод вложенных поверхностей может показаться достаточно сложным по сравнению с классическим способом построения каркасов по стрингам оконтуренным вручную. Однако тут возникает вопрос – есть ли необходимость создавать полную вложенную модель месторождения с точностью до каждого входящего в нее мелкого рудного тела? Необходимо понимать, что структура распределение запасов руды по рудным телам, как правило, указывает на то, что наибольшая часть выходного продукта (запасов металла) получается из меньшей части входных ресурсов (количество выделенных рудных тел). Проанализировав опыт выполненных работ и другие источники информации по целому ряду золоторудных месторождений возникает вывод, что основная доля запасов сосредоточена преимущественно в нескольких наиболее крупных телах количеством от 2-х до 5-ти, редко более 10. Поэтому является допустимым выполнение повариантного подсчета запасов путем построения вложенной каркасной модели не для всего большого количества мелких тел, а для нескольких рудных тел наиболее представительных по количеству запасов. Для мелких же рудных тел при необходимости предлагается использовать менее трудоемкие, но менее точные методы подсчета запасов – блочное моделирование, подсчет с коэффициентом рудоносности и др.
Долевое (в процентах от общих запасов руды) распределение запасов руды по рудным телам на примере нескольких месторождений проиллюстрированы на рис.2.

Рис.2. Сектор круга соответствует относительной величине запасов в отдельно взятом рудном теле (каркасе).
Геологическая модель ресурсов и запасов – это динамическая система, эффективность которой определяется адекватностью применяемых методик и подходов. Специалист-геолог с высокой мерой квалификации и ответственности определяет сам допустимый баланс между достоверностью модели, эффективностью ее использования и трудозатратами на ее создание, а не должен жестко подчиняться требованиям государственной экспертизы. Данная статья – это некая «информационная вербальная модель» – краткое и несколько упрощенное представление определенных суждений и взглядов с целью сохранения информации и для обмена опытом. Несомненно, будет интересна также и другая точка зрения по вопросам, затрагиваемым в данной статье.
Об авторе
-0+0
Просмотров статьи: 3840, комментариев: 21
- Содержание сайта
- Комментарии
- Главная страница
Источник
Подсчет запасов – заключительная акция разведочных работ на месторождении.
Цели подсчета запасов:
1) определение количества полезного ископаемого с распределением его по типам и сортам руд, по категориям (А, В, С) запасов, по промышленному значению (балансовые и забалансовые);
2) определение качества полезного ископаемого, установление его технологических свойств;
3) анализ степени надежности подсчета запасов.
Все подсчитанные запасы полезных ископаемых представляются на рассмотрение и утверждение в ГКЗ или ТКЗ. При этом балансовые и забалансовые запасы подсчитываются и учитываются отдельно.
Кроме балансовых и забалансовых запасов выделяют:
Геологические запасы – запасы, подсчитанные в недрах Земли без учета потерь.
Эксплуатационные (промышленные) запасы – балансовые запасы, оставшиеся после вычета потерь в охранных целиках.
Извлекаемые запасы – это эксплуатационные запасы, оставшиеся после вычета эксплуатационных потерь, связанных с разубоживанием, несовершенством выбранной системы отработки, гидрогеологическими и другими условиями эксплуатации.
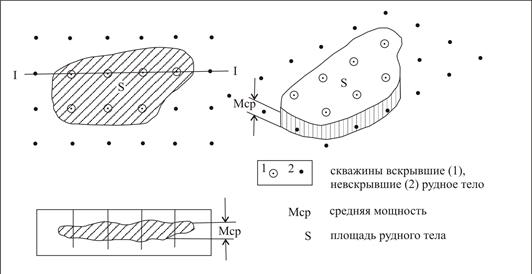
Исходные данные для подсчета запасов (методом блоков):
1) Площадь (месторождения, рудного тела, участка рудного тела), м2 (S);
2) Средняя мощность тела полезного ископаемого, м (m);
3) объемная масса полезного ископаемого, т/м3 (d);
4) среднее содержание полезного компонента, %, г/т (С).
Количество запасов (руды) полезного ископаемого вычисляется по формуле:
,
где V – объем блока, а d – объемная масса полезного ископаемого.
Количество запасов полезного компонента (металла) в руде определяется по формуле:
,
где P – запасы полезного компонента, а Ссред – среднее содержание полезного компонента в подсчитываемом объеме. В том случае, когда содержание полезного компонента выражено в процентах, используется формула:
.
Объем подсчетного блока вычисляется по формуле:
,
где S – площадь подсчетного блока, а M – его средняя мощность.
Если оконтуривание запасов произведено на горизонтальной проекции рудного тела, то объем его вычисляется как произведение площади проекции блока на его среднюю вертикальную мощность. Если оконтуривание произведено на про
дольной вертикальной проекции рудного тела, то объем его вычисляется как произведение площади проекции блока на его среднюю горизонтальную мощность.
Общие формулы для определения количества руды и количества металла выглядят следующим образом:
,
.
Площадь определяется на планах, разрезах, проекциях – планиметром, палеткой или по формулам простых геометрических фигур (треугольника, прямоугольника, трапеции и т. д.). Палетка представляет собой отрезок кальки, разбитой на квадраты с размером обычно 0,5 см. Такая палетка накладывается на геологический план, после чего подсчитывается количество квадратов, попавших на измеряемую площадь. Площадь подсчетного блока определяется по формуле:
,
где Sяч – площадь единичной ячейки (в масштабе), а K – количество ячеек. Sяч зависит от масштаба карты (плана). Например, если масштаб карты 1:1000, то в 1 см – 10 м, и Sяч = 25 м2.
Истинная площадь тел полезных ископаемых при наклонном их залегании всегда больше, чем ее проекция на горизонтальную или вертикальную плоскости. Она определяется по формулам:
, или
,
где Sист – истинная площадь рудного тела; Sгор – площадь рудного тела на горизонтальной проекции; Sверт – площадь рудного тела на вертикальной проекции; α – угол падения рудного тела.
Оконтуривание промышленного контура производится на горизонтальной проекции, если угол падения меньше 45º, и на вертикальной проекции, если этот угол больше 45º.
Это отчетливо видно на разрезах. При горизонтальном залегании рудное тело проектируется на горизонтальную плоскость без изменений; при наклонном залегании проекция рудного тела на горизонтальную и вертикальную плоскости будет всегда меньше истинных размеров рудного тела.
При подсчете запасов используют истинную мощность рудного тела. Так же, как и площадь, она связана с горизонтальной мощностью через угол падения рудного тела и определяется по формуле:
.
Средняя мощность определяется способом среднего арифметического по формуле:
,
где m1, m2…mn – значения мощности по отдельным горным выработкам или скважинам; n – количество выработок или скважин.
Среднее содержание полезного компонента определяется двумя способами:
1) методом расчета среднего арифметического (так же, как и мощность):
,
2) методом среднего взвешенного:
,
где C1, С2, Сn – содержание полезного компонента в каждой пробе;
M1, M2, Mn – длина интервала опробования.
Объемный вес (d) устанавливается по результатам технического опробования и рассчитывается методом среднего арифметического.
Методы подсчета запасов
Известно около 20 способов подсчета запасов, но в практике геологоразведочных работ используются, как правило, всего три способа: метод среднего арифметического, метод блоков и метод разрезов.
Метод среднего арифметического – в настоящее время используется крайне редко для подсчета запасов на месторождениях простого строения с горизонтальным залеганием тел полезных ископаемых, имеющих плитообразную форму и равномерное распределение полезных компонентов, разведанных относительно редкой сетью разведочных выработок. К ним относят месторождения угля, глин, песков, некоторые месторождения железа, алюминия и др. (первая группа сложности строения).
На месторождениях этого типа проводится, как правило, лишь внешний промышленный контур тел полезных ископаемых. При этом контуры тела сглаживаются путем превращения его в равновеликую по мощности плиту.
Средняя мощность и среднее содержание рассчитывается в целом по месторождению методом среднего арифметического с учетом всех кондиционных разведочных выработок по формулам:
,
,
где С1, С2, …, Сn – среденее содержание полезного компонента по разведочным выработкам; m1, m2, …, mn – значения мощности по разведочным выработкам; n – количество разведочных выработок. Среднее содержание полезного компонента по каждой разведочной выработке рассчитывается как среднее взвешенное на длину проб:
,
где С1, С2, …, Сn – содержание полезного компонента в каждой пробе;
L1, L2, …, Ln – длина отдельных проб.
Объемная масса (d) рассчитывается по ограниченному числу проб (20-30) также методом среднего арифметического. Запасы полезного ископаемого подсчитываются сразу по всему месторождению.
Преимущества данного способа: простота подсчета и быстрота.
Недостаток: невозможность выделения запасов по промышленным сортам.
Метод геологических блоков
Сущность метода состоит в том, что площадь месторождения разбивается на отдельные участки (блоки), в пределах каждого из которых основные параметры полезного ископаемого остаются постоянными, т. е. в отдельно взятом блоке должны быть одинаковыми или близкими по значению: мощность, содержание полезного компонента, густота разведочной сети, коэффициент вскрыши и т.п.
Месторождение в целом в этом случае представляет собой ряд сомкнутых пластин (блоков). В пределах каждого геологического блока основные исходные данные для подсчета запасов определяются средним арифметическим или средним взвешенным способами. Подсчет запасов по каждому блоку производится отдельно. Общие запасы по месторождению подсчитываются суммированием запасов по всем блокам отдельно по каждой категории A, B, C1 и С2.
Среднее содержание в целом по месторождению устанавливается обратным расчетом по формуле:
.
Выделение блоков на практике производится чаще всего по промышленным сортам и минеральным типам руд и по степени разведанности различных участков месторождения. При подсчете запасов этим способом используется специальный формуляр в виде таблицы.
| № блока | Категория запасов | Площадь блока, м2 | Средняя мощность рудных тел по блоку, м | Объем блока, м3 | Объемный вес, т/м3 | Запасы руды, т. | Среднее содержание полезного компонента в блоке, % | Запасы металла, т |
| В | 2,5 | |||||||
| С1 | 2,5 |
Достоинства метода:
1) позволяет выделять типы и сорта руд (подсчитывать запасы по типам и сортам руд);
2) простота подсчета и соответствующих графических построений.
Недостатки метода – подсчетные блоки часто не соответствуют по размерам эксплуатационным блокам, поэтому при эксплуатации месторождения приходится перестраивать подсчетные блоки и пересчитывать запасы.
Разновидностью метода геологических блоков является метод эксплуатационных блоков. О нем говорят в тех случаях, когда разведочные горные выработки впоследствии, при отработке месторождения, становятся эксплуатационными.
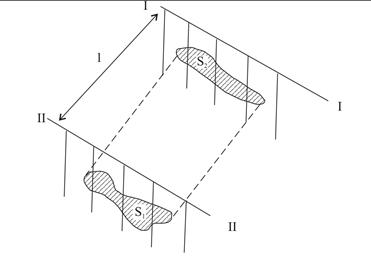
Метод геологических разрезов
Метод применяется при разведке месторождений, которые характеризуются изменчивыми мощностью и содержанием полезных компонентов. Сущность метода состоит в том, что тело полезного ископаемого разбивается на блоки, ограниченные разрезами (параллельными или нет), построенными по профилям разведочных выработок. Каждый блок, за исключением двух крайних, ограничен с двух сторон разрезами. Различают две разновидности метода:
1)вертикальных разрезов – используется при разведке месторождений, представленных рудными телами вытянутой, преимущественно плитовидной формы, разведанных скважинами при подчиненном участии горных выработок;
2) горизонтальных разрезов – используется при разведке месторождений, представленных штоко- и трубообразными телами, разведанными горными выработками при подчиненном участии скважин.
Среднее содержание в каждой разведочной выработке рассчитывается как среднее взвешенное на длину проб:
,
где С1, С2, …, Сn – содержание полезного компонента в каждой пробе;
L1, L2, …, Ln – длина отдельных проб.
Среднее содержание по разрезу (рассчитывается как среднее взвешенное на мощность рудного тела:
,
где С1, С2, …, Сn – содержание полезного компонента в каждой выработке;
M1, M2, …, Mn – мощность рудного тела в разведочной выработке.
Среднее содержание по блоку рассчитывается как среднее взвешенное на площадь рудного тела по разрезам по формуле:
.
Площадь сечений рудного тела определяется на разрезах палеткой или методом простых геометрических фигур, на которые разбивается рудное тело. При вычислении площади палетки учитывается, что разрезы часто имеют разные вертикальный и горизонтальный масштабы.
Объем блока рассчитывается по формулам:
1) ;
2) ;
где L – расстояние между разрезами. Вторая формула применяется в тех случаях, когда площади отличаются друг от друга на 40 % и более.
Запасы руды и металла подсчитывают по общепринятым формулам:
,
.
Достоинства метода:
1) простота и точность подсчета запасов;
2) возможность применения при практически любой форме тел полезного ископаемого (хотя чаще всего его используют при изометричной и линейной формах рудных тел).
Результаты подсчета запасов записываются в специальный табличный формуляр:
| № блока | № раз-реза | Категория запасов | Площадь блока S, м2 | Расстояние между разв. линиями L, м | Объем блока V, м3 | Объемная масса d, т/м3 | Запасы руды Q, т. | Среднее содержание полезн. к-та в блоке С, % | Запасы металла P, т |
| 1, 2 | С1 | 2,5 |
Достоверность подсчета запасов
Достоверность подсчета запасов зависит от:
1) изменчивости формы рудных тел и содержания полезного ископаемого. Чем сложнее месторождение, т.е., чем изменчивее мощность тел полезного ископаемого и содержание полезного компонента, тем больше расхождение между подсчитанными и действительными запасами.
2) детальности изучения месторождения. Чем гуще разведочная сеть, тем меньше будет погрешность в подсчете запасов. Она складывается из погрешностей определения площади рудных тел, их мощности, среднего содержания полезных компонентов, объемной массы и др.
Различают две группы ошибок при определении запасов: технические и геологические. Технические ошибки неизбежны, однако их влияние на достоверность запасов невелика. Сюда относятся ошибки замеров мощности, ошибки опробования, ошибки анализов, замеров расстояний и т.п. Геологические ошибки обусловлены тем, что при интерполяции и экстраполяции (при оконтуривании) допускается постепенное изменение формы тел и качества полезного ископаемого. Однако оруденение может быть и прерывистым, т.е. рудное тело может выклиниваться не плавно, а резко, и т. п.
Геологическая ошибка может быть систематической, когда, например, упрощается форма рудного тела при интерполяции (например, при неучете складчатой формы рудного тела и др.).
Источник
