Круговые процессы и их коэффициент полезного действия
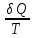
Круговым процессом, или циклом, называется такой процесс, когда система, пройдя через ряд промежуточных состояний, возвращается в исходное состояние. Графически круговой процесс изображен на рис. 6.8 замкнутой кривой и состоит из участка расширения (1а2) и сжатия (2b1).
Рис.6.8
Для расширения газу от тела с температурой Т1, называемого нагревателем, сообщается количество теплоты Q1. В процессе сжатия газ отдает количество теплоты Q2 телу с температурой Т2 < Т1, называемому холодильником.
Если цикл идет по часовой стрелке, то он называется прямым. Положительная работа расширения А, совершаемая газом и численно равная площади фигуры (V1 1a2V2), больше отрицательной работы сжатия А2, совершаемой над газом и выражаемой площадью фигуры (V2 2b1V1). Следовательно, работа А, совершенная за цикл и численно равная площади фигуры(1а2b1), будет положительна:
А = А1 – А2 > 0
Прямой цикл используется в тепловых машинах – периодически действующих устройствах, превращающих тепло, полученное от нагревателя, в работу А.
Так как в результате кругового процесса система возвращается в исходное состояние, то изменение внутренней энергии, как функции состояния, ΔU = 0.
Следовательно, согласно первого закона термодинамики (6.21) для кругового процесса
Q = A
Учитывая, что Q = Q1 – Q2, имеем:
А = Q1 – Q2
Определим термический коэффициент полезного действия цикла, как отношение работы А к полученной системой теплоте:
(6.46)
Может ли КПД теплового двигателя быть равен 100 %?
Это будет (согласно 6.46) только, если Q2 = 0. Как показал С. Карно, такое невозможно: для работы теплового двигателя необходимо часть тепла, полученного от нагревателя, отдать холодильнику. Это утверждение о невозможности создания теплового двигателя, работающего с одним только источником теплоты (вечный двигатель второго рода) составляет содержание второго закона термодинамики: невозможен вечный двигатель второго рода, т.е. процесс, единственным результатом которого было бы превращение теплоты, полученной от нагревателя, в работу.
Цикл (рис.6.8) может идти и против часовой стрелки. Тогда его работа будет отрицательна. Такой цикл называется обратным и используется вхолодильных машинах для переноса (за счет работы внешних сил) теплоты от тела с более высокой температурой к телу с температурой более низкой. Процесс перехода системы из состояния 1 в состояние 2 называется обратимым, если после возвращения системы в исходное состояние ни в системе, ни в окружающей среде никаких изменений не происходит. Любой процесс, не удовлетворяющий этим условиям, называется необратимым.
Все реальные процессы необратимы. Примером необратимости является процесс теплообмена, при котором теплота самопроизвольно переходит от горячего тела к холодному, однако обратного самопроизвольного процесса произойти не может.
Таким образом, обратимые процессы – понятие идеализированное. Однако их изучение важно, поскольку многие реальные процессы в природе и технике близки к обратимым, и именно они являются наиболее экономичными.
Цикл Карно
Основываясь на втором законе термодинамики, С. Карно доказал, что из всех тепловых машин наибольшим КПД обладают обратимые машины. Самым экономичным является круговой процесс, состоящий из двух изотерм и двух адиабат (рис.6.9), названный циклом Карно.
Можно показать, что КПД цикла Карно определяется только температурами нагревателя Т1 и холодильника Т2:
(6.47)
Рис.6.9
Как следует из (6.47), для повышения η необходимо увеличивать разность температур Т1 нагревателя и Т2 холодильника.
Энтропия
Из формул (6.46) и (6.47) следует, что и
Учтем, что количество тепла Q2, отданного холодильнику отрицательно. Тогда последнее равенство можно записать:
(6.48)
Отношение Q/T называется приведенной теплотой.
Приведенная теплота, переданная системе нагревателем, при бесконечно малом ее изменении, равна δQ/Т. Можно показать, что для любого обратимого кругового процесса сумма приведенных теплот равна нулю. Тогда выражение (6.48) в общем, виде может быть записано как:
(6.49)
Равенство нулю интеграла по замкнутому контуру означает, что в обратимом процессе подинтегральное выражение есть полный дифференциал некоторой функции S, зависящей только от состояния системы. Функция S называется энтропией.
Таким образом
(6.50)
Из формулы (6.49) следует, что для обратимых процессов изменение энтропии
ΔS = 0 (6.51)
Можно показать, что для необратимых неравновесных процессов, происходящих в замкнутой системе, энтропия возрастает
ΔS > 0 (6.52)
Соотношения (6.51) и (6.52) объединяются в неравенство Клаузиса:
ΔS≥0
т.е. энтропия замкнутой системы либо возрастает, либо остается постоянной.
Так как реальные процессы необратимы, то можно утверждать, что все процессы, протекающие в замкнутой системе, ведут к увеличению энтропии. Это утверждение, называемое принципом возрастания энтропии, является еще одной формулировкой второго закона термодинамики.
Физический смысл энтропии выяснил Л. Больцман, который показал, что энтропия связана с термодинамической вероятностью состояния системы. Термодинамическая вероятность w определяется как число способов, которыми может быть реализовано данное состояние системы. Согласно Больцману, связь S и w выражается формулой:
S = k lnw (6.53)
где k – постоянная Больцмана.
Когда достигается равновесное состояние системы, то в этом состоянии система может оставаться сколь угодно долго, т.е. параметры системы не меняются и в системе отсутствуют потоки энергии или вещества. Если потоки имеют место, то изменение внутренней энергии dU может происходить не только за счет сообщения системе теплоты δQ и совершения над ней работы δА, но и за счет переноса массы. Тогда первый закон термодинамики можно записать в более общей форме
dU = δQ – PdV + μdn,
где называется химическим потенциалом и представляет изменение энергии системы, приходящейся на одну частицу, участвующей в переносе при V = const и S = const.
Фазовые превращения
Фазой называется термодинамически равновесное состояние вещества, отличаются не химическим составом, а физическим свойствами от других равновесных состояний того же вещества (например, вода может находиться в трех фазах: жидком, твердом и в виде пара). Переход вещества из одной фазы в другую называется фазовым переходом.
Различают фазовые переходы I и II рода. Фазовый переход I рода связан с поглощением или выделением тепла (например, плавление и кристаллизация). Фазовый переход II рода не связаны с теплотой (например, переход некоторых веществ при определенных температурах в сверхпроводящее состояние см. п.5.7).
Для характеристики фазовых переходов используются диаграммы состояний (обычно в координатах Р – Т). На этих диаграммах можно найти точку одновременного равновесного осуществления трех фаз – тройную точку. Например, тройная точка для воды 273,16 К. Термодинамика позволяет рассчитать равновесие двух фаз одного вещества, пользуясь уравнением Клапейрона – Клаузиуса:
,
где производная от равновесного давления по температуре зависит от теплоты фазового перехода λ, температуры перехода и изменения объема фаз (например, при замерзании воды ее объем возрастает).
Источник
В
результате кругового процесса система
возвращается в исходное состояние,
следовательно, полное изменение
внутренней энергии равно нулю. Поэтому,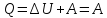 т.е. работа, совершаемая за цикл, равна
т.е. работа, совершаемая за цикл, равна
количеству полученной извне теплоты.
Если в ходе кругового процесса система
не только получает количество теплоты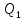 ,
,
но и теряет (отдает) количество теплоты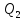 ,
,
то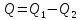 .
.
Термический
коэффициент полезного действия для
кругового процесса – это величина,
равная отношению работы, совершенной
системой, к количеству теплоты, полученному
в этом цикле системой:
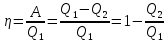 .
.
(40.1)
§ 41. Энтропия
«Энтропия»
в переводе с греческого означает поворот,
превращение. Это понятие введено в
термодинамику немецким ученым Р.
Клаузиусом как мера необратимого
рассеяния энергии.
Количество
теплоты
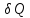 ,
,
которое должно быть доставлено системе
или отнято у неё при переходе от одного
состояния в другое, не определяется
однозначно начальным и конечным
состояниями, но существенно зависит от
способа осуществления этого перехода
.
Однако,
приведенное количество теплоты –
отношение теплоты
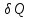 к температуре
к температуре
Т
системы при бесконечно малых изменениях
состояния системы – есть функция
состояния системы.
В любом
обратимом круговом процессе
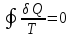 .
.
Следовательно, подынтегральное выражение
есть полный дифференциал некоторой
функции, которая определяется только
начальным и конечным состояниями системы
и не зависит от пути, каким система
пришла в это состояние.
Энтропией
Sназывается
функция состояния системы, дифференциалом
которой является
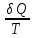 :
:
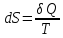 .
.
(41.1)
Таким
образом, первое начало термодинамики
можно записать в виде
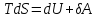 ,
,
откуда
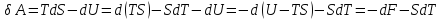
Функция
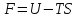 является функцией состояния системы и
является функцией состояния системы и
называется энергией Гельмгольца или
свободной энергией.
Изменение
энтропии.
В
замкнутой системе для обратимых процессов
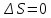 ;
;
для необратимых процессов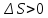 .
.
Энтропия
замкнутой системы может либо возрастать
(в случае необратимых процессов) либо
оставаться постоянной (в случае обратимых
процессов):
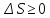
– неравенство
Клаузиуса.
Поскольку
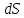 и
и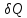 имеют один и тот же знак, то по характеру
имеют один и тот же знак, то по характеру
изменения энтропии можно судить о
направлении процесса теплообмена.
При
нагревании тела
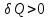 и его энтропия возрастает
и его энтропия возрастает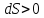 ,
,
при охлаждении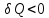 и энтропия убывает
и энтропия убывает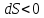 .
.
Принцип
возрастания энтропии:Все
процессы в замкнутой системе ведут к
увеличению её энтропии. В замкнутой
системе идут в направлении от менее
вероятных состояний к более вероятным,
до тех пор, пока вероятность состояния
не станет максимальной. В состоянии
равновесия – наиболее вероятного
состояния системы- число микросостояний
максимально, при этом максимальна и
энтропия.
§ 42. Второе начало термодинамики
Выражая
всеобщий закон сохранения и превращения
энергии, первое начало термодинамики
не позволяет определить направление
протекания процесса. В самом деле,
процесс самопроизвольной передачи
энергии в форме теплоты от холодного
тела к горячему, ни в какой мере не
противоречит первому закону термодинамики.
Однако при опускании раскаленного куска
железа в холодную воду никогда не
наблюдается явление дальнейшего
нагревания железа за счет соответствующего
охлаждения воды. Далее, первое начало
не исключает возможности такого процесса,
единственным результатом которого было
бы превращение теплоты, полученной от
нагревателя в эквивалентную ей работу.
Так, например, основываясь на первом
начале можно было бы попытаться построить
периодически действующий двигатель,
совершающий работу за счет одного
источника тепла (например, за счет
внутренней энергии океана). Такой
двигатель называется вечным двигателем
второго рода. Обобщение огромного
экспериментального материала привело
к выводу о невозможности построения
вечного двигателя второго рода. Этот
вывод получил название второго начала
термодинамики.
Существует
ряд различных по форме, одинаковых по
существу формулировок второго начала:
Невозможен
процесс, единственным результатом
которого является превращение всей
теплоты, полученной от нагревателя, в
эквивалентную ей работу.Формулировка
Клаузиуса: теплота сама собой не может
переходить от менее нагретого тела к
более нагретому.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник

Круговые процессы, их к.п.д.
Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное.
Круговые процессы называется прямым, если его результатом является совершение работы над внешними телами и переход определённого количества теплоты от более нагретого тела (нагревателя) к менее нагретому (холодильнику).
Термический к.п.д. в круговых процессах определяется по формуле
К.п.д. идеального и реального цикла Карно.
В термодинамике цикл Карно — это обратимый круговой процесс, состоящий из двух адиабатических и двух изотермических процессов. В процессе Карно термодинамическая система выполняет механическую работу и обменивается теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником.
Коэффициент полезного действия тепловой машины Карно равен
Из последнего выражения следует, что КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела. Этот результат составляет содержание первой теоремы Карно. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля, а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.
К.п.д. цикла Карно одинаков и для идеального и для реального газа.
Билет 21
2.11. самоиндукция, ее объяснение.Формула э.д.с самоиндукции
Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока наз-ся самоиндукцией.
Замыкание цепи
При замыкании в эл.цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи ( вихревое поле тормозит электроны).
В результате Л1 загорается позже, чем Л2.
Размыкание цепи
При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток ( стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи.
В результате Л при выключении ярко вспыхивает.
в электротехнике явление самоиндукции проявляется при замыкании цепи (эл.ток нарастает постепенно) и при размыкании цепи (эл.ток пропадает не сразу)
.ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.
3.7
Осуществление интерференции света от обычных источников света.
Интерференция света на тонкой пленке. Условия максимумов и минимумов интерференции света на пленке в отраженном и в проходящем свете.
Интерференционные полосы равной толщины и интерференционные полосы равного наклона.
1)Явление интерференции наблюдается в тонком слое несмешивающихся жидкостей (керосина или масла на поверхности воды), в мыльных пузырях, бензине, на крыльях бабочек, в цветах побежалости, и т. д.
2) интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённыхобъективов. Луч света, проходя через плёнку толщиной , отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, отчего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при , где — длина волны. Если нм, то толщина плёнки равняется 550:4=137,5 нм.
Лучи соседних участков спектра по обе стороны от нм интерферируют не полностью и только ослабляются, отчего плёнка приобретает окраску. В приближении геометрической оптики, когда есть смысл говорить об оптической разности хода лучей, для двух лучей
— условие максимума;
— условие минимума,
где k=0,1,2… и — оптическая длина пути первого и второго луча, соответственно.
3)Полосы равного наклона
Особенно важен частный случай интерференции света, отраженного двумя поверхностями плоскопараллельной пластинки, когда точка наблюдения P находится в бесконечности, т.е. наблюдение ведется либо глазом, аккомодированным на бесконечность, либо на экране, расположенном в фокальной плоскости собирающей линзы (рис. 8.8).
Рис. 8.8
В этом случае оба луча, идущие от S к P, порождены одним падающим лучом и после отражения от передней и задней поверхностей пластинки параллельны друг другу. Оптическая разность хода между ними в точкеP такая же, как на линии DC:
.
Здесь n – показатель преломления материала пластинки. Предполагается, что над пластинкой находится воздух, т.е. . Так как , (h – толщина пластинки, и – углы падения и преломления на верхней грани; ), то для разности хода получаем
.
Следует также учесть, что при отражении волны от верхней поверхности пластинки в соответствии с формулами Френеля ее фаза изменяется на π. Поэтому разность фаз δ складываемых волн в точке P равна:
,
где – длина волны в вакууме.
В соответствии с последней формулой светлые полосы расположены в местах, для которых , где m – порядок интерференции. Полоса, соответствующая данному порядку интерференции, обусловлена светом, падающим на пластинку под вполне определенным углом α. Поэтому такие полосы называют интерференционными полосами равного наклона. Если ось объектива расположена перпендикулярно пластинке, полосы имеют вид концентрических колец с центром в фокусе, причем в центре картины порядок интерференции максимален.
Полосы равного наклона можно получить не только в отраженном свете, но и в свете, прошедшем сквозь пластинку. В этом случае один из лучей проходит прямо, а другой – после двух отражений на внутренней стороне пластинки. Однако видимость полос при этом низкая.
Для наблюдения полос равного наклона вместо плоскопараллельной пластинки удобно использовать интерферометр Майкельсона (рис. 8.9). Рассмотрим схему интерферометра Майкельсона: з1 и з2 – зеркала. Полупрозрачное зеркало посеребрено и делит луч на две части – луч 1 и 2. Луч 1, отражаясь от з1 и проходя , дает , а луч 2, отражаясь от з2 и далее от , дает . Пластинки и одинаковы по размерам. ставится для компенсации разности хода второго луча. Лучи и когерентны и интерферируют.
Рис. 8.9
Дата добавления: 2017-02-25; просмотров: 689 | Нарушение авторских прав | Изречения для студентов
Читайте также:
Рекомендуемый контект:
Поиск на сайте:
© 2015-2020 lektsii.org – Контакты – Последнее добавление
Источник
