Коэффициент полезного действия подвижного блока можно увеличить

Словом «полезное» в физике является эффект после сопротивления. Ярким примером можно назвать сопротивление металла обрабатывающему станку, для подъемного крана  – масса объекта. Например, КПД обычной лампы накапливания не превышает 5%, когда светодиодные имеют гораздо выше. Это происходит потому что большая часть потребляемой энергии уходит на генерирование теплоты, а не света.

Подобное есть и в электронике и этот коэффициент необходимо учитывать при проектировании плат, электросхем. Здесь важно учитывать сопротивление проводимости металла и использовать материалы имеющие меньшее сопротивление. В статье будут рассмотрены основные аспекты КПД, как его рассчитывать, на что он влияет и какие есть основные возможности, чтобы его увеличить.

Что такое КПД

Коэффициент полезного действия (кпд) – отношение полезно используемой энергии Wп, напр. в виде работы, к общему кол-ву энергии W, получаемой системой (машиной или двигателем), Wп/W. Из-за неизбежных потерь энергии на трение и др. неравновесные процессы для реальных систем всегда. На основании второго начала термодинамики для тепловых машин наибольший кпд (отношение работы Wп, совершаемой за один цикл, к кол-ву подведённой к ней за этот цикл теплоты Q)зависит только от темп-ры нагревателя T1 и холодильника Т2 и равен = Wп/Q= (Т1- T2/T1(Карно теорема).

Для электрич. двигателей кпд равен отношению полезной механич. работы к электрич. энергии, получаемой от источника; в электрич. трансформаторах кпд – отношение эл–магн. энергии, получаемой во вторичной обмотке, к энергии, потребляемой в первичной обмотке. Понятие кпд имеет общий характер и применимо к разл. системам: электрич. генераторам, двигателям разного рода, полупроводниковым приборам, биол. объектам, поэтому оно может служить для сравнительной оценки эффективности разнообразных процессов.

Интересно почитать: Что такое закон Джоуля-Ленца.

Мощность и коэффициент полезного действия электродвигателей

Электрические двигатели имеют высокий коэффициент полезного действия (КПД), но все же он далек от идеальных показателей, к которым продолжают стремиться конструкторы. Все дело в том, что при работе силового агрегата преобразование одного вида энергии в другой проходит с выделение теплоты и неминуемыми потерями. Рассеивание тепловой энергии можно зафиксировать в разных узлах двигателя любого типа. Потери мощности в электродвигателях являются следствием локальных потерь в обмотке, в стальных деталях и при механической работе. Вносят свой вклад, пусть и незначительный, дополнительные потери.

Магнитные потери мощности

При перемагничивании в магнитном поле сердечника якоря электродвигателя происходят магнитные потери. Их величина, состоящая из суммарных потерь вихревых токов и тех, что возникают при перемагничивании, зависят от частоты перемагничивания, значений магнитной индукции спинки и зубцов якоря. Немалую роль играет толщина листов используемой электротехнической стали, качество ее изоляции.

Механические и электрические потери

Механические потери при работе электродвигателя, как и магнитные, относятся к числу постоянных. Они складываются из потерь на трение подшипников, на трение щеток, на вентиляцию двигателя. Минимизировать механические потери позволяет использование современных материалов, эксплуатационные характеристики которых совершенствуются из года в год. В отличие от них электрические потери не являются постоянными и зависят от уровня нагрузки электродвигателя. Чаще всего они возникают вследствие нагрева щеток, щеточного контакта.

Добавочные потери

Добавочные потери мощности в электродвигателях складываются из потерь, возникающих в уравнительных соединениях, из потерь из-за неравномерной индукции в стали якоря при высокой нагрузке. Вносят свой вклад в общую сумму добавочных потерь вихревые токи, а также потери в полюсных наконечниках. Точно определить все эти значения довольно сложно, поэтому их сумму принимают обычно равной в пределах 0,5-1%. Эти цифры используют при расчете общих потерь для определения КПД электродвигателя.

КПД и его зависимость от нагрузки

Коэффициент полезного действия (КПД) электрического двигателя это отношение полезной мощности силового агрегата к мощности потребляемой. Этот показатель у двигателей, мощностью до 100 кВт находится в пределах от 0,75 до 0,9. для более мощных силовых агрегатов КПД существенно выше: 0,9-0,97. Определив суммарные потери мощности в электродвигателях можно достаточно точно вычислить коэффициент полезного действия любого силового агрегата. Этот метод определения КПД называется косвенным и он может применяться для машин различной мощности.

Достигает он пикового значения быстро и уверенно, но после своего максимума начинает медленно уменьшаться. Это связывают с возрастанием электрических потерь при нагрузках, более 80% от номинальной мощности. Падение коэффициента полезного действия не велико, что позволяет говорить о высоких показателях эффективности электродвигателей в широком диапазоне мощностей.

В чем измеряется КПД

Коэффициент полезного действия (кпд), характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии; определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно h = Wпол/Wcyм.

В электрических двигателях кпд — отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника; в тепловых двигателях — отношение полезной механической работы к затрачиваемому количеству теплоты; в электрических трансформаторах — отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой.

Интересно почитать: Как образуется статическое электричество.

Для вычисления кпд разные виды энергии и механическая работа выражаются в одинаковых единицах на основе механического эквивалента теплоты, и др. аналогичных соотношений. В силу своей общности понятие кпд позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т. д.

Из-за неизбежных потерь энергии на трение, на нагревание окружающих тел и т. п. кпд всегда меньше единицы. Соответственно этому кпд выражается в долях затрачиваемой энергии, т. е. в виде правильной дроби или в процентах, и является безразмерной величиной. Кпд тепловых электростанций достигает 35—40%, двигателей внутреннего сгорания — 40—50%, динамомашин и генераторов большой мощности—95%, трансформаторов—98%.

Кпд процесса фотосинтеза составляет обычно 6—8%, у хлореллы он достигает 20—25%. У тепловых двигателей в силу второго начала термодинамики кпд имеет верхний предел, определяемый особенностями термодинамического цикла (кругового процесса), который совершает рабочее вещество. Наибольшим кпд обладает Карно цикл. Различают кпд отдельного элемента (ступени) машины или устройства и кпд, характеризующий всю цепь преобразований энергии в системе. Кпд первого типа в соответствии с характером преобразования энергии может быть механическим, термическим и т. д. Ко второму типу относятся общий, экономический, технический и др. виды кпд. Общий кпд системы равен произведению частных кпд, или кпд ступеней.

В технической литературе кпд иногда определяют т. о., что он может оказаться больше единицы. Подобная ситуация возникает, если определять кпд отношением Wпол/Wзатр, где Wпол — используемая энергия, получаемая на «выходе» системы, Wзатр — не вся энергия, поступающая в систему, а лишь та её часть, для получения которой производятся реальные затраты.

Например, при работе полупроводниковых термоэлектрических обогревателей (тепловых насосов) затрата электроэнергии меньше количества теплоты, выделяемой термоэлементом. Избыток энергии черпается из окружающей среды. При этом, хотя истинный кпд установки меньше единицы, рассмотренный кпд h = Wпол/Wзатр может оказаться больше единицы.

Для чего нужен расчет КПД

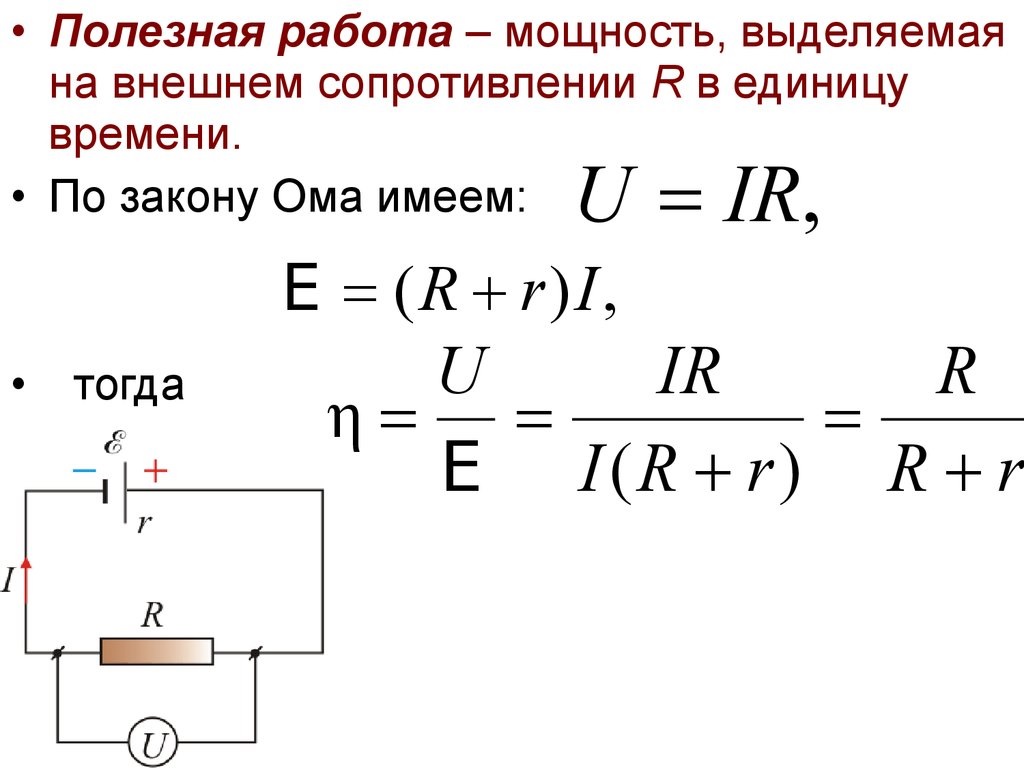
Коэффициент полезного действия электрической цепи – это отношение полезного тепла к полному. Для ясности приведем пример. При нахождении КПД двигателя можно определить, оправдывает ли его основная функция работы затраты потребляемого электричества. То есть его расчет даст ясную картину, насколько хорошо устройство преобразовывает получаемую энергию. Обратите внимание! Как правило, коэффициент полезного действия не имеет величины, а представляет собой процентное соотношение либо числовой эквивалент от 0 до 1. КПД находят по общей формуле вычисления, для всех устройств в целом. Но чтобы получить его результат в электрической цепи, вначале потребуется найти силу электричества.

По физике известно, что любой генератор тока имеет свое сопротивление, которое еще принято называть внутренняя мощность. Помимо этого значения, источник электричества также имеет свою силу. Дадим значения каждому элементу цепи: сопротивление – r; сила тока – Е; резистор (внешняя нагрузка) – R. Полная цепь Итак, чтобы найти силу тока, обозначение которого будет – I, и напряжение на резисторе – U, потребуется время – t, с прохождением заряда q = lt. Рассчитать работу источника тока можно по следующей формуле: A = Eq = EIt. В связи с тем, что сила электричества постоянна, работа генератора целиком преобразуется в тепло, выделяемое на R и r. Такое количество можно рассчитать по закону Джоуля-Ленца: Q = I2 + I2 rt = I2 (R + r) t.

Затем приравниваются правые части формулы: EIt = I2 (R + r) t. Осуществив сокращение, получается расчет: E = I(R + r). Произведя у формулы перестановку, в итоге получается: I = E R + r. Данное итоговое значение будет являться электрической силой в данном устройстве. Произведя таким образом предварительный расчет, теперь можно определить КПД.

Расчет КПД электрической цепи Мощность, получаемая от источника тока, называется потребляемой, определение ее записывается – P1. Если эта физическая величина переходит от генератора в полную цепь, она считается полезной и записывается – Р2. Чтобы определить КПД цепи, необходимо вспомнить закон сохранения энергии.

В соответствии с ним, мощность приемника Р2 будет всегда меньше потребляемой мощности Р1. Это объясняется тем, что в процессе работы в приемнике всегда происходит неизбежная пустая трата преобразуемой энергии, которая расходуется на нагревание проводов, их оболочки, вихревых токов и т.д. Чтобы найти оценку свойств превращения энергии, необходим КПД, который будет равен отношению мощностей Р2 и Р1.

Итак, зная все значения показателей, составляющих электроцепи, находим ее полезную и полную работу: А полезная. = qU = IUt =I2Rt; А полная = qE = IEt = I2(R+r)t. В соответствии этих значений, найдем мощности источника тока: Р2 = А полезная /t = IU = I2 R; P1 = А полная /t = IE = I2 (R + r). Произведя все действия, получаем формулу КПД: n = А полезная / А полная = Р2 / P1 =U / E = R / (R +r). У этой формулы получается, что R выше бесконечности, а n выше 1, но при всем этом ток в цепи остается в низком положении, и его полезная мощность мала.

Каждый желает найти КПД повышенного значения. Для этого необходимо найти условия, при которых P2 будет максимален. Оптимальные значения будут: dP2 / dR = 0. Далее определить КПД можно формулами: P2 = I2 R = (E / R + r)2 R; dP2 / dR = (E2 (R + r)2 — 2 (r + R) E2 R) / (R + r)4 = 0; E2 ((R + r) -2R) = 0. В данном выражении Е и (R + r) не равны 0, следовательно, ему равно выражение в скобках, то есть (r = R). Тогда получается, что мощность имеет максимальное значение, а коэффициент полезного действия = 50 %. Как видно, найти коэффициент полезного действия электрической цепи можно самостоятельно, не прибегая к услугам специалиста. Главное –соблюдать последовательность в расчетах и не выходить за рамки приведенных формул.

Примеры расчета КПД

Пример 1. Нужно рассчитать коэффициент для классического камина. Дано: удельная теплота сгорания березовых дров – 107Дж/кг, количество дров – 8 кг. После сгорания дров температура в комнате повысилась на 20 градусов. Удельная теплоемкость кубометра воздуха – 1,3 кДж/ кг*град. Общая кубатура комнаты – 75 кубометров.

Чтобы решить задачу, нужно найти частное или отношение двух величин. В числителе будет количество теплоты, которое получил воздух в комнате (1300Дж*75*20=1950 кДж ). В знаменателе – количество теплоты, выделенное дровами при горении (10000000Дж*8 =8*107 кДж). После подсчетов получаем, что энергоэффективность дровяного камина – около 2,5%. Действительно, современная теория об устройстве печей и каминов говорит, что классическая конструкция не является энергоэффективной. Это связано с тем, что труба напрямую выводит горячий воздух в атмосферу.

Для повышения эффективности устраивают дымоход с каналами, где воздух сначала отдает тепло кладке каналов, и лишь потом выходит наружу. Но справедливости ради, нужно отметить, что в процессе горения камина нагревается не только воздух, но и предметы в комнате, а часть тепла выходит наружу через элементы, плохо теплоизолированные – окна, двери и т.д.

Пример 2. Автомобиль проделал путь 100 км. Вес машины с пассажирами и багажом – 1400 кг. При этом было затрачено14 литров бензина. Найти: КПД двигателя.

Для решения задачи необходимо отношение работы по перемещению груза к количеству тепла, выделившемуся при сгорании топлива. Количество тепла также измеряется в Джоулях, поэтому не придется приводить к другим единицам. A будет равна произведению силы на путь( A=F*S=m*g*S). Сила равна произведению массы на ускорение свободного падения. Полезная работа = 1400 кг x 9,8м/с2 x 100000м=1,37*108 Дж

Удельная теплота сгорания бензина – 46 МДж/кг=46000 кДж/кг. Восемь литров бензина будем считать примерно равными 8 кг. Тепла выделилось 46*106*14=6.44*108 Дж. В результате получаем η ≈21%.