Коэффициент полезного действия неподвижного блока формула
Блоки −− простые механические устройства, позволяющие регулировать силу. Любой блок представляет собой колесо с желобом по окружности, вращающееся вокруг своей оси. Если ось является неподвижной, то блок называется неподвижным. Если ось является подвижной, то блок называется подвижным. Желоб предназначен для каната, цепи, ремня и т. п.
Неподвижный блок.
Действие неподвижного блока аналогично действию рычага с равными плечами l1=l2=r. Приложенная сила F1 равна нагрузкеF2, и условие равновесия имеет вид:
F1 = F2.
Неподвижный блок применяют, когда нужно изменить направление силы, не меняя ее величину.
Подвижный блок.
Подвижный блок действует аналогично рычагу, плечи которого составляют: l2 = l1 /2 = r. При этом условие равновесия имеет вид:
.
где F1 — приложенная сила, F2 — нагрузка. Применение подвижного блока дает выигрыш в силе в два раза.
Расчет колодочного тормоза с приводом от электрогидравлического толкателя.
Расчетная схема колодочного тормоза ТКТ с пружинным замыканием
Рис. 1
Максимально допустимый установочный зазор между колодкой и шкивом:
где hм — ход якоря электромагнита; k1 — коэффициент возможного использования хода якоря.
Из условия равновесия верхнего рычага, соединяющего правый рычаг с замыкающей пружиной и со штоком толкателя, определяется необходимая сила сжатия пружины:
При размыкании тормоза сила толкателя Р преодолевает силу сжатия пружины Рп; при этом Рт = Рпc/e.
Необходимый ход штока толкателя hт определяется из уравнения:
На рисунке 2 размер hт — полный ход штока, указанный в паспорте, размер h — установочный рабочий ход штока.
Колодочный тормоз с электрогидравлическим приводом
Рис. 2
Значения минимальных радиальных установочных зазоров между колодкой и шкивом принимают по следующим рекомендациям:
Табл. 1
Жесткость рычажной системы необходимо проверять расчетом. Суммарная деформация рычажной системы независимо от вида привода не должна быть более 10% нормального хода штока.
Расчет тормозных рычагов на прочность ведется по изгибающему моменту М от силы Р в опасном сечении рычага:
где W — момент сопротивления изгибу рассчитываемого сечения рычага; kд — динамический коэффициент, учитывающий характер изменения приложенной силы при замыкании тормоза, и в зависимости от типа привода колодочного тормоза (см. остановы и тормоза) имеет следующие значения:
Грузовые барабаны ГПМ. Расчет габаритов барабана при многочисленной навивке каната.
Барабаны – это элементы грузоподъемных машин, служащие для наматывания гибкого органа и преобразования вращательного движения привода в поступательное движение груза. Барабаны разделяются на цепные и канатные для одинарных и сдвоенных полиспастов.
Канатные барабаны по форме внешней поверхности разделяют на цилиндрические, конические и коноидальные. Наибольшее распространение получили цилиндрические барабаны. Они бывают гладкие и нарезные.
Гладкие барабаны применяют для многослойной навивки каната при большой высоте подъема груза и необходимости уменьшения длины барабана по условиям компоновки. Однако у канатов, наматываемых на гладкие барабаны, появляются большие контактные напряжения в местах касания и происходит сплющивание каната при намотке в несколько слоев, что значительно снижает срок их службы. Барабаны изготавливают отливкой или сваркой.
Толщину стенки барабанапринимают по эмпирической зависимости: d = 0,02 D + (6 10) мм – для чугунных барабанов и d = 0,01 D + 3 мм – для стальных, где D – диаметр барабана по дну канавки, мм
РАСЧЕТ
При той же длине каната многослойная навивка позволяет применять барабаны меньшей длины, чем при однослойной навивке, однако условия работы каната в этом случае резко ухудшаются, уменьшается срок его службы, не обеспечивается равномерность хода груза; скорость перемещения груза получается различной при навивании первого и каждого из последующих слоев. Барабаны для многослойной навивки делают с гладкой поверхностью и бортами, предотвращающими сход каната. Высота бортов ho :
h0=(m+2)dК
где h0–высота бортов барабана; dк–диаметр каната;
При заданной канатоемкости LК, диаметре каната dК, диаметре барабана DБ, шаге навивки, равном dК, числе навиваемых слоев m, Длина барабана с гладкой поверхностью :
LБ=LКdК/πm(mdК+DБ)
Канатоёмкость барабана зависит от длины и диаметра барабана LБ и DБ , количества слоёв навивки каната на барабане m и диаметр каната dк, которые выбираются из паспорта. Канатоёмкостьопределяют, м
LК=(πzm( DБ dК)-2π DБ )/1000
где z – число витков каната на рабочей длине барабана, z = LБ/t ; t – шаг навивки каната, t =d .
Источник

1. Простые механизмы — приспособления, которые сконструировал и использовал человек, чтобы облегчить работу по перемещению тяжёлых предметов. К ним относят: рычаг, блок, наклонную плоскость. Разновидностями этих механизмов являются: клин, ворот и винт.
Все простые механизмы позволяют преобразовать силу, действующую на тело: либо уменьшить её, либо изменить её направление.
2. Рычаг — это стержень, вращающийся вокруг неподвижной опоры или оси (рис. 51). На рисунке показан рычаг, который может вращаться вокруг точки О, расположенный между концами рычага. К одному концу рычага подвешен груз, действующий на рычаг с силой ( F_1 ), равной весу груза. Действуя на длинный конец рычага с силой ( F_2 ), человек поднимает груз. При этом сила ( F_1 ) стремится повернуть рычаг по часовой стрелке, а груз ( F_2 ) — против часовой стрелки.
Плечом силы называют кратчайшее расстояние (перпендикуляр) от точки опоры до линии действия силы. Так, плечом силы ( F_1 ) является расстояние ОА ( (l_1) ), плечом силы ( F_2 ) — расстояние ОВ ( (l_2) ).
Из эксперимента следует, что рычаг находится в равновесии, если произведение силы, вращающей рычаг по часовой стрелке, и её плеча равно произведению силы, вращающей рычаг против часовой стрелки, и её плеча, т.е. ( F_1l_1=F_2l_2 ). Произведение силы, действующей на рычаг, и её плеча называют моментом силы: ( Fl=M ). Соответственно, если рычаг находится в равновесии, то ( M_1=M_2 ).
Условие равновесия рычага можно записать по-другому:( frac{F_1}{F_2}=frac{l_2}{l_1} ). Это равенство означает, что рычаг находится в равновесии, если силы, действующие на него, обратно пропорциональны их плечам. Оно называется условием равновесия рычага.
Рычаг другого типа вращается вокруг точки, находящейся на конце рычага. Примером такого рычага может служить тачка. Когда используется такой рычаг, то вес груза направлен вниз, а человек действует на свободный конец рычага с силой, направленной вверх. Для такого рычага также справедливо условие равновесия, приведенное выше.
3. При подъеме груза работа силы, действующей на груз, равна ( A_1=F_1h_1 ), работа силы, приложенной к другому концу рычага, равна ( A_2=F_2h_2 ). Рассмотрение треугольников AOC и BOD позволяет сделать вывод о том, что они подобны и ( frac{AO}{BO}=frac{AC}{BD} ) или ( frac{l_1}{l_2}=frac{h_1}{h_2} ). Поскольку ( F_1l_1=F_2l_2 ), то ( F_1h_1=F_2h_2 ), т.е. ( A_1=2 ). Таким образом, рычаг, позволяя выиграть в силе, не даёт выигрыша в работе.
4. Ещё одним простым механизмом является блок. Блок — это колесо с желобом, по которому пропускается трос и которое может вращаться относительно оси О (см. рис. ниже).
Если ось блока закреплена, то блок не перемещается, и он называется неподвижным.
Неподвижный блок можно рассматривать как рычаг, вращающийся вокруг точки, лежащей посередине рычага. Плечи такого рычага равны друг другу: OA = OB. В соответствии с условием равновесия рычага приложенные к блоку силы тоже равны: ( P=F ). Следовательно, неподвижный блок не даёт выигрыша в силе, но он позволяет поднимать груз, прикладывая силу, направленную не вверх, а вниз, что облегчает перемещение груза.
Чтобы получить выигрыш в силе используют подвижный блок (рис. 53). К нему непосредственно прикрепляется груз, один конец троса закрепляется, а к другому прикладывают силу и, таким образом, перебирая трос, поднимают блок с грузом.
В этом случае точкой вращения блока является точка А (см. рис. 52).
Плечи действующих сил равны соответственно: AO и AB, при этом AB = 2AO. В соответствии с условием равновесия рычага: ( P=2F ). Таким образом, подвижный блок даёт выигрыш в силе в 2 раза: ( F=P/2 ).
Измерив расстояние ( h_1 ), которое проходит груз, и расстояние ( h_2 ), на которое перемещается конец троса, можно обнаружить, что расстояние ( h_2=2h_1 ). Таким образом, подвижный блок даёт выигрыш в силе в 2 раза и в 2 раза проигрыш в пути. Соответственно, работа ( Ph_1=Fh_2 ), т.е. ( A_1=2 ). Подвижный блок, так же как и рычаг, не даёт выигрыша в работе.
5. Наклонная плоскость используется в том случае, если нужно поднять объемный тяжёлый груз на какую-либо высоту (рис. 54).
Например, нужно погрузить ящик с металлическими деталями в кузов грузовика. В этом случае кладут массивную доску так, что она образует наклонную плоскость, один конец которой находится на земле, а другой на грузовике, и по этой плоскости втаскивают ящик. Чтобы поднять ящик вертикально вверх нужно приложить к нему силу, равную его весу ( P ). Перемещая равномерно ящик по наклонной плоскости, в отсутствие трения прикладывают силу, равную ( F=Psinalpha ), т.е. меньшую веса ящика, но при этом, выигрывая в силе, проигрывают в расстоянии. Работа по подъёму ящика по вертикали равна работе, совершаемой при его перемещении вдоль наклонной плоскости. Это справедливо, если сила сопротивления движению пренебрежимо мала. При наличии трения перемещение ящика вдоль наклонной плоскости требует совершения большей работы, чем при его движении вертикально вверх. В этом случае говорят о коэффициенте полезного действия (КПД) наклонной плоскости. Он равен отношению полезной работы ко всей совершённой работе: ( mathbf{КПД}=A_п/A_сcdot 100 % ), где ( A_п ) — полезная работа, ( A_п=mgh ); ( A_с ) — совершённая работа при перемещении ящика вдоль наклонной плоскости, ( A_c=Fl ), где ( F ) — приложенная сила, ( l ) — длина наклонной плоскости.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Исследуя условия равновесия рычага, ученик выполнил соответствующую лабораторную работу. В таблице представлены значения сил и их плеч для рычага, находящегося в равновесии. Определите, чему равно плечо ( l_1 )?
1) 12,8 м
2) 2,5 м
3) 0,8 м
4) 0,25 м
2. Ученик выполнял лабораторную работу по исследованию условий равновесия рычага. Результаты для сил и их плеч, которые он получил, представлены в таблице.
Чему равна сила ( F_1 ), если рычаг находится в равновесии?
1) 100 Н
2) 50 Н
3) 25 Н
4) 9 Н
3. Рычаг находится в равновесии под действием двух сил. Сила ( F_1 ) = 6 Н. Чему равна сила ( F_2 ), если длина рычага 50 см, а плечо силы ( F_1 ) равно 30 см?
1) 0,1 Н
2) 3,6 Н
3) 9 Н
4) 12 Н
4. Выигрыш в силе, приложенной к грузу, нельзя получить с помощью
1) подвижного блока
2) неподвижного блока
3) рычага
4) наклонной плоскости
5. С помощью неподвижного блока в отсутствие трения силе
1) выигрывают в 2 раза
2) не выигрывают, но и не проигрывают
3) проигрывают в 2 раза
4) возможен и выигрыш, и проигрыш
6. С помощью подвижного блока в отсутствие трения
1) выигрывают в работе в 2 раза
2) проигрывают в силе в 2 раза
3) не выигрывают в силе
4) выигрывают в силе в 2 раза
7. На рисунке изображён неподвижный блок, с помощью которого, прикладывая к свободному концу нити силу 20 Н, равномерно поднимают груз. Если трением пренебречь, то масса поднимаемого груза равна
1) 4 кг
2) 2 кг
3) 0,5 кг
4) 1 кг
8. Наклонная плоскость даёт выигрыш в силе в 2 раза. В работе при отсутствии силы трения эта плоскость
1) даёт выигрыш в 2 раза
2) даёт выигрыш в 4 раза
3) не даёт ни выигрыша, ни проигрыша
4) даёт проигрыш в 2 раза
9. Вдоль наклонной плоскости длиной 5 м поднимают груз массой 40 кг, прикладывая силу 160 Н. Чему равна высота наклонной плоскости, если трение при движении груза пренебрежимо мало?
1) 1,25 м
2) 2 м
3) 12,5 м
4) 20 м
10. Груз массой 10 кг поднимают по наклонной плоскости длиной 2 м и высотой 0,5 м, прикладывая силу 40 Н. Чему равен КПД наклонной плоскости?
1) 160%
2) 62,5%
3) 16%
4) 6,25%
11. Груз поднимают с помощью подвижного блока радиусом ( R ) (см. рисунок). Установите соответствие между физическими величинами (левый столбец) и формулами, по которым они определяются (правый столбец).
Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) плечо силы ( vec{F}_1 ) относительно точки A
Б) плечо силы ( vec{F}_2 ) относительно точки A
B) момент силы ( vec{F}_1 ) относительно точки A
ФОРМУЛЫ
1) ( F_1R )
2) ( 2F_1R )
3) ( frac{F_1}{R} )
4) ( R )
5) ( 2R )
12. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.
1) Любой простой механизм даёт выигрыш в силе.
2) Ни один простой механизм не даёт выигрыша в работе.
3) Наклонная плоскость выигрыша в силе не даёт.
4) Коэффициент полезного действия показывает, какая часть совершенной работы является полезной.
5) Неподвижный блок даёт выигрыш в силе в 2 раза.
Часть 2
13. Чему равна сила, с которой действуют на брусок массой 0,2 кг, перемещая его по наклонной плоскости длиной 1,6 м и высотой 0,4 м, если КПД наклонной плоскости 80%.
Ответы
Простые механизмы. КПД простых механизмов
Оценка
Источник
Трактовка понятия
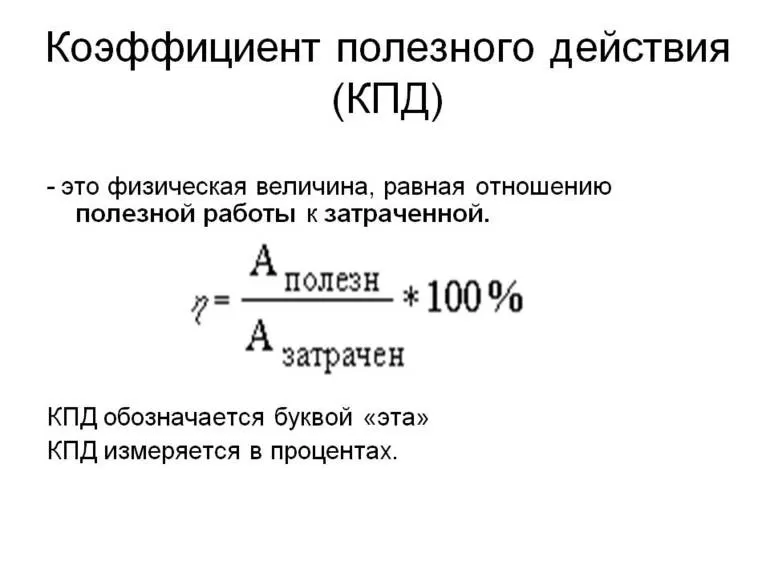
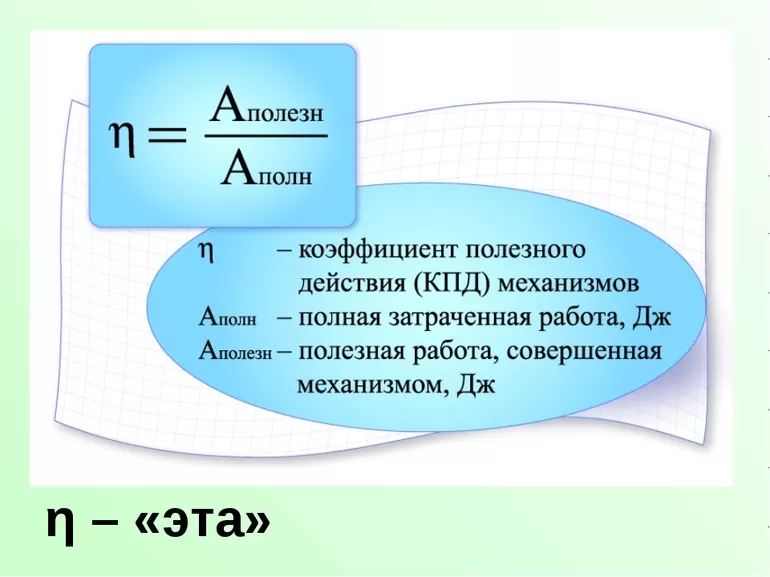
Электродвигатель и другие механизмы выполняют определённую работу, которая называется полезной. Устройство, функционируя, частично растрачивает энергию. Для определения эффективности работы применяется формула ɳ= А1/А2×100%, где:
- А1 — полезная работу, которую выполняет машина либо мотор;
- А2 — общий цикл работы;
- η – обозначение КПД.
Показатель измеряется в процентах. Для нахождения коэффициента в математике используется следующая формула: η= А/Q, где А — энергия либо полезная работа, а Q — затраченная энергия. Чтобы выразить значение в процентах, КПД умножается на 100%. Действие не несёт содержательного смысла, так как 100% = 1. Для источника тока КПД меньше единицы.
В старших классах ученики решают задачи, в которых нужно найти КПД тепловых двигателей. Понятие трактуется следующим образом: отношение выполненной работы силового агрегата к энергии, полученной от нагревателя. Расчет производится по следующей формуле: η= (Q1-Q2)/Q1, где:
- Q1 — теплота, полученная от нагревательного элемента;
- Q2 — теплота, отданная холодильной установке.

Максимальное значение показателя характерно для циклической машины. Она оперирует при заданных температурах нагревательного элемента (Т1) и холодильника (Т2). Измерение осуществляется по формуле: η= (Т1-Т2)/Т1. Чтобы узнать КПД котла, который функционирует на органическом топливе, используется низшая теплота сгорания.
Плюс теплового насоса как нагревательного прибора заключается в возможности получать больше энергии, чем он может затратить на функционирование. Показатель трансформации вычисляется путём деления тепла конденсации на работу, затрачиваемую на выполнение данного процесса.
Мощность разных устройств
По статистике, во время работы прибора теряется до 25% энергии. При функционировании двигателя внутреннего сгорания топливо сгорает частично. Небольшой процент вылетает в выхлопную трубу. При запуске бензиновый мотор греет себя и составные элементы. На потерю уходит до 35% от общей мощности.
При движении механизмов происходит трение. Для его ослабления используется смазка. Но она неспособна полностью устранить явление, поэтому затрачивается до 20% энергии. Пример на автомобиле: если расход составляет 10 литров топлива на 100 км, на движение потребуется 2 л, а остаток, равный 8 л — потеря.
Если сравнивать КПД бензинового и дизельного моторов, полезная мощность первого механизма равна 25%, а второго — 40%. Агрегаты схожи между собой, но у них разные виды смесеобразования:

- Поршни бензинового мотора функционируют на высоких температурах, поэтому нуждаются в хорошем охлаждении. Тепло, которое могло бы перейти в механическую энергию, тратится впустую, что способствует снижению КПД.
- В цепи дизельного устройства топливо воспламеняется в процессе сжатия. На основе данного фактора можно сделать вывод, что давление в цилиндрах высокое, при этом мотор экологичнее и меньше первого аналога. Если проверить КПД при низком функционировании и большом объёме, результат превысит 50%.
Асинхронные механизмы
Расшифровка термина «асинхронность» — несовпадение по времени. Понятие используется во многих современных машинах, которые являются электрическими и способны преобразовывать соответствующую энергию в механическую. Плюсы устройств:
- простое изготовление;
- низкая цена;
- надёжность;
- незначительные эксплуатационные затраты.
Чтобы рассчитать КПД, используется уравнение η = P2 / P1. Для расчёта Р1 и Р2 применяются общие данные потери энергии в обмотках мотора. У большинства агрегатов показатель находится в пределах 80−90%. Для быстрого расчёта используется онлайн-ресурс либо личный калькулятор. Для проверки возможного КПД у мотора внешнего сгорания, который функционирует от разных источников тепла, используется силовой агрегат Стирлинга. Он представлен в виде тепловой машины с рабочим телом в виде жидкости либо газа. Вещество движется по замкнутому объёму.
Принцип его функционирования основан на постепенном нагреве и охлаждении объекта за счёт извлечения энергии из давления. Подобный механизм применяется на косметическом аппарате и современной подводной лодке. Его работоспособность наблюдается при любой температуре. Он не нуждается в дополнительной системе для запуска. Его КПД возможно расширить до 70%, в отличие от стандартного мотора.
Значения показателя

В 1824 году инженер Карно дал определение КПД идеального двигателя, когда коэффициент равен 100%. Для трактовки понятия была создана специальная машина со следующей формулой: η=(T1 — Т2)/ T1. Для расчёта максимального показателя применяется уравнение КПД макс = (T1-T2)/T1x100%. В двух примерах T1 указывает на температуру нагревателя, а T2 — температуру холодильника.
На практике для достижения 100% коэффициента потребуется приравнять температуру охладителя к нулю. Подобное явление невозможно, так как T1 выше температуры воздуха. Процедура повышения КПД источника тока либо силового агрегата считается важной технической задачей. Теоретически проблема решается путём снижения трения элементов двигателя и уменьшения теплопотери. В дизельном моторе подобное достигается турбонаддувом. В таком случае КПД возрастает до 50%.
Мощность стандартного двигателя увеличивается следующими способами:
- подключение к системе многоцилиндрового агрегата;
- применение специального топлива;
- замена некоторых деталей;
- перенос места сжигания бензина.

КПД зависит от типа и конструкции мотора. Современные учёные утверждают, что будущее за электродвигателями. На практике работа, которую совершает любое устройство, превышает полезную, так как определённая её часть выполняется против трения. Если используется подвижный блок, совершается дополнительная работа: поднимается блок с верёвкой, преодолеваются силы трения в блоке.
Решение примеров
Задача 1. Поезд на скорости 54 км/ч развивает мощность 720 кВт. Нужно вычислить силу тяги силовых агрегатов. Решение: чтобы найти мощность, используется формула N=F x v. Если перевести скорость в единицу СИ, получится 15 м/с. Подставив данные в уравнение, определяется, что F равно 48 kН.
Задача 2. Масса транспортного средства соответствует 2200 кг. Машина, поднимаясь в гору под уклоном в 0,018, проходит расстояние 100 м. Скорость развивается до 32,4 км/ч, а коэффициент трения соответствует 0,04. Нужно определить среднюю мощность авто при движении. Решение: вычисляется средняя скорость — v/2. Чтобы определить силу тяги мотора, выполняется рисунок, на котором отображаются силы, воздействующие на машину:
- тяжесть — mg;
- реакция опоры — N;
- трение — Ftr;
- тяга — F.

Первая величина вычисляется по второму закону Ньютона: mg+N+Ftr+F=ma. Для ускорения используется уравнение a=v2/2S. Если подставить последние значение и воспользоваться cos, получится средняя мощность. Так как ускорение считается постоянной величиной и равно 9,8 м/с2, поэтому v= 9 м/с. Подставив данные в первую формулу, получится: N= 9,5 kBt.
При решении сложных задач по физике рекомендуется проверить соответствие предоставленных в условиях единиц измерения с международными стандартами. Если они отличаются, необходимости перевести данные с учётом СИ.
Источник
