Коэффициент полезного действия некоторого двигателя 320

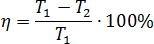
22 ноября 2011

Рассмотрим очередные 8 задач B12 из ЕГЭ по математике. Здесь встречаются 2 темы: температура прибора и КПД теплового двигателя. Для разнообразия часть задач, в которых встречаются квадратные уравнения, будем решать через дискриминант (см. урок «Решение квадратных уравнений»), а часть — через формулы Виета (см. урок «Теорема Виета»).

Задача. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получении экспериментально и на исследуемом интервале температур дается выражением T(t) = T0 + at + bt2,где T0 = 340 K,a = 28 К/мин,b = −0,2 К/мин. Известно, что при температурах нагревателя свыше 1000 К прибор может испортиться, поэтому его надо отключать. Определите (в минутах), через какое наибольшее время после начала работы надо отключать прибор.

Все вертится вокруг температуры, которая меняется по закону: T(t) = T0 + at + bt2. Требуется выяснить, в какой момент эта температура пересечет отметку в 1000 К. Поскольку температура T0, а также коэффициенты a и b нам известны, составим и решим уравнение:

1000 = 340 + 28t − 0,2t2;
0,2t2 −28t + 660 = 0 — перенесли все слагаемые влево;
t2 − 140t + 3300 = 0 — умножили обе стороны на 5.

Дискриминант: D = 1402 − 4 · 1 · 3300 = 6400 = 64 · 100. Очевидно, что корень из дискриминанта равен 80. Корни квадратного уравнения:
t1 = (140 + 80) : 2 = 110;
t2 = (140 − 80) : 2 = 30.

Получается, что у нас есть два кандидата на ответ: числа 110 и 30. Требуется найти наибольшее время, и поэтому многие выбирают ответ 110.

Но давайте вспомним, что означают эти числа. Итак, в момент времени t = 30 минут, а также в момент времени t = 110 минут температура пересекает критическую отметку в 1000 К — ту самую, после которой прибор может испортиться. Грубо говоря, прибор испортится через 30 минут и через 110.

Вывод: прибор надо отключить уже через 30 минут, поскольку к 110 минутам он будет давно испорчен.

Задача. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получении экспериментально и на исследуемом интервале температур дается выражением T(t) = T0 + at + bt2, где T0 = 520 K,a = 22 К/мин,b = −0,2 К/мин. Известно, что при температурах нагревателя свыше 1000 К прибор может испортиться, поэтому его надо отключать. Определите (в минутах), через какое наибольшее время после начала работы надо отключать прибор.

Задача полностью аналогична предыдущей — только коэффициенты другие. Предельно допустимую температуру мы знаем, поэтому составим и решим уравнение:

1000 = 520 + 22t − 0,2t2;
0,2t2 − 22t + 480 = 0 — собрали все слева;
t2 − 110t + 2400 = 0 — умножили обе стороны на 5.

Задача свелась к приведенному квадратному уравнению. По теореме Виета:
t1 + t2 = −(−110) = 110;
t1 · t2 = 2400.

Очевидно, корни: 80 и 30, т.к. 80 + 30 = 110;80 · 30 = 2400. Получаем, что предельная температура будет достигнута через 30 минут и через 80. Следовательно, прибор надо отключить уже через 30 минут.

Задача. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получении экспериментально и на исследуемом интервале температур дается выражением T(t) = T0 + at + bt2, где T0 = 800 K,a = 52 К/мин,b = −0,4 К/мин. Известно, что при температурах нагревателя свыше 2000 К прибор может испортиться, поэтому его надо отключать. Определите (в минутах), через какое наибольшее время после начала работы надо отключать прибор.

Задача аналогична предыдущей, поэтому рассмотрим краткое решение. Именно такой объем вычислений будет достаточным обоснованием ответа в настоящем ЕГЭ по математике.

2000 = 800 + 52t − 0,4t2;
0,4t2 − 52t + 1200 = 0;
t2 − 130t + 3000 = 0 — разделили все на коэффициент 0,4.

Решаем через дискриминант: D = 1302 − 4 · 1 · 3000 = 4900. Корень из дискриминанта: 70. Найдем корни уравнения:
t1 = (130 + 70) : 2 = 100;
t2 = (130 − 70) : 2 = 30.

Из двух чисел выбираем наименьшее — это снова число 30.

Задача. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получении экспериментально и на исследуемом интервале температур дается выражением T(t) = T0 + at + bt2, где T0 = 280 K,a = 26 К/мин,b = −0,2 К/мин. Известно, что при температурах нагревателя свыше 1000 К прибор может испортиться, поэтому его надо отключать. Определите (в минутах), через какое наибольшее время после начала работы надо отключать прибор.

Все так же − составляем и решаем уравнение:

1000 = 280 + 26t − 0,2t2;
0,2t2 − 26t + 720 = 0 — перенесли все слагаемые в одну сторону;
t2 − 130t + 3600 = 0 — умножили каждое слагаемое на 5.

Это приведенное квадратное уравнение, которое хорошо решается по теореме Виета:
t1 + t2 = −(−130) = 130 = 90 + 40;
t1 · t2 = 3600 = 90 · 40.

Из приведенных формул очевидно, что корни: 90 и 40. Как и прежде, придется выбрать наименьшей корень — число 40. Потому что до 90 минут прибор уже «не доживет».

Задача. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получении экспериментально и на исследуемом интервале температур дается выражением T(t) = T0 + at + bt2, где T0 = 1100 K,a = 36 К/мин,b = −0,2 К/мин. Известно, что при температурах нагревателя свыше 2000 К прибор может испортиться, поэтому его надо отключать. Определите (в минутах), через какое наибольшее время после начала работы надо отключать прибор.

Снова задача-клон, которая сводится к уравнению:

2000 = 1100 + 36t − 0,2t2;
0,2t2 − 36t + 900 = 0;
t2 − 180t + 4500 = 0.

Перед нами снова приведенное уравнение. По теореме Виета:
t1 + t2 = −(−180) = 180 = 150 + 30;
t1 · t2 = 4500 = 150 · 30.

Теперь корни очевидны — это числа 150 и 30. В ответ пойдет наименьшее число, т.е. прибор надо выключить через 30 минут.

Задача. Коэффициент полезного действия некоторого двигателя определяется формулой:

При каком минимальном значении температуры нагревателя T1 КПД этого двигателя будет не меньше 60%, если температура холодильника T2 = 200? Ответ дайте в градусах Кельвина.

Для начала упростим исходную формулу. Умножим обе стороны равенства на переменную T1, получим:
η · T1 = (T1 − T2) · 100.

Знак процентов мы специально убрали, поскольку в конечном уравнении никаких процентов не может быть — есть только числа. По условию задачи, нам известны КПД η = 60% и температура холодильника T1 = 200. Подставим эти числа в формулу — получим уравнение:
60 · T1 = (T1 − 200) · 100.

Обратите внимание: единицы измерения снова не пишутся. Никаких процентов, никаких градусов Кельвина — только обычные числа. В принципе, аналогично следует поступать во всех задачах B12. Просто до сих пор мы не акцентировали внимание на этом моменте, но с процентами надо работать аккуратно.

Итак, решаем уравнение:
60 · T1 = (T1 − 200) · 100;
60T1 = 100T1 − 20 000 — раскрыли скобки;
60T1 − 100T1 = −20 000 — собрали все слагаемые с T1 слева;
−40T1 = −20 000;
T1 = 500 — разделили все на −40.

Как видим, задача свелась к простому линейному уравнению, которое имеет один корень. Это очень хорошо, поскольку, в отличие от квадратных уравнений, здесь не придется размышлять, какой из корней записать в ответ.

Задача. Коэффициент полезного действия некоторого двигателя определяется формулой:

При каком минимальном значении температуры нагревателя T1 КПД этого двигателя будет не меньше 60%, если температура холодильника T2 = 400? Ответ дайте в градусах Кельвина.

Задача полностью аналогична предыдущей. Преобразуем исходную формулу, а затем подставим в нее известные переменные:

η · T1 = (T1 − T2) · 100 — преобразовали формулу;
60 · T1 = (T1 − 400) · 100 — подставили числа;
60T1 − 100T1 = −40 000 — группируем слагаемые, содержащие переменную T1;
−40T1 = −40 000;
T1 = 1000 — разделили обе стороны на коэффициент −40.

Задача. Коэффициент полезного действия некоторого двигателя определяется формулой:

При каком минимальном значении температуры нагревателя T1 КПД этого двигателя будет больше 80%, если температура холодильника T2 = 100? Ответ дайте в градусах Кельвина.

Еще одна задача-клон. Приведу лишь краткое решение:

η · T1 = (T1 − T2) · 100 — преобразованная формула;
80 · T1 = (T1 − 100) · 100 — подставили числа;
80T1 − 100T1 = −10 000;
−20T1 = −10 000;
T1 = 500 — это и есть ответ.

Смотрите также:

1. Упрощаем решение задач с помощью замены переменной
2. Решение задач B12: №440—447
3. Метод Гаусса
4. Следствия из теоремы Виета
5. Пробный ЕГЭ по математике 2015: 4 вариант
6. Тест по задачам B14: легкий уровень, 1 вариант