Коэффициент полезного действия если температура холодильника 275

6.3. Второй закон термодинамики

6.3.1. Коэффициент полезного действия тепловых двигателей. Цикл Карно

Второе начало термодинамики возникло из анализа работы тепловых двигателей (машин). В формулировке Кельвина оно выглядит следующим образом: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.

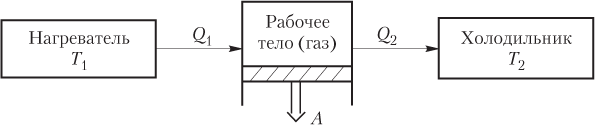
Схема действия тепловой машины (теплового двигателя) представлена на рис. 6.3.

Рис. 6.3

Цикл работы теплового двигателя состоит из трех этапов:

1) нагреватель передает газу количество теплоты Q
1;

2) газ, расширяясь, совершает работу A;

3) для возвращения газа в исходное состояние холодильнику передается теплота Q
2.

Из первого закона термодинамики для циклического процесса

Q = A,

где Q — количество теплоты, полученное газом за цикл, Q = Q
1 − Q
2; Q
1 — количество теплоты, переданное газу от нагревателя; Q
2 — количество теплоты, отданное газом холодильнику.

Поэтому для идеальной тепловой машины справедливо равенство

Q
1 − Q
2 = A.

Когда потери энергии (за счет трения и рассеяния ее в окружающую среду) отсутствуют, при работе тепловых машин выполняется закон сохранения энергии

Q
1 = A + Q
2,

где Q
1 — теплота, переданная от нагревателя рабочему телу (газу); A — работа, совершенная газом; Q
2 — теплота, переданная газом холодильнику.

Коэффициент полезного действия тепловой машины вычисляется по одной из формул:

η=AQ1⋅100 %, η=Q1−Q2Q1⋅100 %, η=(1−Q2Q1)⋅100 %,

где A — работа, совершенная газом; Q
1 — теплота, переданная от нагревателя рабочему телу (газу); Q
2 — теплота, переданная газом холодильнику.

Наиболее часто в тепловых машинах используется цикл Карно, так как он является самым экономичным.

Цикл Карно состоит из двух изотерм и двух адиабат, показанных на рис. 6.4.

Рис. 6.4

Участок 1–2 соответствует контакту рабочего вещества (газа) с нагревателем. При этом нагреватель передает газу теплоту Q
1 и происходит изотермическое расширение газа при температуре нагревателя T
1. Газ совершает положительную работу (A
12 > 0), его внутренняя энергия не изменяется (∆U
12 = 0).

Участок 2–3 соответствует адиабатному расширению газа. При этом теплообмена с внешней средой не происходит, совершаемая положительная работа A
23
приводит к уменьшению внутренней энергии газа: ∆U
23
= −A
23
, газ охлаждается до температуры холодильника T
2.

Участок 3–4 соответствует контакту рабочего вещества (газа) с холодильником. При этом холодильнику от газа поступает теплота Q
2 и происходит изотермическое сжатие газа при температуре холодильника T
2. Газ совершает отрицательную работу (A
34 < 0), его внутренняя энергия не изменяется (∆U
34 = 0).

Участок 4–1 соответствует адиабатному сжатию газа. При этом теплообмена с внешней средой не происходит, совершаемая отрицательная работа A
41
приводит к увеличению внутренней энергии газа: ∆U
41
= −A
41
, газ нагревается до температуры нагревателя T
1, т.е. возвращается в исходное состояние.

Коэффициент полезного действия тепловой машины, работающей по циклу Карно, вычисляется по одной из формул:

η=T1−T2T1⋅100 %, η=(1−T2T1)⋅100 %,

где T
1 — температура нагревателя; T
2 — температура холодильника.

Пример 9. Идеальная тепловая машина совершает за цикл работу 400 Дж. Какое количество теплоты передается при этом холодильнику, если коэффициент полезного действия машины равен 40 %?

Решение. Коэффициент полезного действия тепловой машины определяется формулой

η=AQ1⋅100 %,

где A — работа, совершаемая газом за цикл; Q
1 — количество теплоты, которое передается от нагревателя рабочему телу (газу).

Искомой величиной является количество теплоты Q
2, переданное от рабочего тела (газа) холодильнику, не входящее в записанную формулу.

Связь между работой A, теплотой Q
1, переданной от нагревателя газу, и искомой величиной Q
2 устанавливается с помощью закона сохранения энергии для идеальной тепловой машины

Q
1 = A + Q
2.

Уравнения образуют систему

η=AQ1⋅100 %,Q1=A+Q2,}

которую необходимо решить относительно Q
2.

Для этого исключим из системы Q
1, выразив из каждого уравнения

Q1=Aη⋅100 %,Q1=A+Q2}

и записав равенство правых частей полученных выражений:

Aη⋅100 %=A+Q2.

Искомая величина определяется равенством

Q2=Aη⋅100 %−A=A(100 %η−1).

Расчет дает значение:

Q2=400⋅(100 %40 %−1)=600 Дж.

Количество теплоты, переданной за цикл от газа холодильнику идеальной тепловой машины, составляет 600 Дж.

Пример 10. В идеальной тепловой машине от нагревателя к газу поступает 122 кДж/мин, а от газа холодильнику передается 30,5 кДж/мин. Вычислить коэффициент полезного действия данной идеальной тепловой машины.

Решение. Для расчета коэффициента полезного действия воспользуемся формулой

η=(1−Q2Q1)⋅100 %,

где Q
2 — количество теплоты, которое передается за цикл от газа холодильнику; Q
1 — количество теплоты, которое передается за цикл от нагревателя рабочему телу (газу).

Преобразуем формулу, выполнив деление числителя и знаменателя дроби на время t:

η=(1−Q2/tQ1/t)⋅100 %,

где Q
2/t — скорость передачи теплоты от газа холодильнику (количество теплоты, которое передается газом холодильнику в секунду); Q
1/t — скорость передачи теплоты от нагревателя рабочему телу (количество теплоты, которое передается от нагревателя газу в секунду).

В условии задачи скорость передачи теплоты задана в джоулях в минуту; переведем ее в джоули в секунду:

• от нагревателя газу —

Q1t=122 кДж/мин=122⋅10360 Дж/с;

• от газа холодильнику —

Q2t=30,5 кДж/мин=30,5⋅10360 Дж/с.

Рассчитаем коэффициент полезного действия данной идеальной тепловой машины:

η=(1−30,5⋅10360⋅60122⋅103)⋅100 %=75 %.

Пример 11. Коэффициент полезного действия тепловой машины, работающей по циклу Карно, равен 25 %. Во сколько раз увеличится коэффициент полезного действия, если температуру нагревателя увеличить, а температуру холодильника уменьшить на 20 %?

Решение. Коэффициент полезного действия идеальной тепловой машины, работающей по циклу Карно, определяется следующими формулами:

• до изменения температур нагревателя и холодильника —

η1=(1−T2T1)⋅100 %,

где T
1 — первоначальная температура нагревателя; T
2 — первоначальная температура холодильника;

• после изменения температур нагревателя и холодильника —

η2=(1−T′2T′1)⋅100 %,

где T′1 — новая температура нагревателя, T′1=1,2T1; T′2 — новая температура холодильника, T′2=0,8T2.

Уравнения для коэффициентов полезного действия образуют систему

η1=(1−T2T1)⋅100 %,η2=(1−0,8T21,2T1)⋅100 %,}

которую необходимо решить относительно η2.

Из первого уравнения системы с учетом значения η1 = 25 % найдем отношение температур

T2T1=1−η1100 %=1−25 %100 %=0,75

и подставим во второе уравнение

η2=(1−0,81,2⋅0,75)⋅100 %=50 %.

Искомое отношение коэффициентов полезного действия равно:

η2η1=50 %25 %=2,0.

Следовательно, указанное изменение температур нагревателя и холодильника тепловой машины приведет к увеличению коэффициента полезного действия в 2 раза.