Коэффициент полезного действия двигателя постоянного тока
Дата публикации: 23 января 2013.
Категория: Машины постоянного тока.
Общие положения
Коэффициент полезного действия определяется как отношение полезной, или отдаваемой, мощности P2 к потребляемой мощности P1:
| (1) |
или в процентах
| (2) |
Современные электрические машины имеют высокий коэффициент полезного действия (к. п. д.). Так, у машин постоянного тока мощностью 10 кВт к. п. д. составляет 83 – 87%, мощностью 100 кВт – 88 – 93% и мощностью 1000 кВт – 92 – 96%. Лишь малые машины имеют относительно низкие к. п. д.; например, у двигателя постоянного тока мощностью 10 Вт к. п. д. 30 – 40%.
 |
| Рисунок 1. Зависимость коэффициента полезного действия электрической машины от нагрузки |
Кривая к. п. д. электрической машины η = f(P2) сначала быстро растет с увеличением нагрузки, затем к. п. д. достигает максимального значения (обычно при нагрузке, близкой к номинальной) и при больших нагрузках уменьшается (рисунок 1). Последнее объясняется тем, что отдельные виды потерь (электрические Iа2rа и добавочные) растут быстрее, чем полезная мощность.
Прямой и косвенный методы определения коэффициента полезного действия
Прямой метод определения к. п. д. по экспериментальным значениям P1 и P2 согласно формуле (1) может дать существенную неточность, поскольку, во-первых, P1 и P2 являются близкими по значению и, во-вторых, их экспериментальное определение связано с погрешностями. Наибольшие трудности и погрешности вызывает измерение механической мощности.
Если, например, истинные значения мощности P1 = 1000 кВт и P2 = 950 кВт могут быть определены с точностью 2%, то вместо истинного значения к. п. д.
η = 950/1000 = 0,95
можно получить
или
Поэтому ГОСТ 25941-83, “Машины электрические вращающиеся. Методы определения потерь и коэффициента полезного действия”, предписывает для машин с η% ≥ 85% косвенный метод определения к. п. д., при котором по экспериментальным данным определяется сумма потерь pΣ.
Подставив в формулу (1) P2 = P1 – pΣ, получим
| (3) |
Применив здесь подстановку P1 = P2 + pΣ, получим другой вид формулы:
| (4) |
Так как более удобно и точно можно измерять электрические мощности (для двигателей P1 и для генераторов P2), то для двигателей более подходящей является формула (3) и для генераторов формула (4). Методы экспериментального определения отдельных потерь и суммы потерь pΣ описываются в стандартах на электрические машины и в руководствах по испытанию и исследованию электрических машин. Если даже pΣ определяется со значительно меньшей точностью, чем P1 или P2, при использовании вместо выражения (1) формул (3) и (4) получаются все же значительно более точные результаты.
Условия максимума коэффициента полезного действия
Различные виды потерь различным образом зависят от нагрузки. Обычно можно считать, что одни виды потерь остаются постоянными при изменении нагрузки, а другие являются переменными. Например, если генератор постоянного тока работает с постоянной скоростью вращения и постоянным потоком возбуждения, то механические и магнитные потери являются также постоянными. Наоборот, электрические потери в обмотках якоря, добавочных полюсов и компенсационной изменяются пропорционально Iа², а в щеточных контактах – пропорционально Iа. Напряжение генератора при этом также приблизительно постоянно, и поэтому с определенной степенью точности P2 ∼ Iа.
Таким образом, в общем, несколько идеализированном случае можно положить, что
или
где коэффициент нагрузки
Kнг = I / Iн = P2 / P2н | (6) |
Определяет относительную величину нагрузки машины.
Суммарные потери также можно выразить через kнг:
pΣ = p0 + kнг × p1 + kнг² × p2, | (7) |
где p0 – постоянные потери, не зависящие от нагрузки; p1 – значение потерь, зависящих от первой степени kнг при номинальной нагрузке; p2 – значение потерь, зависящих от квадрата kнг, при номинальной нагрузке.
Подставим P2 из (5) и pΣ из (7) в формулу к. п. д.
Тогда
| (8) |
Установим, при каком значении kнг к. п. д. достигает максимального значения, для чего определим производную dη/dkнг по формуле (8) и приравняем ее к нулю:
Это уравнение удовлетворяется, когда его знаменатель равен бесконечности, т. е. при kнг = ∞. Этот случай не представляет интереса. Поэтому необходимо положить равным нулю числитель. При этом получим
Таким образом, к. п. д. будет максимальным при такой нагрузке, при которой переменные потери kнг² × p2, зависящие от квадрата нагрузки, становятся равными постоянным потерям p0.
Значение коэффициента нагрузки при максимуме к. п. д., согласно формуле (9),
| (10) |
Если машина проектируется для заданного значения ηмакс, то, поскольку потери kнг × p1 обычно относительно малы, можно считать, что
p0 + p2 ≈ pΣ = const.
Изменяя при этом соотношение потерь p0 и p2, можно достичь максимального значения к. п. д. при различных нагрузках. Если машина работает большей частью при нагрузках, близких к номинальной, то выгодно, чтобы значение kнг [смотрите формулу (10)] было близко к единице. Если машина работает в основном при малых нагрузках, то выгодно, чтобы значение kнг [смотрите формулу (10)] было соответственно меньше.
Источник: Вольдек А. И., “Электрические машины. Учебник для технических учебных заведений” – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.
Источник
Коэффициент полезного действия является важнейшим показателем двигателей постоянного тока. Чем он больше, тем меньше мощность Р и ток I, потребляемые двигателем из сети при одной и той же механической мощности. В общем виде зависимостьть такова:
(9)

где – потери в обмотке якоря; – потери в обмотке возбуждения; – потери в магнитопроводе якоря; – механические потери.
Потери мощности не зависят, и мало зависят от нагрузки двигателя.
Двигатели рассчитываются таким образом, чтобы максимальное значение КПД было в области, близкой к номинальной мощности. Эксплуатация двигателей при малых нагрузках нежелательна вследствие малых значений rя. Значения КПД двигателей с различными способами возбуждения и мощностью от 1 до 100 кВт при номинальной нагрузке разные и составляют в среднем 0,8.
Рабочие характеристики
Рабочими называются регулировочная, скоростная, моментная и к.п.д. характеристики.
Регулировочная характеристика
Регулировочная характеристика представляет зависимость скорости вращения П от тока Iв возбуждения в случае, если ток Iа якоря и напряжение U сети остаются неизменными, т. е. n=f(Iв) при Ia=const и U=const.
До тех пор, пока сталь магнитопривода машины не насыщена, поток Ф изменяется пропорционально току возбуждения Iв. В этом случае регулировочная характеристика является гиперболической. По мере насыщения при больших токах Iв характеристика приближается к линейной (рис. 2). При малых значениях тока Iв скорость вращения резко возрастает. Поэтому при обрыве цепи возбуждения двигателя (Iв = 0) с параллельным возбуждением скорость его вращения достигает недопустимых пределов, как говорят: «Двигатель идет вразнос». Исключение могут составлять микродвигатели, которые имеют относительно большой момент М0 холостого хода.

Рис. 2. Регулировочная характеристика двигателя
В двигателях последовательного возбуждения Iв = Iа. При малых нагрузках ток якоря Iа мал и скорость вращения может быть слишком большой, поэтому пуск и работа при малых нагрузках недопустимы. Микродвигатели так же, как и. в предыдущем случае, могут составлять исключение.
Скоростные характеристики.
Скоростные характеристики дают зависимость скорости вращения п от полезной мощности Р2 на валу двигателя в случае, если напряжение U сети и сопротивление rв регулировочного реостата цепи возбуждения остаются неизменными, т. е. n=f(P2), при U=const и rв = const.

Рис. 3. Скоростные характеристики
С возрастанием тока якоря при увеличении механической нагрузки двигателя параллельного возбуждения одновременно увеличивается падения напряжения в якоре и появляется реакция якоря, которая обычно действует размагничивающим образом. Первая причина стремится уменьшить скорость вращения двигателя, вторая — увеличить. Действие падения напряжения в якоре обычно оказывает большее влияние. Поэтому скоростная характеристика двигателя параллельного возбуждения имеет слегка падающий характер (кривая 1, рис. 3).
В двигателе последовательного возбуждения ток якоря является током возбуждения. В результате скоростная характеристика двигателя с последовательным возбуждением имеет характер, близкий к гиперболическому. При увеличении нагрузки по мере насыщения магнитной цепи характеристика приобретает более прямолинейный характер (кривая 3 на рис. 3).
В компаундном двигателе при согласном включении обмоток скоростная характеристика занимает промежуточное положение между характеристиками двигателя параллельного и последовательного возбуждения (кривая 2).
Моментные характеристики.
Моментные характеристики показывают, как изменяется момент М при изменении полезной мощности Р2 на валу двигателя, если напряжение U сети и сопротивление rв регулировочного реостата в цепи возбуждения остаются неизменными, т. е. М = f(P2), при U=const, rв=const.
Полезный момент на валу двигателя

Если скорость вращения двигателя параллельного возбуждения не изменялась бы с нагрузкой, то зависимость момента Ммех от полезной мощности графически представляла бы прямую линию, проходящую через начало координат. В действительности скорость вращения с увеличением нагрузки падает. Поэтому характеристика полезного момента несколько загибается кверху (кривая 2, рис. 4). При этом кривая электромагнитного момента М проходит выше кривой полезного момента Ммех на постоянную величину, равную моменту холостого хода М0 (кривая 1).

Рис. 4. Моментные характеристики
В двигателе последовательного возбуждения вид моментной характеристики приближается к параболическому, так как изменение момента от тока нагрузки происходит, по закону параболы, пока сталь не насыщена. По мере насыщения зависимость приобретает более прямолинейный характер (кривая 4). В компаундном двигателе моментная характеристика (кривая 3) занимает промежуточное положение между характеристиками двигателя параллельного и последовательного возбуждения.
Характеристика изменения коэффициента полезного действия.
Кривая зависимости к. п. д. от нагрузки имеет характерный для всех двигателей вид (рис 5). Кривая проходит через начало координат и быстро растет при увеличении полезной мощности до 1/4 номинальной. При мощности Р2, равной примерно 2/3 номинальной, к. п. д. обычно достигает максимального значения. При увеличении нагрузки до номинальной к. п. д. остается постоянным или незначительно падает.

Рис. 5. Изменение к. п. д. двигателя
Источник
Электрическими двигателями переменного или постоянного тока комплектуются приводы станков, насосов и вентиляторов, а также других механизмов, используемых на предприятиях тяжелой и легкой промышленности. Рентабельность производства напрямую зависит от себестоимости продукции, на которую в большой степени влияет эффективность эксплуатации оборудования, поэтому КПД и мощность электродвигателя являются основными параметрами, на основании которых выполняется подбор привода.
Определение КПД электродвигателя
Принцип работы любой электрической машины основан на преобразовании энергии тока, протекающего по обмоткам статора и создающего магнитное поле, во вращение ротора. Коэффициент полезного действия (КПД) электродвигателя определяется соотношением вырабатываемой им механической мощности на валу (p2) к полной мощности, потребляемой из сети (p1) и выражается в процентах:
η=p2/p1*100%
 Исходя из формулы, следует, что чем ближе этот параметр к единице, тем выше будет эффективность использования оборудования.
Исходя из формулы, следует, что чем ближе этот параметр к единице, тем выше будет эффективность использования оборудования.
Факторы, влияющие на величину КПД
Коэффициент полезного действия никогда не может быть равным единице, так как существуют неизбежные потери, снижающие полезную мощность. Они делятся на три группы:
- электрические;
- магнитные;
- механические.
Электрические потери зависят от степени нагрузки двигателя и являются следствием нагрева обмоток статора, вызванного работой тока по преодолению электрического сопротивления проводников, из которых они выполнены. Поэтому максимальный КПД электродвигателя достигается, когда нагрузка на двигатель составляет 75% от максимальной расчетной величины.
Магнитные потери происходят из-за неизбежного перемагничивания активного железа статора и ротора, а также возникновения в нем вихревых токов.
Третья группа обусловлена наличием трения в подшипниках, на которых вращается вал, а также сопротивлением, оказываемым воздухом крыльчатке вентилятора и самому ротору (якорю). Из-за наличия щеточно-коллекторного узла КПД электродвигателя постоянного тока несколько ниже коэффициента полезного действия машин с короткозамкнутым ротором. Это также относится к асинхронным электродвигателям с фазным ротором из-за дополнительного трения щеток об контактные кольца.
Способы повысить КПД двигателя
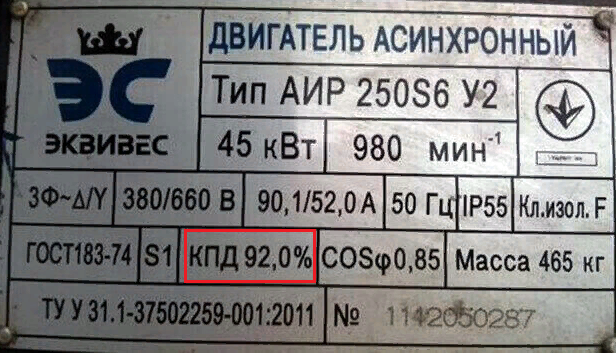
Следует помнить, что реальный коэффициент полезного действия может несколько отличатся от паспортных величин, указанных на шильдике двигателя. Чтобы выполнить расчет КПД электродвигателя в реальных условиях эксплуатации, необходимо учитывать неравномерность распределения питающего напряжения в фазах. В зависимости от величины асимметрии падение полезной мощности может достигать 5-7%.
Увеличение КПД электрической машины возможно только за счет снижения потерь и контроля качества силовой сети.
Механические потери можно уменьшить благодаря более качественным подшипникам, установки крыльчатки вентилятора, выполненной из современных материалов для уменьшения сопротивлению воздуху. Нагрев обмоток можно уменьшить благодаря использованию обмоточных проводов, выполненных из очищенной меди, имеющих меньшее сопротивление.
Снизить потери на перемагничивание активного железа и минимизировать влияние вихревых токов можно используя для набора сердечника необходимо использовать качественную электромагнитную сталь с надежной изоляцией. Кроме того, ведутся работы по разработке наилучшей геометрии зубцов статора, благодаря которым будет увеличена концентрация магнитного поля.
В реальности КПД асинхронного электродвигателя можно несколько увеличить за счет использования частотного преобразователя, позволяющего оптимизировать расход электроэнергии. Следует помнить, что эффективность эксплуатации двигателя с КПД 98% сильно упадет, если его использовать для приведения в движения механизма, имеющего более низкий коэффициент полезного действия.
Источник
Коэффициентом полезного действия называется отношение полезной мощности Р2 к потребляемой мощности
????2
Р1 ???? = (140). Для современных машин постоянного тока КПД находится в пределах:
????1
1) Мощность больше 10 кВт – 83-87%;
2) Мощность более 100 кВт – 88-93%;
3) Более 1000 кВт – 92-96%;
4) И только у электрических машин малой мощности этот показатель очень низкий, например, электрическая машина мощность 10 Вт, ее КПД 30-40%.
Зависимость КПД от нагрузки представлена на (рис. 4.74 методичка).
В режиме холостого хода КПД машины постоянного тока равен нулю. Нет полезной мощности Р2=0. При увеличении нагрузки КПД резко возрастает, что связано с небольшой величиной переменных потерь и практически неизменными постоянными потерями. При некоторой нагрузке КПД достигает максимального значения. Дальнейшее повышение нагрузки приводит к снижению КПД, что связано со значительным увеличением переменных потерь, которые пропорциональны нагрузке в квадрате. Но при этом, полезная мощность растет медленнее чем переменные потери, так как полезная мощность пропорциональна нагрузке в первой степени.
Существуют два способа определения КПД:
1) Прямой;
2) Косвенный;
В машинах постоянного тока, как и в других электрических машинах, прямой способ не применяют, так как величины Р2 и Р1 по своим значениям близки друг к другу. А это значит, есть вероятность неверного определения КПД. Поэтому для машин постоянного тока применяют косвенный метод, заключающийся в том, что определяют потери в машине (суммарные потери). И на основании их определяют КПД. Однако КПД определяют по формулам
∑????
???? = 1 − L 66scM+tH/qBhGyslJRwyNFDH2GVah7Imh2HmO2LxDr53GOXsK217HKXctfo+SRbaYcOyUGNH65rK 4/bkDLyNOK4e0pdhczysz9+7+fvXJiVjbm+m1TOoSFO8hOEXX9ChEKa9P7ENqjUgj8Q/FW+eLEDt JfMIusj1f/TiBwAA//8DAFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAA AAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAA AAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAMSyF3l6AgAAUwYAAA4AAAAA AAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAJFJqfDZAAAAAgEAAA8A AAAAAAAAAAAAAAAA1AQAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAADaBQAAAAA= “> , для ГПТ
????н+∑????
???? , для ДПТ
????1
(141).
Когда машина постоянного тока работает двигателем, то более точнее можно определить потребляемую мощность по электрическим величинам: напряжению и току. Для генератора отдаваемую мощность так же более точнее определять через электрические величины напряжения и тока. В машинах постоянного тока есть два вида потерь:
1) Постоянные потери;
2) Переменные потери;
Постоянные потери — это потери, которые не зависят от нагрузки, их обозначим через Ро. Переменные потери состоят из двух составляющих: потери которые пропорциональны нагрузке в первой степени, обозначим через Р1. Вторую составляющую переменный потерь обозначим через Р2, которые пропорциональны квадрату нагрузки.
???? ???? ????
Тогда можно записать ???? (142), определим значение КПД при такой нагрузке, когда
этот КПД достигает максимального значения. Для этого рассмотрим в качестве примера генератор постоянного тока с независимым возбуждением. Для такого генератора будем считать, что выходное напряжение U остается неизменным, тогда для такого генератора полезная мощность будет равна ????2 =
????????
????н???????? = ????н????н ????н = ????2нКнг (143).
????????
Кнг = ????н (144) называется коэффициентом нагрузки, относительная доля некоторой нагрузки по отношению к номинальной.
В свете рассуждений запишем выражение для КПД: ???? = К нгР +????Кнг+КР2нР +К2 ????2 (145).
2н 0 нг 1 нг
LECTION #14
Возьмем КПД по коэффициенту нагрузки, исходя из выражения для КПД получим
???? ????????Кнг = КнгР2????н2+н(????????0+????−ККнг2нгР1????+2)К2нг????2 (146). Полученное выражение приравняем к нулю. Данное уравнение
удовлетворяется, если знаменатель равен бесконечности. То есть, коэффициент нагрузки равен также бесконечности.
Однако, это условие не представляет интереса. Приравняем числитель данного выражения к нулю
????2Н(Р0 − К2нг????2) = 0, ????0 = К2нг????2(147). Условие определяющее максимальное значение КПД. То есть, КПД в машине постоянного тока достигает максимального значения при условии, что постоянные потери равны переменным потерям, что видно на (рис. 4.74 методичка).
Режим генератора
Рассмотрим процесс преобразования энергии в машинах постоянного тока для генераторного режима на примере генератора постоянного тока с постоянным возбуждением, который приводится во вращение с помощью приводного двигателя с установившимся режимом работы при n=const.
Это преобразование проиллюстрируем с помощью энергетической диаграммы.
Если при независимом возбуждении возбудитель, который питает обмотку возбуждения и находится на одном валу с генератором постоянного тока, то мощность возбуждения не учитывается в мощность, которая подводится к валу этого генератора. Если это так, то тогда эта мощность не учитывается.
Часть мощности Р1 (механической мощности), которая поступает на вал генератора, идет на покрытие механических потерь в генераторе. Другая часть этой мощности идет на покрытие магнитных потерь в сталь генератора. Оставшееся мощность — это электромагнитная мощность, которую можно определить через электрические величины генератора, либо с помощью энергетической диаграммы Рэм = Еа???????? = ????1 − (????мех +
Рмг) (148).
Часть этой мощности (электромагнитной) расходуется на покрытие электрических потерь в обмотке якоря, в которую входят все потери обмоток, которые включены последовательно с обмоткой якоря. Другая часть этой мощности идет на компенсацию потерь на переходном сопротивлении определяемой щетками. Эти составляющие можно рассчитать
Рэла = ????????2???????? Рщ = ∆????щ????????(149).
Возникающие при работе генератора добавочные потери особо не учитываются. Частично не включают магнитные потери в стали одну часть, а другую часть в электрические потери обмотки якоря. Тогда полезную мощность можно рассчитать через электрические величины
????2 = ???????????? = ????эм − (Рэла + Рщ) = Рэм − (????????2???????? + ∆????щ????????) (150).
Электромагнитная мощность — это мощность которая связывает подводимую механическую мощность к валу генератора и полезную мощность, которая отдается потребителю. Режим двигателя
Рассмотрим процесс преобразования энергии для двигательного режима на примере двигателя постоянного тока, работающего в установившемся режиме при неизменной частоте вращения n=const. Рассмотрим этот вопрос на примере двигателя постоянного тока с параллельным возбуждением.
Из сети двигатель постоянного тока потребляет электрическую мощность Р1
????1 = ????????н = ????(???????? +????????) (151).
Часть этой мощности расходуется на компенсацию электрических потерь в обмотке возбуждение. Другая часть этой мощности идет на покрытие электрических потерь в обмотке якоря. Еще одна часть этой мощности идет на покрытие потерь, имеющих место на щетках.
Каждую из этих составляющих потерь определяются по формулам какие свойственны для генератора постоянного тока.
Оставшееся мощность — это электромагнитная мощность, которую можно рассчитать
Рэм = Рмех = Еа???????? = ????1 − (∆???????? + Рэла + Рщ) = ????(???????? + ????????) − ???????????? − ????????2???????? + ∆????щ ???????? (152). Эта электромагнитная мощность в свою очередь преобразуется в механическую мощность. Эти мощности можно рассчитать на основании энергетической диаграммы.
Тогда Рэм = Рмех = ???????????? − (????????2???????? + ∆????щ????????) (153) полезная мощность двигателя постоянного тока определяется следующим образом: часть электромагнитной мощности идет на компенсацию магнитных потерь в стали двигателя. Другая часть этой мощности идет на компенсацию механических потерь в двигателе. Оставшаяся мощность — это полезная мощность Р2, которая поступает с вала двигателя на вал рабочего механизма. С учетом энергетической диаграммы полезную мощность можно определить ????2 = ????эм − (Рмг + Рмех) (154). Так как сумма магнитных и механических потерь — это потери холостого хода (постоянные потери), то полезную мощность можно рассчитать по соответствующей формуле
Р2 = Рэм − Р0(155).
Источник
