Как зависит полезная мощность от силы тока в цепи
ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ:
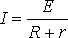 , (1)
, (1)
I- сила тока в цепи; Е- электродвижущая сила источника тока, включённого в цепь; R- сопротивление внешней цепи; r- внутреннее сопротивление источника тока.
МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО ВНЕШНЕЙ ЦЕПИ
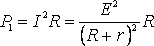 . (2)
. (2)
Из формулы (2) видно, что при коротком замыкании цепи (R®0) и при R®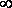 эта мощность равна нулю. При всех других конечных значениях Rмощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R0, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
эта мощность равна нулю. При всех других конечных значениях Rмощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R0, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
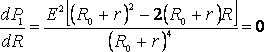 . (3)
. (3)
Из формулы (3), с учётом того, что R и r всегда положительны, а Е ? 0, после несложных алгебраических преобразований получим:
R0 = r. (4)
Следовательно, мощность, выделяемая во внешней цепи, достигает наибольшего значения при сопротивлении внешней цепи равном внутреннему сопротивлению источника тока.
При этом сила тока в цепи 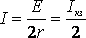 (5)
(5)
равна половине тока короткого замыкания. При этом мощность, выделяемая во внешней цепи, достигает своего максимального значения, равного
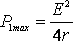 . (6)
. (6)
Когда источник замкнут на внешнее сопротивление, то ток протекает и внутри источника и при этом на внутреннем сопротивлении источника выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла равна
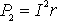 .
.  (7)
(7)
Следовательно, полная мощность, выделяемая во всей цепи , определится формулой
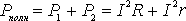 = I2(R+r) = IE (8)
= I2(R+r) = IE (8)
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ источника тока равен 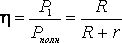 . (9)
. (9)
Из формулы (8) следует, что
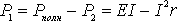 , (10)
, (10)
т.е. Р1 изменяется с изменением силы тока в цепи по параболическому закону и принимает нулевые значения при I = 0 и при 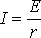 . Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид
. Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид
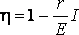 (11)
(11)
Таким образом, к.п.д. достигает наибольшего значения h =1 в случае разомкнутой цепи ( I = 0), а затем уменьшается по линейному закону, обращаясь в нуль при коротком замыкании.
Зависимость мощностей Р1, Рполн = EI и к.п.д. источника тока от силы тока в цепи показаны на рис.1.


Рис.1. I0 E/r
Из графиков видно, что получить одновременно полезную мощность и к.п.д. невозможно. Когда мощность, выделяемая на внешнем участке цепи Р1, достигает наибольшего значения, к.п.д. в этот момент равен 50%.
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ

Рис. 2.
Соберите на экране цепь, показанную на рис. 2. Для этого сначала щелкните левой кнопкой мыши над кнопкой  э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.
э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.
Разместите далее последовательно с источником резистор, изображающий его внутреннее сопротивление (нажав предварительно кнопку  в нижней части экрана) и амперметр (кнопка
в нижней части экрана) и амперметр (кнопка  там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр
там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр  , измеряющий напряжение на нагрузке.
, измеряющий напряжение на нагрузке.
Подключите соединительные провода. Для этого нажмите кнопку провода  внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.
внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.
4. Установите значения параметров для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой  . Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
. Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
Таблица 1. Исходные параметры электрической цепи
Номер варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Е, В | 10,0 | 9,5 | 9,0 | 8,5 | 8,0 | 8,5 | 9,0 | 9,5 |
r, Ом | 4,8 | 5,7 | 6,6 | 7,5 | 6,4 | 7,3 | 8,2 | 9,1 |
5. Установите сопротивление внешней цепи 2 Ом, нажмите кнопку «Счёт» и запишите показания электроизмерительных приборов в соответствующие строки таблицы 2.
6. Последовательно увеличивайте с помощью движка регулятора сопротивление внешней цепи на 0,5 Ом от 2 Ом до 20 Ом и, нажимая кнопку «Счёт», записывайте показания электроизмерительных приборов в таблицу 2.
7. Вычислите по формулам (2), (7), (8), (9) Р1, Р2, Рполн и h для каждой пары показаний вольтметра и амперметра и запишите рассчитанные значения в табл.2.
8. Постройте на одном листе миллиметровой бумаге графики зависимости P1 = f(R), P2 = f(R), Pполн=f(R), h = f (R) и U = f(R).
9. Рассчитайте погрешности измерений и сделайте выводы по результатам проведённых опытов.
Таблица 2. Результаты измерений и расчётов
R, Ом | 2,0 | 2,5 | 3,0 | … | 20 |
U, В | |||||
I, А | |||||
P1, Вт | |||||
P2, ВТ | |||||
Pполн, ВТ | |||||
h |
Вопросы и задания для самоконтроля
- Запишите закон Джоуля-Ленца в интегральной и дифференциальной формах.
- Что такое ток короткого замыкания?
- Что такое полная мощность?
- Как вычисляется к.п.д. источника тока?
- Докажите, что наибольшая полезная мощность выделяется при равенстве внешнего и внутреннего сопротивлений цепи.
- Верно ли утверждение, что мощность, выделяемая во внутренней части цепи, постоянна для данного источника?
- К зажимам батарейки карманного фонаря присоединили вольтметр, который показал 3,5 В.
- Затем вольтметр отсоединили и на его место подключили лампу, на цоколе которой было написано: Р=30 Вт, U=3,5 В. Лампа не горела.
- Объясните явление.
- При поочерёдном замыкании аккумулятора на сопротивления R1 и R2 в них за одно и то же время выделилось равное количество тепла. Определите внутреннее сопротивление аккумулятора.
Источник
Рассмотрим
электрическую цепь, состоящую из
источника постоянного тока и внешнего
сопротивления R
(рис. 1). При протекании тока через
такую цепь источником ЭДС выполняется
работа и в цепи выделяется мощность.
П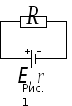 олезной
олезной
мощностью называют
мощность, которая выделяется на внешнем
сопротивлении. Из закона Джоуля-Ленца
(10*) полезная
мощность равняется
![]() ,
,
а из закона Ома для участка цепи![]() .
.
Тогда полезная мощность будет
| (1) |
где
![]() – падение напряжения на внешнем
– падение напряжения на внешнем
сопротивлении. При протекании тока по
цепи также выделяется „бесполезная”
мощность – разогревается источник ЭДС.
По закону Джоуля-Ленца эта мощность
равняется![]() .
.
Полная мощность, которая выделяется во
всей цепи, равняется![]() .
.
Используя закон Ома для полной цепи![]() ,
,
можно найти полную мощность
| (2) |
И так,
так,
полная мощность, которая выделяется в
цепи, равняется произведению силы тока
на ЭДС источника тока.
Пусть
в цепи можно менять внешнее сопротивление
![]() .
.
Проанализируем, как полезная и полная
мощности зависят от силы тока и внешнего
сопротивления.
Полезная
мощность
равняется разности между полной мощностью
и „бесполезной”:
| (3) |
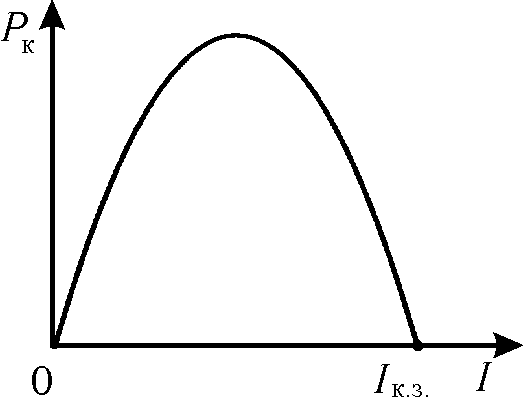
![]()

Рис. 2
Из этого
выражения видно, что полезная мощность
является квадратичной функцией силы
тока I.
График этой функции будет представлять
собой параболу (рис. 2).
Из рис. 2
вытекает, что
![]() в двух случаях:
в двух случаях:
когда
цепь разомкнута (R = ∞),
то сила тока в цепи I = 0;когда
возникло короткое заключение, при этом
R = 0,
а сила тока в цепи будет максимальной
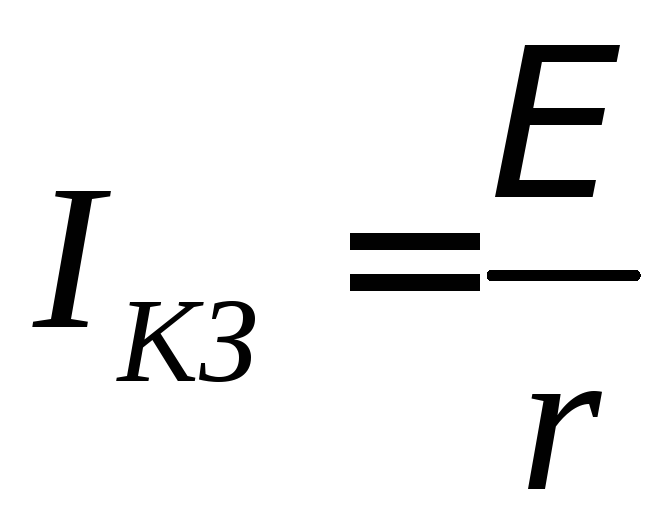 .
.
Меняя
величину внешнего сопротивления, можно
достичь некоторого значения силы тока
в цепи, при котором полезная мощность
будет максимальной. Найдем этот ток.
Для этого найдем первую производную
![]() и приравняем ее нулю. Из выражения (3)
и приравняем ее нулю. Из выражения (3)
имеем:
| (4) |
Отсюда
вытекает
| (5) |
а ток
![]() ,
,
при котором выделяется максимальная
полезная мощность, равняется![]() .
.
С другой стороны, на основании закона
Ома для полной цепи![]() ,
,
где![]() – сопротивление, при котором выделяется
– сопротивление, при котором выделяется
максимальная полезная мощность.
Приравнивая два последних выражения![]() ,
,
находим, что
| (6) |
Таким
образом, полезная
мощность будет максимальной при условии
равенства внешнего и внутреннего
сопротивлений.
Зависимость
полезной мощности от внешнего сопротивления
можно найти из закона
Джоуля-Ленца
![]() и закона Ома для полной цепи
и закона Ома для полной цепи![]()
| (7) |
График
зависимости
![]() показан на рис. 3 (криваяб).
показан на рис. 3 (криваяб).
Максимум функции
![]() можно найти, приравнивая
можно найти, приравнивая![]() нулю
нулю
| (8) |
Из
(8) также вытекает ожидаемое равенство
![]() .
.
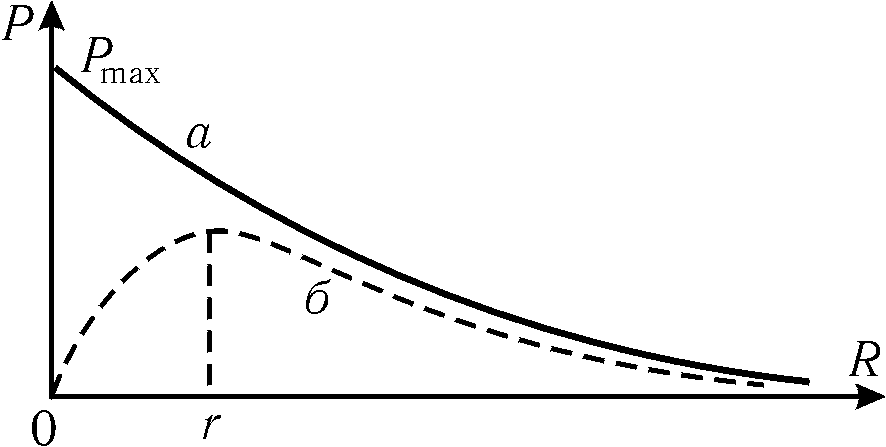

а
– полная мощность
б
– корисна потужність
Рис.
3
Рассмотрим
теперь, как полная мощность
зависит от внешнего сопротивления.
Используя выражение (2) и закон Ома для
полной цепи
![]() находим зависимость полной мощности
находим зависимость полной мощности
от внешнего сопротивления:
![]() .
.
(9)
График этой
зависимости показана на рис. 3 (кривая
а). При
изменении внешнего сопротивления от
нуля (короткое заключение) до бесконечности
(цепь разомкнута) полная мощность будет
убывать от максимального значения
![]() до нуля.
до нуля.
Зависимость
коэффициента полезного действия
источника электрического тока от силы
тока и внешнего сопротивления цепи
К оэффициент
оэффициент
полезного действия
(КПД) равняется отношению полезной
мощности (1) к полной мощности (2), которая
выделяется во всей цепи
| (10) |
С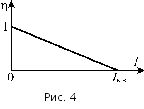 начала
начала
найдем зависимость КПД
от силы тока. Если
разделить выражение (3) для полезной
мощности на выражение (1) для полной
мощности, получим
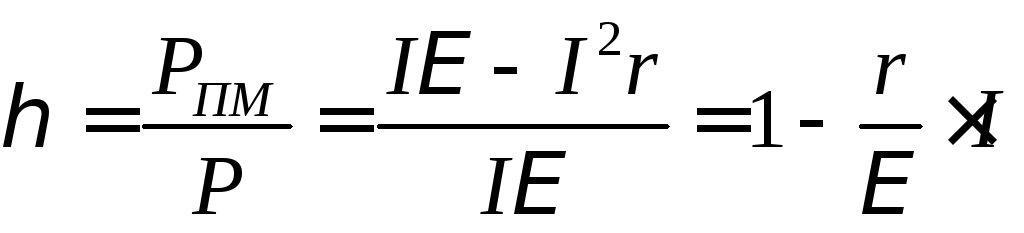
(11)
И так,
так,
КПД представляет собой линейную функцию
от силы тока (рис. 4). Когда I → 0
(цепь разомкнут), то
![]() .
.
При коротком заключении![]() ,
,
ток короткого заключения
| (12) |
и
КПД будет
![]() .
.
Чтобы найти
зависимость КПД от
внешнего сопротивления,
подставим в (9) выражение для
![]() из закона Ома для участки цепи
из закона Ома для участки цепи![]() ,
,
а выражение для![]() – из закона Ома для полной цепи
– из закона Ома для полной цепи![]() .
.
Тогда
| (13) |
Из соотношения (13)
вытекает:
при
R® 0
(короткое заключение,
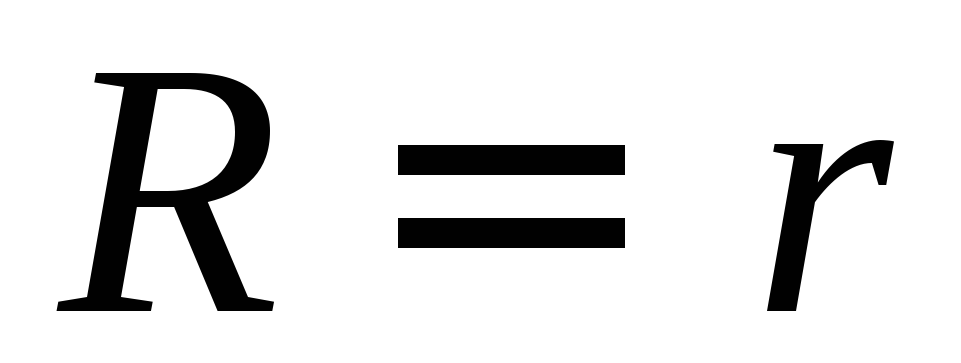 )
) ;
;при
R® ¥
( цепь разомкнут,
 )
) ;
;при
R = r
(условие максимума полезной мощности)
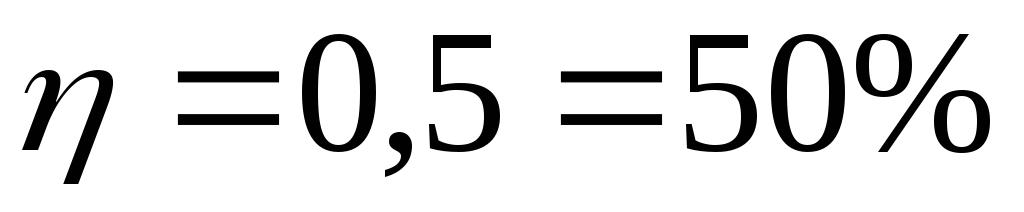 .
.
Приведенный
анализ показывает, что при увеличении
внешнего сопротивления КПД асимптотично
приближается к единице (рис. 5).
Соседние файлы в папке doc-формат
- #
- #
- #
- #
- #
- #
Источник
 Первое упоминание об электричестве встречается в опытах древнегреческого философа Фалеса. Именно он первым обнаружил, что предметы при трении притягиваются. Одноименный термин был введен в начале 17-го века английским физиком Гилбертом, после опытов, проведенных с магнитами. Отцом же науки об электричестве считается французский ученый Кулон – именно после открытия закона, получившего его имя, электротехника начала свою победную поступь, которая продолжается до сих пор. Этот закон утверждает, что два точечных заряда в безвоздушной среде взаимодействуют с силой, прямо пропорциональной их модулям и обратно – расстоянию между ними, возведенному в квадрат.
Первое упоминание об электричестве встречается в опытах древнегреческого философа Фалеса. Именно он первым обнаружил, что предметы при трении притягиваются. Одноименный термин был введен в начале 17-го века английским физиком Гилбертом, после опытов, проведенных с магнитами. Отцом же науки об электричестве считается французский ученый Кулон – именно после открытия закона, получившего его имя, электротехника начала свою победную поступь, которая продолжается до сих пор. Этот закон утверждает, что два точечных заряда в безвоздушной среде взаимодействуют с силой, прямо пропорциональной их модулям и обратно – расстоянию между ними, возведенному в квадрат.
Выясним, что же представляет собой понятие электричество?
Если коротко, то это – направленное движение потока заряженных частиц. Тела, через которые они проходят, называются проводниками. Каждый проводник имеет определенное сопротивление электрическому току, которое раз
И, перед тем, как перейти к основным законам, несколько слов о заряженных частицах: они бывают, условно говоря, положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные – притягиваются.
А теперь, перейдем к главному.
Основа-основ науки об электричестве – закон Ома.
Эксперимент, который провел этот немецкий физик, привел его к следующему убеждению: сила тока I, проходящего через металлический проводник, пропорциональна напряжению на его концах, или I = U/R
Здесь напряжением называется разность, образно говоря, «давлений», созданных двумя точками электрической цепи. Измеряют его в вольтах. Электрический ток представляет собой число электронов, которые пропускает участок электрической цепи и измеряется в амперах. Сопротивлением считается свойство цепи помешать этому движению. В честь упомянутого физика, его измеряют в омах. Иначе говоря, проводник, через который проходит ток в 1 ампер при напряжении в 1 вольт, обладает сопротивлением в 1 ом.
Вся остальная электротехника «пляшет» от этого.

О мощности электрического тока
В физике мощностью считают скорость выполнения работы. Неважно, какой. Чем эта операция проводится быстрее, тем большей считается мощность того, кто ее исполняет, будь то человек, механическое устройство или что-то еще.
Так же и в случае с электрическим током: ее мощность представляет собой отношение работы, произведенной движущимися электрическими зарядами к промежутку времени, которое для этого понадобилось.
Проще говоря, для того, чтобы получить электрическую мощность в 1 ватт, когда источник тока имеет напряжение 1 вольт, необходимо пропустить через проводник ток в 1 ампер. Другими словами, мощность (P) можно посчитать, перемножив друг на друга электрическое напряжение и ток:
P = U*I.
Запомнив эту нехитрую формулу, на практике можно рассчитать мощность. Например, если известны значения тока и сопротивления, а о напряжении сведений нет, можем воспользоваться законом Ома, подставив в формулу вместо него I*R. Получится, что мощность равна квадрату электрического тока, помноженному на сопротивление.
Этот закон точно так же придет на помощь, если известны величины напряжения и сопротивления. В этом случае подставив вместо значения тока I = U/R, получим значение мощности, равное квадрату напряжения, поделенному на сопротивление.
Вот так – ничего сложного!
Источник
Мощность, развиваемая источником тока во всей цепи, называется полной мощностью.
Она определяется по формуле
где Pоб-полная мощность, развиваемая источником тока во всей цепи, вт;
Е- э. д. с. источника, в;
I-величина тока в цепи, а.
В общем виде электрическая цепь состоит из внешнего участка (нагрузки) с сопротивлением R и внутреннего участка с сопротивлением R0 (сопротивлением источника тока).
Заменяя в выражении полной мощности величину э. д. с. через напряжения на участках цепи, получим
Величина UI соответствует мощности, развиваемой на внешнем участке цепи (нагрузке), и называется полезной мощностью Pпол=UI.
Величина UoI соответствует мощности, бесполезно расходуемой внутри источника, Ее называют мощностью потерь Po=UoI.
Таким образом, полная мощность равна сумме полезной мощности и мощности потерь Pоб=Pпол+P0.
Отношение полезной мощности к полной мощности, развиваемой источником, называется коэффициентом полезного действия, сокращенно к. п. д.,и обозначается η.
Из определения следует
При любых условиях коэффициент полезного действия η ≤ 1.
Если выразить мощности через величину тока и сопротивления участков цепи, получим
Таким образом, к. п. д. зависит от соотношения между внутренним сопротивлением источника и сопротивлением потребителя.
Обычно электрический к. п. д. принято выражать в процентах.
Для практической электротехники особый интерес представляют два вопроса:
1. Условие получения наибольшей полезной мощности
2. Условие получения наибольшего к. п. д.
Наибольшую полезную мощность( мощность на нагрузке) электрический ток развивает в том случае, если сопротивление нагрузки равно сопротивлению источника тока.
Эта наибольшая мощность равна половине всей мощности (50%) развиваемой источником тока во всей цепи.
Половина мощности развивается на нагрузке и половина развивается на внутреннем сопротивлении источника тока.
Если будем уменьшать сопротивление нагрузки, то мощность развиваемая на нагрузке будет уменьшаться а мощность развиваемая на внутреннем сопротивлении источника тока будет увеличиваться.
Если сопротивление нагрузки равно нулю то ток в цепи будет максимальным, это режим короткого замыкания (КЗ). Почти вся мощность будет развивается на внутреннем сопротивлении источника тока. Этот режим опасен для источника тока а также для всей цепи.
Если сопротивление нагрузки будем увеличивать, то ток в цепи будет уменьшатся, мощность на нагрузке также будет уменьшатся. При очень большом сопротивлении нагрузки тока в цепи вообще не будет. Это сопротивление называется бесконечно большим. Если цепь разомкнута то ее сопротивление бесконечно большое. Такой режим называется режимом холостого хода.
Таким образом, в режимах, близких к короткому замыканию и к холостому ходу, полезная мощность мала в первом случае за счет малой величины напряжения, а во втором за счет малой величины тока.
Коэффициент полезного действия (к. п. д.) равен 100% при холостом ходе ( в этом случае полезная мощность не выделяется, но в то же время и не затрачивается мощность источника).
По мере увеличения тока нагрузки к. п. д. уменьшается по прямолинейному закону.
В режиме короткого замыкания к. п. д. равен нулю ( полезной мощности нет, а мощность развиваемая источником, полностью расходуется внутри него).
Подводя итоги вышеизложенному, можно сделать выводы.
Условие получения максимальной полезной мощности( R=R0) и условие получения максимального к. п. д. (R=∞) не совпадают. Более того, при получении от источника максимальной полезной мощности ( режим согласованной нагрузки) к. п. д.составляет 50%, т.е. половина развиваемой источником мощности бесполезно затрачивается внутри него.
В мощных электрических установках режим согласованной нагрузки является неприемлемым, так как при этом происходит бесполезная затрата больших мощностей. Поэтому для электрических станций и подстанций режимы работы генераторов, трансформаторов, выпрямителей рассчитываются так, чтобы обеспечивался высокий к. п. д. ( 90% и более).
Иначе обстоит дело в технике слабых токов. Возьмем, например, телефонный аппарат. При разговоре перед микрофоном в схеме аппарата создается электрический сигнал мощностью около 2 мвт. Очевидно, что для получения наибольшей дальности связи необходимо передать в линию как можно большую мощность, а для этого требуется выполнить режим согласованного включения нагрузки. Имеет ли в данном случае существенное значение к. п. д.? Конечно нет, так как потери энергии исчисляются долями или единицами милливатт.
Режим согласованной нагрузки применяется в радиоаппаратуре. В том случае, когда согласованный режим при непосредственном соединении генератора и нагрузки не обеспечивается, применяют меры согласования их сопротивлений.
Источник
Мощность, развиваемая источником тока во всей цепи, называется полной мощностью.
Она определяется по формуле
где Pоб-полная мощность, развиваемая источником тока во всей цепи, вт;
Е- э. д. с. источника, в;
I-величина тока в цепи, а.
В общем виде электрическая цепь состоит из внешнего участка (нагрузки) с сопротивлением R и внутреннего участка с сопротивлением R0 (сопротивлением источника тока).
Заменяя в выражении полной мощности величину э. д. с. через напряжения на участках цепи, получим
Величина UI соответствует мощности, развиваемой на внешнем участке цепи (нагрузке), и называется полезной мощностью Pпол=UI.
Величина UoI соответствует мощности, бесполезно расходуемой внутри источника, Ее называют мощностью потерь Po=UoI.
Таким образом, полная мощность равна сумме полезной мощности и мощности потерь Pоб=Pпол+P0.
Отношение полезной мощности к полной мощности, развиваемой источником, называется коэффициентом полезного действия, сокращенно к. п. д.,и обозначается η.
Из определения следует
При любых условиях коэффициент полезного действия η ≤ 1.
Если выразить мощности через величину тока и сопротивления участков цепи, получим
Таким образом, к. п. д. зависит от соотношения между внутренним сопротивлением источника и сопротивлением потребителя.
Обычно электрический к. п. д. принято выражать в процентах.
Для практической электротехники особый интерес представляют два вопроса:
1. Условие получения наибольшей полезной мощности
2. Условие получения наибольшего к. п. д.
Наибольшую полезную мощность( мощность на нагрузке) электрический ток развивает в том случае, если сопротивление нагрузки равно сопротивлению источника тока.
Эта наибольшая мощность равна половине всей мощности (50%) развиваемой источником тока во всей цепи.
Половина мощности развивается на нагрузке и половина развивается на внутреннем сопротивлении источника тока.
Если будем уменьшать сопротивление нагрузки, то мощность развиваемая на нагрузке будет уменьшаться а мощность развиваемая на внутреннем сопротивлении источника тока будет увеличиваться.
Если сопротивление нагрузки равно нулю то ток в цепи будет максимальным, это режим короткого замыкания (КЗ). Почти вся мощность будет развивается на внутреннем сопротивлении источника тока. Этот режим опасен для источника тока а также для всей цепи.
Если сопротивление нагрузки будем увеличивать, то ток в цепи будет уменьшатся, мощность на нагрузке также будет уменьшатся. При очень большом сопротивлении нагрузки тока в цепи вообще не будет. Это сопротивление называется бесконечно большим. Если цепь разомкнута то ее сопротивление бесконечно большое. Такой режим называется режимом холостого хода.
Таким образом, в режимах, близких к короткому замыканию и к холостому ходу, полезная мощность мала в первом случае за счет малой величины напряжения, а во втором за счет малой величины тока.
Коэффициент полезного действия (к. п. д.) равен 100% при холостом ходе ( в этом случае полезная мощность не выделяется, но в то же время и не затрачивается мощность источника).
По мере увеличения тока нагрузки к. п. д. уменьшается по прямолинейному закону.
В режиме короткого замыкания к. п. д. равен нулю ( полезной мощности нет, а мощность развиваемая источником, полностью расходуется внутри него).
Подводя итоги вышеизложенному, можно сделать выводы.
Условие получения максимальной полезной мощности( R=R0) и условие получения максимального к. п. д. (R=∞) не совпадают. Более того, при получении от источника максимальной полезной мощности ( режим согласованной нагрузки) к. п. д.составляет 50%, т.е. половина развиваемой источником мощности бесполезно затрачивается внутри него.
В мощных электрических установках режим согласованной нагрузки является неприемлемым, так как при этом происходит бесполезная затрата больших мощностей. Поэтому для электрических станций и подстанций режимы работы генераторов, трансформаторов, выпрямителей рассчитываются так, чтобы обеспечивался высокий к. п. д. ( 90% и более).
Иначе обстоит дело в технике слабых токов. Возьмем, например, телефонный аппарат. При разговоре перед микрофоном в схеме аппарата создается электрический сигнал мощностью около 2 мвт. Очевидно, что для получения наибольшей дальности связи необходимо передать в линию как можно большую мощность, а для этого требуется выполнить режим согласованного включения нагрузки. Имеет ли в данном случае существенное значение к. п. д.? Конечно нет, так как потери энергии исчисляются долями или единицами милливатт.
Режим согласованной нагрузки применяется в радиоаппаратуре. В том случае, когда согласованный режим при непосредственном соединении генератора и нагрузки не обеспечивается, применяют меры согласования их сопротивлений.
Источник

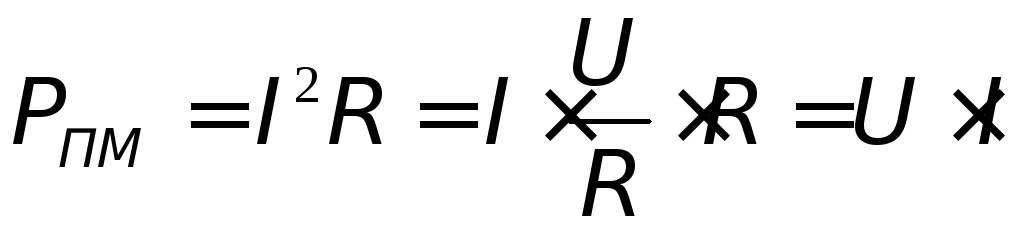 ,
,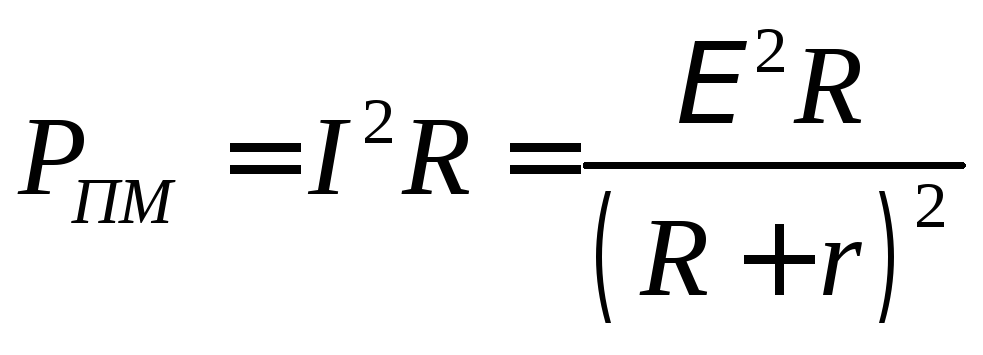 .
.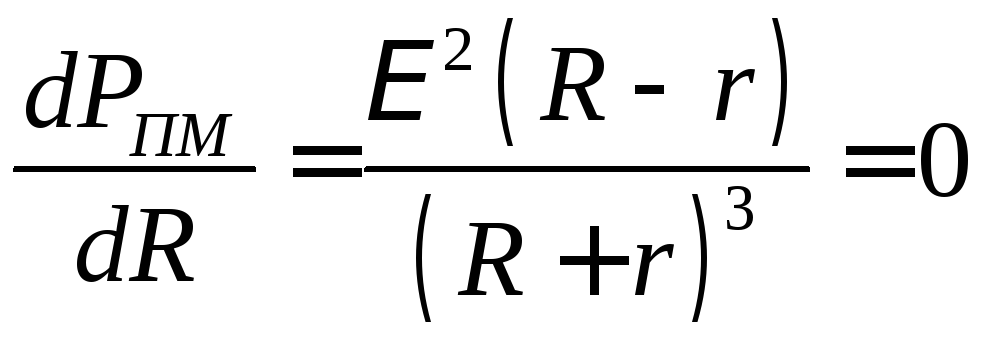 .
.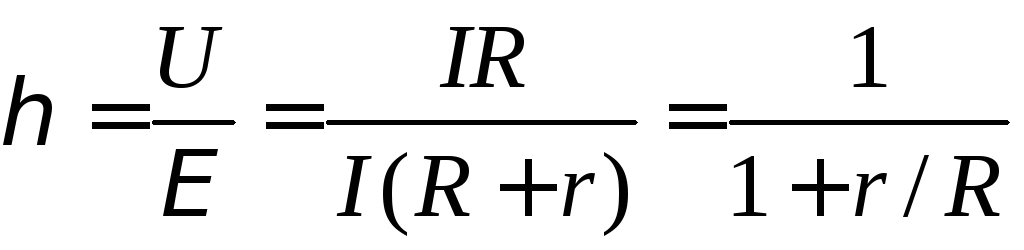 .
.