Как решать задачи по коэффициенту полезного действия
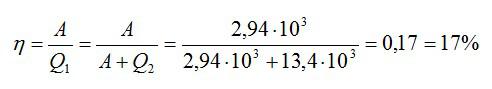
У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.
Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.
Задачи по физике на КПД теплового двигателя
Задача на вычисление КПД теплового двигателя №1
Условие
Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.
Решение
Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:
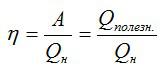
Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:
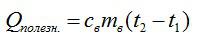
Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.
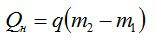
Подставляем значения и вычисляем:
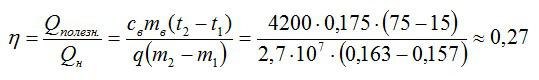
Ответ: 27%
Задача на вычисление КПД теплового двигателя №2
Условие
Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.
Решение
Найдем общее количество теплоты, которое произвел двигатель:
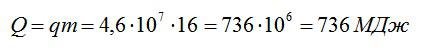
Теперь можно рассчитать КПД:
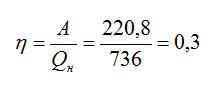
Или, умножая на 100, получаем значение КПД в процентах:
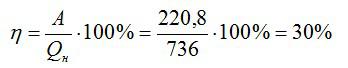
Ответ: 30%.
Задача на вычисление КПД теплового двигателя №3
Условие
Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.
Решение
КПД идеальной тепловой машины:
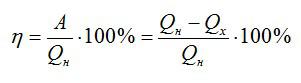
По условию:
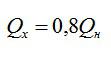
Вычислим сначала работу, а затем КПД:
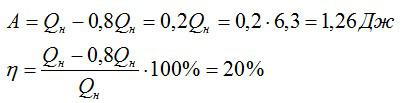
Ответ: 20%; 1,26 Дж.
Задача на вычисление КПД теплового двигателя №4
Условие
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.
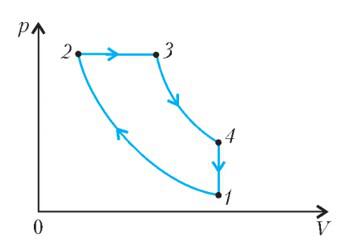
Решение
Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.
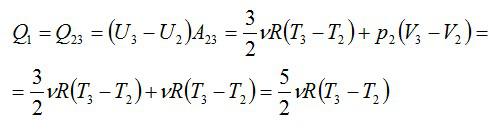
Аналогично:
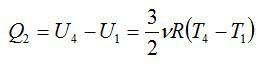
Получим результат:
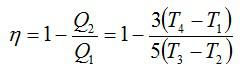
Ответ: См. выше.
Задача на вычисление КПД теплового двигателя №5
Условие
Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.
Решение
Запишем формулу для КПД:
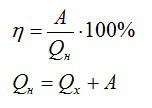
Отсюда:
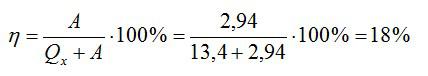
Ответ: 18%
Вопросы на тему тепловые двигатели
Вопрос 1. Что такое тепловой двигатель?
Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.
Вопрос 2. Приведите примеры тепловых двигателей.
Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:
- ракетный двигатель;
- авиационный двигатель;
- газовая турбина.
Вопрос 3. Может ли КПД двигателя быть равен единице?
Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.
КПД реальных двигателей редко превышает 30%.
Вопрос 4. Что такое КПД?
Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.
Вопрос 5. Что такое удельная теплота сгорания топлива?
Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.
Задачи и вопросы на цикл Карно
Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.
Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).
Задача на цикл Карно №1
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.
Решение
Рассчитаем КПД цикла:
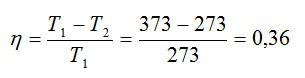
С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:
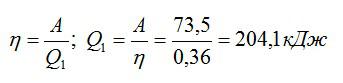
Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:
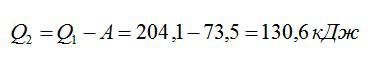
Ответ: 0,36; 204,1 кДж; 130,6 кДж.
Задача на цикл Карно №2
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.
Решение
Формула для КПД цикла Карно:
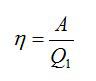
Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:
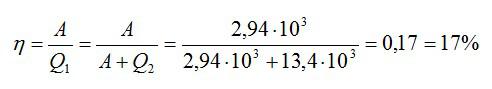
Ответ: 17%.
Задача на цикл Карно №3
Условие
Изобразите цикл Карно на диаграмме и опишите его
Решение
Цикл Карно на диаграмме PV выглядит следующим образом:
- 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
- 2-3. Адиабатическое расширение, тепло не подводится;
- 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
- 4-1. Адиабатическое сжатие.
Ответ: см. выше.
Вопрос на цикл Карно №1
Сформулируйте первую теорему Карно
Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.
Вопрос на цикл Карно №2
Может ли коэффициент полезного действия в цикле Карно быть равным 100%?
Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.
Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.
1. Повторение формул и величин
Данный урок посвящён решению задач. Мы рассмотрим несколько задач на нахождение КПД тепловых установок. Кроме непосредственно КПД, в них фигурируют формулы для количества теплоты, необходимого для нагревания вещества или выделяемого при охлаждении, а также количества теплоты, которое выделяется при сгорании топлива.
Все эти вопросы мы уже рассматривали на прошлых уроках. Однако мы ещё не уделяли отдельное внимание задачам, в которых теплота сгорания топлива идёт на нагревание тел.
Поэтому на этом уроке мы подробно рассмотрим решение задач на нахождение КПД тепловых установок и двигателей. Как мы знаем, любая тепловая установка характеризуется своим КПД. Для нахождения КПД нам могут пригодиться следующие формулы:
– количество теплоты, которое выделяется при сгорании топлива (
– удельная теплота сгорания, 
– масса топлива);
– количество теплоты, которое выделяется при охлаждении или необходимо для нагревания вещества (
– удельная теплоёмкость вещества, 
– масса вещества, 
– конечная температура вещества,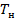 
– начальная температура вещества);
– КПД установки (
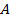– работа, совершённая рабочим телом, 
– количество теплоты, полученное от нагревателя);
Большинство из величин, встречающихся в формулах, либо даны в условии, либо являются искомыми. Однако удельная теплоёмкость вещества и удельная теплота сгорания берутся из соответствующих таблиц. Напомним единицы измерения этих величин: 
.
Кроме этих величин в задачах могут встречаться ещё две табличные величины: 
– удельная теплота парообразования, 
– удельная теплота плавления. Однако на этом уроке они нам не понадобятся, поэтому подробно останавливаться на них не будем.
Для удобства составим таблицу с теми значениями табличных величин, которые понадобятся на этом уроке при решении задач.
cellspacing=”0″>
Вещество | Удельная теплоёмкость | Удельная теплота сгорания |
Вода |
| – |
Спирт |
|
|
Бензин |
|
|
2. Задача №1 на нахождение КПД
На спиртовке нагревают воду. Взяли 
воды и нагрели от 
до 
. При этом масса спиртовки уменьшилась с 
до 
. Найти КПД тепловой установки.
Решение
Запишем краткое условие задачи.
cellspacing=”0″>
Дано: | СИ | Решение: Вначале выпишем формулу для КПД:
В данном случае мы заменили работу полезным количеством теплоты, то есть тем количеством теплоты, которое пошло непосредственно на нагрев воды. |
|
| |
Найти:
|
.
Прежде чем решать задачу, необходимо определиться с процессами, которые происходят в данной задаче. Первый процесс – это сгорание топлива. Второй – нагревание воды.
Полезное количество теплоты, то есть то тепло, которое пошло непосредственно на нагревание воды, можно вычислить по формуле:
Количество теплоты, выделенное нагревателем, то есть, в данном случае, тепло, выделившееся при сгорании спирта:
Массу сгоревшего спирта найти легко: это та масса, на которую уменьшилась масса спиртовки, то есть: 
.
Получаем: 
.
Осталось вычислить КПД установки:
.
Заметим, что КПД может вычисляться не только в процентах, но и в долях. К примеру, для данной задачи ответ может быть: 
.
Если анализировать данную задачу, то можно увидеть, что только четвёртая часть (приблизительно) тепла, которое выделяется при сгорании спирта, идёт на нагревание воды. С одной стороны, это кажется достаточно малым значением, но, с другой стороны, для многих тепловых машин такое значение КПД оказывается даже большим.
Ответ:
.
3. Задача №2 на нахождение КПД
Тепловой двигатель совершил полезную работу 
и израсходовал при этом 
бензина. Найти КПД теплового двигателя.
Решение
Запишем краткое условие задачи.
cellspacing=”0″>
Дано: | СИ | Решение: Вначале выпишем формулу для КПД: |
|
| |
Найти:
|
. По таблице находим, что: 
. Для того чтобы найти КПД, достаточно найти 
Как и в прошлой задаче, воспользуемся следующей формулой: 
.
Находим КПД:
.
Ответ:
.
Итак, мы решили несколько задач на нахождение КПД тепловых двигателей и установок, вспомнили основные формулы и величины, которые требуются для решения таких задач.
На следующем уроке мы рассмотрим более сложные задачи, которые могут встретиться в теме «Тепловые явления».
Вопросы к конспектам
Каков КПД теплового двигателя, который совершил полезную работу 
, если при полном сгорании топлива выделилась бы энергия 
?
Израсходовав 
бензина, тепловой двигатель совершил полезную работу 
. Каков КПД этого двигателя?
Сколько природного газа необходимо сжечь для совершения полезной работы 
, если КПД двигателя 
?
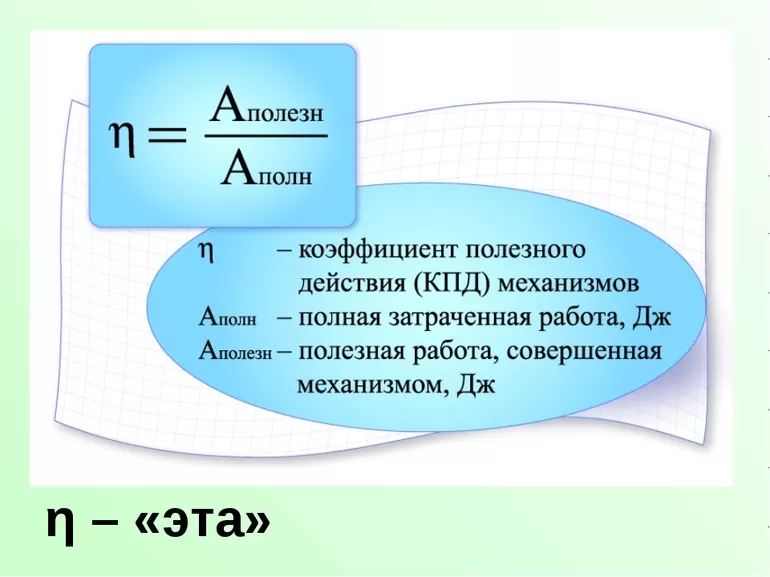
Трактовка понятия
Электродвигатель и другие механизмы выполняют определённую работу, которая называется полезной. Устройство, функционируя, частично растрачивает энергию. Для определения эффективности работы применяется формула ɳ= А1/А2×100%, где:
- А1 — полезная работу, которую выполняет машина либо мотор;
- А2 — общий цикл работы;
- η – обозначение КПД.
Показатель измеряется в процентах. Для нахождения коэффициента в математике используется следующая формула: η= А/Q, где А — энергия либо полезная работа, а Q — затраченная энергия. Чтобы выразить значение в процентах, КПД умножается на 100%. Действие не несёт содержательного смысла, так как 100% = 1. Для источника тока КПД меньше единицы.
В старших классах ученики решают задачи, в которых нужно найти КПД тепловых двигателей. Понятие трактуется следующим образом: отношение выполненной работы силового агрегата к энергии, полученной от нагревателя. Расчет производится по следующей формуле: η= (Q1-Q2)/Q1, где:
- Q1 — теплота, полученная от нагревательного элемента;
- Q2 — теплота, отданная холодильной установке.
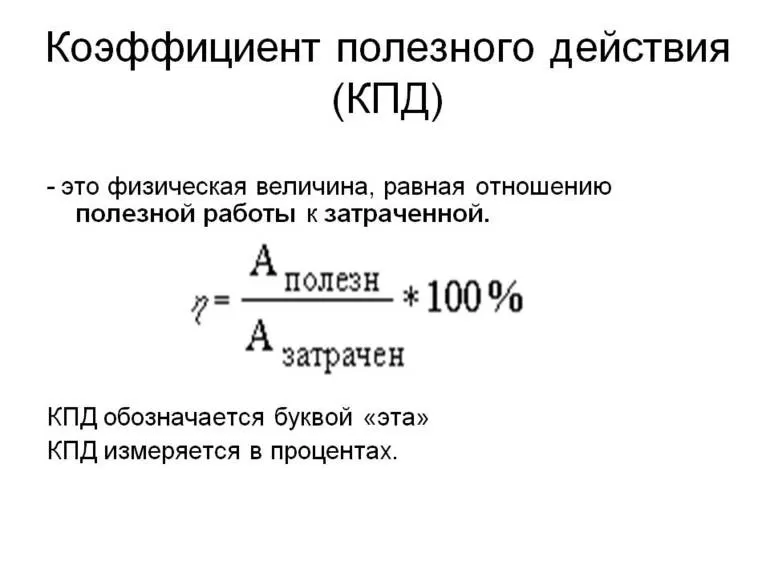
Максимальное значение показателя характерно для циклической машины. Она оперирует при заданных температурах нагревательного элемента (Т1) и холодильника (Т2). Измерение осуществляется по формуле: η= (Т1-Т2)/Т1. Чтобы узнать КПД котла, который функционирует на органическом топливе, используется низшая теплота сгорания.
Плюс теплового насоса как нагревательного прибора заключается в возможности получать больше энергии, чем он может затратить на функционирование. Показатель трансформации вычисляется путём деления тепла конденсации на работу, затрачиваемую на выполнение данного процесса.
Мощность разных устройств
По статистике, во время работы прибора теряется до 25% энергии. При функционировании двигателя внутреннего сгорания топливо сгорает частично. Небольшой процент вылетает в выхлопную трубу. При запуске бензиновый мотор греет себя и составные элементы. На потерю уходит до 35% от общей мощности.
При движении механизмов происходит трение. Для его ослабления используется смазка. Но она неспособна полностью устранить явление, поэтому затрачивается до 20% энергии. Пример на автомобиле: если расход составляет 10 литров топлива на 100 км, на движение потребуется 2 л, а остаток, равный 8 л — потеря.
Если сравнивать КПД бензинового и дизельного моторов, полезная мощность первого механизма равна 25%, а второго — 40%. Агрегаты схожи между собой, но у них разные виды смесеобразования:
- Поршни бензинового мотора функционируют на высоких температурах, поэтому нуждаются в хорошем охлаждении. Тепло, которое могло бы перейти в механическую энергию, тратится впустую, что способствует снижению КПД.
- В цепи дизельного устройства топливо воспламеняется в процессе сжатия. На основе данного фактора можно сделать вывод, что давление в цилиндрах высокое, при этом мотор экологичнее и меньше первого аналога. Если проверить КПД при низком функционировании и большом объёме, результат превысит 50%.
Асинхронные механизмы
Расшифровка термина «асинхронность» — несовпадение по времени. Понятие используется во многих современных машинах, которые являются электрическими и способны преобразовывать соответствующую энергию в механическую. Плюсы устройств:
- простое изготовление;
- низкая цена;
- надёжность;
- незначительные эксплуатационные затраты.
Чтобы рассчитать КПД, используется уравнение η = P2 / P1. Для расчёта Р1 и Р2 применяются общие данные потери энергии в обмотках мотора. У большинства агрегатов показатель находится в пределах 80−90%. Для быстрого расчёта используется онлайн-ресурс либо личный калькулятор. Для проверки возможного КПД у мотора внешнего сгорания, который функционирует от разных источников тепла, используется силовой агрегат Стирлинга. Он представлен в виде тепловой машины с рабочим телом в виде жидкости либо газа. Вещество движется по замкнутому объёму.
Принцип его функционирования основан на постепенном нагреве и охлаждении объекта за счёт извлечения энергии из давления. Подобный механизм применяется на косметическом аппарате и современной подводной лодке. Его работоспособность наблюдается при любой температуре. Он не нуждается в дополнительной системе для запуска. Его КПД возможно расширить до 70%, в отличие от стандартного мотора.
Значения показателя
В 1824 году инженер Карно дал определение КПД идеального двигателя, когда коэффициент равен 100%. Для трактовки понятия была создана специальная машина со следующей формулой: η=(T1 — Т2)/ T1. Для расчёта максимального показателя применяется уравнение КПД макс = (T1-T2)/T1x100%. В двух примерах T1 указывает на температуру нагревателя, а T2 — температуру холодильника.
На практике для достижения 100% коэффициента потребуется приравнять температуру охладителя к нулю. Подобное явление невозможно, так как T1 выше температуры воздуха. Процедура повышения КПД источника тока либо силового агрегата считается важной технической задачей. Теоретически проблема решается путём снижения трения элементов двигателя и уменьшения теплопотери. В дизельном моторе подобное достигается турбонаддувом. В таком случае КПД возрастает до 50%.
Мощность стандартного двигателя увеличивается следующими способами:
- подключение к системе многоцилиндрового агрегата;
- применение специального топлива;
- замена некоторых деталей;
- перенос места сжигания бензина.
КПД зависит от типа и конструкции мотора. Современные учёные утверждают, что будущее за электродвигателями. На практике работа, которую совершает любое устройство, превышает полезную, так как определённая её часть выполняется против трения. Если используется подвижный блок, совершается дополнительная работа: поднимается блок с верёвкой, преодолеваются силы трения в блоке.
Решение примеров
Задача 1. Поезд на скорости 54 км/ч развивает мощность 720 кВт. Нужно вычислить силу тяги силовых агрегатов. Решение: чтобы найти мощность, используется формула N=F x v. Если перевести скорость в единицу СИ, получится 15 м/с. Подставив данные в уравнение, определяется, что F равно 48 kН.
Задача 2. Масса транспортного средства соответствует 2200 кг. Машина, поднимаясь в гору под уклоном в 0,018, проходит расстояние 100 м. Скорость развивается до 32,4 км/ч, а коэффициент трения соответствует 0,04. Нужно определить среднюю мощность авто при движении. Решение: вычисляется средняя скорость — v/2. Чтобы определить силу тяги мотора, выполняется рисунок, на котором отображаются силы, воздействующие на машину:
- тяжесть — mg;
- реакция опоры — N;
- трение — Ftr;
- тяга — F.
Первая величина вычисляется по второму закону Ньютона: mg+N+Ftr+F=ma. Для ускорения используется уравнение a=v2/2S. Если подставить последние значение и воспользоваться cos, получится средняя мощность. Так как ускорение считается постоянной величиной и равно 9,8 м/с2, поэтому v= 9 м/с. Подставив данные в первую формулу, получится: N= 9,5 kBt.
При решении сложных задач по физике рекомендуется проверить соответствие предоставленных в условиях единиц измерения с международными стандартами. Если они отличаются, необходимости перевести данные с учётом СИ.