Как полезная мощность зависит от сопротивления нагрузки
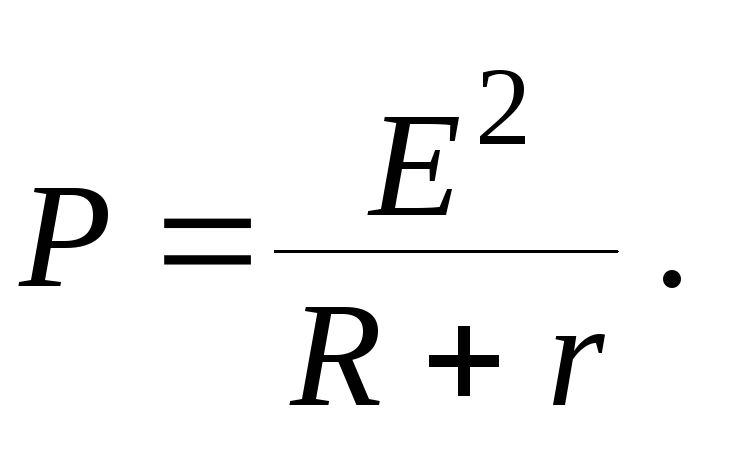
Пишу для школьников (для лучшего понимания ими основ физики). Материал излагаю в соответствии с признанной ныне научной трактовкой физических явлений. Критике существующей теории и глубоким теоретическим рассуждениям здесь не место.
На рисунке изображена замкнутая электрическая цепь, состоящая из источника постоянного тока и переменной нагрузки во внешней части цепи.
Источником постоянного тока может быть электрическая машина, о которой говорится в статье “Искровой разряд”; батарея гальванических элементов, аккумулятор и др.
Роль источника тока заключается в создании (генерировании) электрической энергии: в разделении положительных и отрицательных зарядов; в создании и поддерживании разности потенциалов между конечными точками цепи, в которую включена нагрузка (электрическая лампочка, электроплитка. электродвигатель и т. д.).
При прохождении тока через нагрузку электрическая энергия превращается в другие виды энергии :тепловую (в электроплитке); в тепло и свет (в электрической лампе); в механическую энергию (в электродвигателе).
Превращение энергии из одного вида в другой всегда связано с работой.
При прохождении тока по проводнику совершается работа, её совершают электрические силы (или электрическое поле). Кратко эту работу называют работой тока.
Рассматривая участок цепи, по которому проходит ток, получим следующее выражение для работы тока:
Работа тока равна произведению напряжения между концами участка на протекающий ток и время его протекания.
В случае, если участок цепи однородный (не содержит источника тока), то
тогда получим ещё две формулы для работы тока:
Если ток проходит через неподвижный проводник, то единственным результатом работы тока является его нагревание. Тогда количество выделившейся теплоты
Это запись закона Джоуля – Ленца.
Если кроме нагревания ток совершает ещё механическую работу, например, приводя в действие электродвигатель (мотор), то работа
лишь частично переходит в тепло.
В этом случае работа тока больше количества выделившейся теплоты, но закон Джоуля – Ленца выполняется.
Работа, совершаемая током в единицу времени, называется мощностью тока:
Единицей мощности тока является 1 Вт:
1 Вт – мощность выделяемая током 1 А в проводнике, между концами которого поддерживается напряжение 1 В.
Основная формула мощности для участка цепи:
Мощность постоянного тока на любом участке цепи выражается произведением силы тока на напряжение между концами участка цепи.
Так как для однородного участка цепи
то мощность можно найти ещё по формулам:
Обычно говорят не о работе, а о потребляемой из сети некоторым прибором (электроплитка, лампочки и др.) или двигателем (мотором) мощности электрического тока. Говоря о мощности (например, электродвигателя), отмечают, что работа двигателя совершается за счёт тока.
На приборах часто отмечается потребляемая ими мощность – мощность, необходимая для нормальной работы этого прибора.
Согласно закону сохранения энергии, для замкнутой электрической цепи можно записать:
Здесь
есть полная или затраченная работа, совершаемая сторонними силами, существующими внутри источника, по переносу заряда по цепи.
В гальваническом элементе такими силами являются силы химической реакции.
– это полезная работа, совершаемая электрическим полем при прохождении тока через нагрузку;
это работа, совершаемая внутри источника, по преодолению его внутреннего сопротивления.
Так как работа, совершённая за единицу времени, есть мощность, то из уравнения (1) получим выражение для мощности:
Здесь
есть полная или затраченная мощность, это мощность развиваемая источником тока.
это мощность выделяемая внутри источника тока
это полезная мощность, создаваемая во внешней части цепи (на нагрузке).
Здесь U – напряжение на зажимах источника при замкнутой цепи (при разомкнутой цепи оно равно ЭДС источника).
Так как для однородного участка цепи напряжение равно произведению тока на сопротивление, то полезную мощность можно найти ещё по следующей формуле:
Ток в замкнутой цепи
тогда формулу для полезной мощности можно записать так:
Проанализируем зависимость полезной мощности от сопротивления нагрузки.
При коротком замыкании вся развиваемая источником мощность выделяется на его внутреннем сопротивлении в виде теплоты.
Таким образом, полезная мощность, развиваемая во внешней цепи, достигает максимального значения тогда, когда сопротивление нагрузки равно внутреннему сопротивлению источника.
На следующем рисунке показан график зависимости полезной мощности от сопротивления нагрузки.
Получена формула для нахождения максимальной полезной мощности
При этом ток в цепи в два раза меньше тока короткого замыкания:
Но чему при этом будет равно КПД источника?
Коэффициент полезного действия (КПД) источника показывает, какая часть затраченной (полной) работы источника пошла на пользу или КПД есть отношение полезной работы к затраченной:
Получается, что если добиваться максимальной мощности во внешней цепи, то получим КПД работы всего 50%, то есть половина затраченной мощности источника расходуется бесполезно – переходит в тепло, нагревая источник тока.
Выгоднее брать сопротивление нагрузки больше внутреннего сопротивления источника. Тогда ток в цепи уменьшится, а КПД источника увеличится.
Подумайте над решением следующих задач.
1. ЭДС аккумулятора 2 В, его внутреннее сопротивление 0,4 Ом, сопротивление внешней цепи 1 Ом. Найти разность потенциалов на зажимах аккумулятора и КПД его работы. Ответ: 1,43 В; 71 %.
2. Какую максимальную полезную мощность может выделить аккумулятор с ЭДС 10 В и внутренним сопротивлением 1 Ом? Каково при этом сопротивление внешней цепи? Ответ: 25 Вт; 1 Ом.
3. КПД источника тока, замкнутого на внешнее сопротивление R, равно 60%. Каков будет КПД источника, если внешнее сопротивление увеличить в 6 раз? Ответ: 90%.
Ответ: 7,7 Вт; 12 Вт; 40%; 25%.
Ответ: 2,7 10 4 кг.
К.В. Рулёва
Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Сообщите друзьям о существовании этого канала.
Предыдущая запись: Решение задач на мощность тока.
Следующая запись: Ещё раз о зарядке и разрядке конденсатора.
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Источник
Рассмотрим
зависимость
полной, полезной и внутренней мощности
от внешнего
сопротивления
R
в цепи источника с ЭДС Е
и внутренним сопротивлением r.
Полнаямощность, развиваемая источником, может
быть записана следующим образом, если
в формулу (5) подставить выражение для
тока (1):
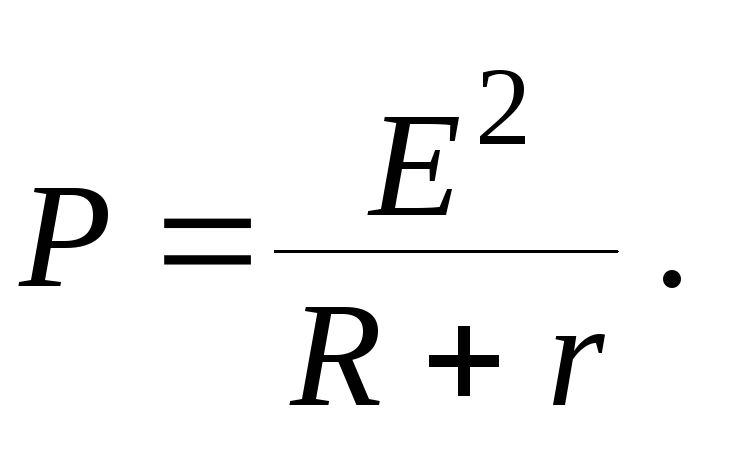 (18)
(18)
Так
полная мощность зависит от сопротивления
нагрузки R.
Она наибольшая при коротком замыкании
цепи, когда сопротивление нагрузки
обращается в нуль (9). С ростом сопротивления
нагрузки R
полная мощность уменьшается, стремясь
к нулю при R
.
На внешнем
сопротивлении выделяется
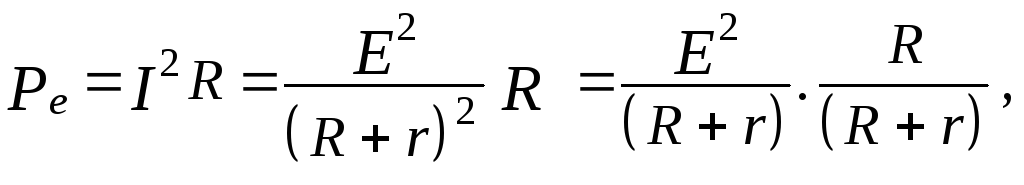 (19)
(19)
![]() (20)
(20)
Внешняя
мощность Ресоставляет
часть полной мощности Р
и ее величина зависит от отношения
сопротивлений R/(R+r).
При коротком замыкании внешняя мощность
равна нулю. При увеличении сопротивления
R
она сначала увеличивается. При Rr
внешняя мощность по величине стремится
к полной. Но сама полезная мощность при
этом становится малой, так как уменьшается
полная мощность (см. формулу 18). При R
внешняя мощность стремятся к нулю как
и полная.
Каково
должно быть сопротивление нагрузки,
чтобы получить от данного источника
максимальную
внешнюю (полезную) мощность (19)?
![]()
Найдем
максимум этой функции из условия:

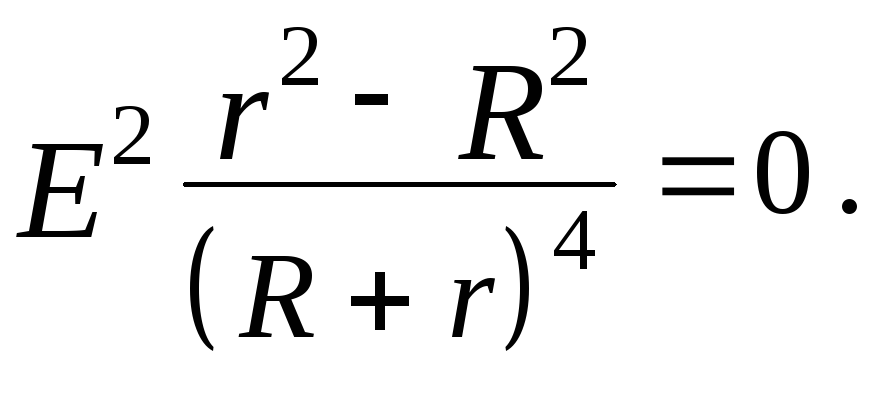
Решая
это уравнение, получаем Rmax=
r.
Таким
образом, во
внешней цепи выделяется максимальная
мощность, если ее сопротивление равно
внутреннему сопротивлению источника
тока. При
этом условии ток в цепи равен E/2r,
т.е. половине
тока короткого замыкания (8). Максимальная
полезная мощность при таком сопротивлении
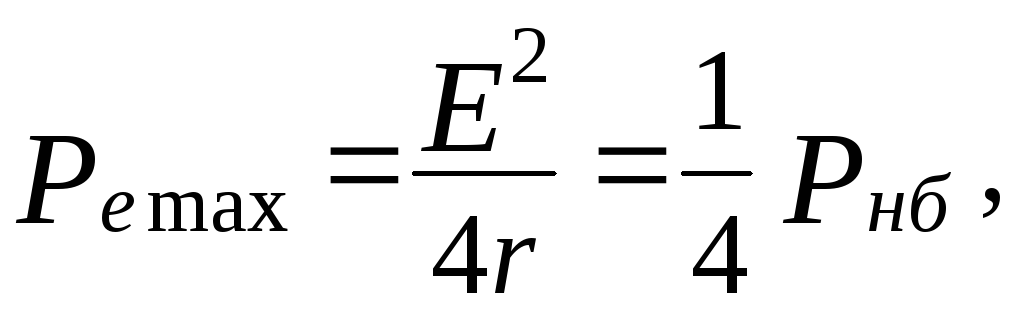 (21)
(21)
что
совпадает с тем, что было получено выше
(12).
Мощность, выделяющаяся
на внутреннем сопротивлении источника
![]() (22)
(22)
При
RPiP,
а при R=0
достигает наибольшей величины Pi
нб=Pнб=E2/r.
При R=r
внутренняя мощность составляет половину
полной, Pi=P/2.
При Rr
она уменьшается почти так же, как и
полная (18).
Зависимость
КПД от сопротивления внешней части цепи
выражается следующим образом:
=
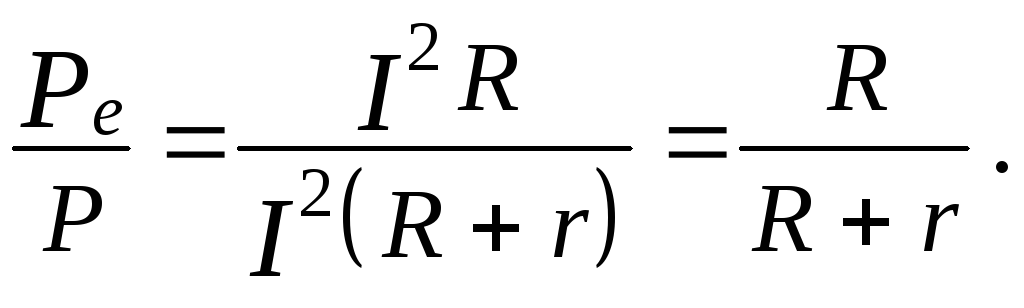 (23)
(23)
Из
полученной формулы вытекает, что КПД
стремится к нулю при приближении
сопротивления нагрузки к нулю, и КПД
стремится к наибольшему значению,
равному единице, при возрастании
сопротивления нагрузки до Rr
. Но полезная мощность при этом уменьшается
почти как 1/R(см. формулу
19).
Мощность
Ре
достигает максимального значения при
Rmax=
r,
КПД при этом равен, согласно формуле
(23),
= r/(r+r)
= 1/2. Таким
образом, условие
получения максимальной полезной мощности
не совпадает с условием получения
наибольшего КПД.
Наиболее
важным результатом проведенного
рассмотрения является оптимальное
согласование параметров источника с
характером нагрузки. Здесь можно выделить
три области: 1)Rr,
2)Rr,
3) Rr.
Первый
случай имеет место там, где от источника
требуется малая мощность в течение
длительного времени, например, в
электронных часах, микрокалькуляторах.
Размеры таких источников малы, запас
электрической энергии в них небольшой,
она должна расходоваться экономно,
поэтому они должны работать с высоким
КПД.
Второй
случай – короткое замыкание в нагрузке,
при котором вся мощность источника
выделяется в нем и проводах, соединяющих
источник с нагрузкой. Это приводит к их
чрезмерному нагреванию и является
довольно распространенной причиной
возгораний и пожаров. Поэтому короткое
замыкание источников тока большой
мощности (динамо-машины, аккумуляторные
батареи, выпрямители) крайне опасно.
В третьемслучае от источника хотят получить
максимальную мощность хотя бы накороткоевремя, например, при запуске двигателя
автомобиля с помощью электростартера,
величина КПД при этом не так уж важна.
Стартер включается на короткое время.
Длительная эксплуатация источника в
таком режиме практически недопустима,
так как она приводит к быстрому разряду
автомобильного аккумулятора, его
перегреву и прочим неприятностям.
Для обеспечения
работы химических источников тока в
нужном режиме их соединяют между собой
определенным образом в так называемые
батареи. Элементы в батарее могут
соединяться последовательно, параллельно
и по смешанной схеме. Та или иная схема
соединения определяется сопротивлением
нагрузки и величиной потребляемого
тока.
Важнейшим
эксплуатационным требованием к
энергетическим установкам является
высокий КПД их работы. Из формулы (23 )
видно, что КПД стремится к единице, если
внутреннее сопротивление источника
тока мало по сравнению с сопротивлением
нагрузки
Параллельно
можно соединять элементы, имеющие
одинаковые
ЭДС. Если соединено nодинаковых
элементов, то от такой батареи можно
получить ток
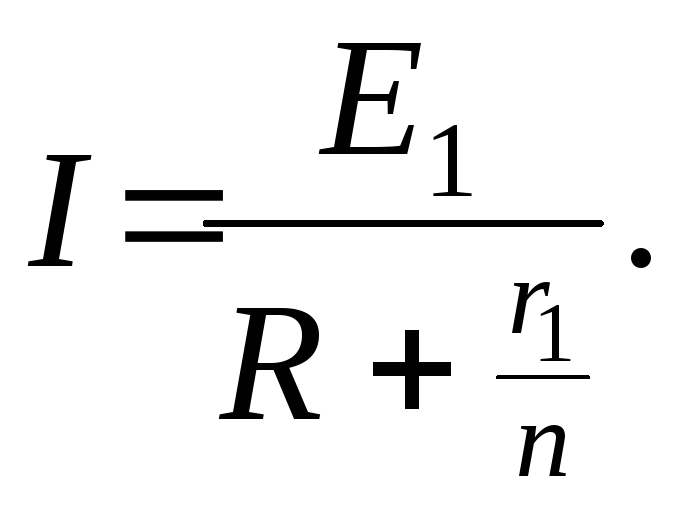 (24)
(24)
Здесь
r1
– сопротивление
одного элемента, Е1
– ЭДС одного
элемента.
Такое
соединение выгодно применять при
низкоомной нагрузке, т.е. при Rr.
Так как общее внутреннее сопротивление
батареи при параллельном соединении
уменьшается в nраз по
сравнению с сопротивлением одного
элемента, то его можно сделать близким
сопротивлению нагрузки. Благодаря
этому увеличивается КПД источника.
Возрастает в nраз и
энергетическая емкость батареи элементов.
Если
нагрузка высокоомная, т.е. Rr,
то выгоднее соединять элементы в батарею
последовательно. При этом ЭДС батареи
будет в nраз больше
ЭДС одного элемента и от источника можно
получить необходимый ток
![]() .
.
(25)
Целью
данной
лабораторной работы является
экспериментальная
проверка
полученных выше теоретических результатов
о зависимости полной, внутренней и
внешней (полезной) мощности и КПД
источника как от силы потребляемого
тока, так и от сопротивления нагрузки.
Описание
установки.
Для исследования рабочих характеристик
источника тока применяется электрическая
цепь, схема которой показана на рис. 4.
В качестве источника тока используются
два щелочных аккумулятора НКН-45, которые
соединяютсяпоследователь-но
в одну батарею
через резистор r, моделирующий
внутреннее сопро-тивление источника.
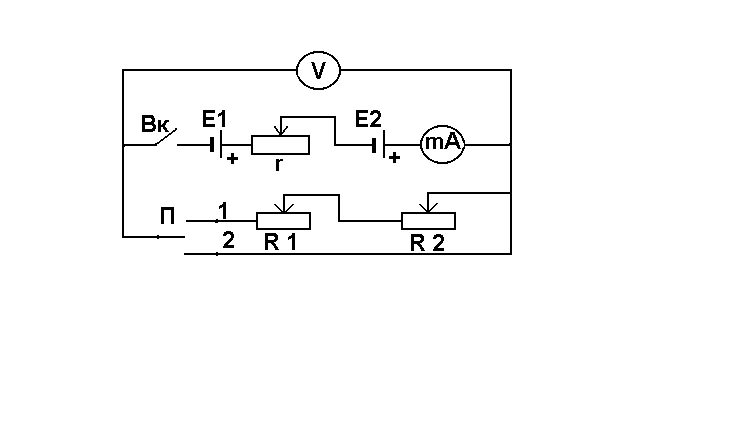
Его включение искусственно
увеличивает внутреннее сопротивление
аккуму-ляторов, что 1)защищает их от
перегрузки при переходе в режим короткого
замыкания и 2)дает возможность изменять
внутреннее сопротивление источника по
желанию экспериментатора. В качестве
нагрузки (внешнего сопротивления цепи)
п
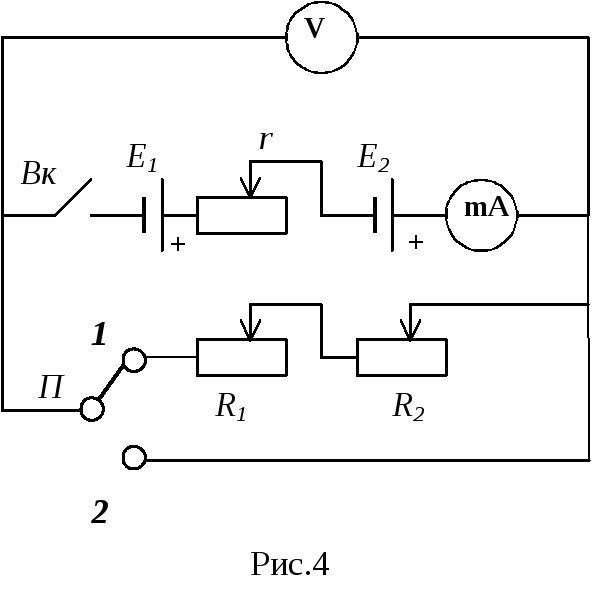 рименяются
рименяются
два переменных резистораR1иR2.
(один грубой регулировки, другой –
тонкой), что обеспечивает плавное
регулирование тока в широком диапазоне.
Все приборы
смонтированы на лабораторной панели.
Резисторы закреплены под панелью, наверх
выведены их ручки управления и клеммы,
около которых имеются соответствующие
надписи.
Измерения.
1.Установите переключатель П
в нейтральное
положение, выключатель Вк
разомкните.
Ручки резисторов поверните против
часовой стрелки до упора ( это соответствует
наибольшему сопротивлению нагрузки).
Соберите
электрическую цепь по схеме (рис. 4), не
присоединяя
пока источники
тока.После
проверки собранной цепи преподавателем
или лаборантом присоедините аккумуляторы
Е1и Е2
, соблюдая
полярность.Установите
ток короткого замыкания. Для этого
поставьте переключатель П
в положение 2 (внешнее сопротивление
равно нулю) и с помощью резистора r установите
стрелку миллиамперметра на предельное
(правое крайнее) деление шкалы прибора
– 75 или 150 мА. Благодаря резистору r
в лабораторной установке есть возможность
регулировать
внутреннее сопротивление источника
тока. На самом деле внутреннее
сопротивление – величина постоянная
для данного типа источников и изменить
его невозможно.Поставьте
переключатель П
в положение 1,
включив тем самым внешнее сопротивление
(нагрузку) R=R1+R2
в цепь источника.Изменяя
ток в цепи через 5…10 мА от наибольшего
до наименьшего значения с помощью
резисторов R1
иR2,
запишите показания миллиамперметра и
вольтметра (напряжение на нагрузке U)
в таблицу.Поставьте
переключатель П
в нейтральное положение. В этом случае
к источнику тока присоединен только
вольтметр, который обладает довольно
большим сопротивлением по сравнению
с внутренним сопротивлением источника,
поэтому показание вольтметра будет
чуть-чуть меньше ЭДС источник. Поскольку
у вас нет другой возможности определить
ее точное значение, остается принять
показание вольтметра за Е.
(Подробнее об этом см. в лабораторной
работе № 311).
№ пп | I, мА | U, B | E, B | P, Вт | Pe, Вт | Pi, Вт | R, Ом | |
Обработка
результатов.
1. Для каждого значения тока вычислите:
полную мощность
по формуле (5),внешнюю
(полезную) мощность по формуле
,внутреннюю
мощность из соотношениясопротивление
внешнего участка цепи из закона Ома
R=U/I,КПД источника
тока по формуле (16).
Постройте графики
зависимостей:
полной,
полезной и внутренней мощности от тока
I(на одном
планшете),полной,
полезной и внутренней мощности от
сопротивления R
(также на одном планшете); разумней
построить только часть графика,
соответствующего его низкоомной части,
и отбросить 4-5 экспериментальных точек
из 15 в высокоомной области,КПД
источника от величины потребляемого
тока I,КПД
от сопротивления нагрузки R.
Из
графиков Pe отI иPeотRопределите
максимальную полезную мощность во
внешней цепи Pemax.Из
графика Pe отR определите
внутреннее сопротивление источника
тока r.Из
графиков Pe отIиPe отR найдите
КПД источника тока при Imaxи при Rmax.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник

Давайте вместе разберемся в зависимости сопротивления, напряжения, силы тока и мощности на примере движения воды. В реальном времени на наших интерактивных примерах вы сможете увидеть как изменяется один из искомых параметров, если вы знаете величины двух других.
Существует всего 2 базовых формулы которые помогут вам понять взаимосвязь между силой тока(Амер), напряжением(Вольт), сопротивлением (Ом) и мощностью (Ватт).
Зная хотя бы два из перечисленных параметра вы всегда можете рассчитать два других.
ЗАКОН ОМА
| Базовая формула | P=I*E | E=I*R | |
| Расчет напряжения | E=P/I | E=I*R | E=SQR(P*R) |
| Расчет силы тока | I=P/E | I=E/R | I=SQR(P/R) |
| Расчет мощности | P=I*E | P=E 2 /R | P=I 2 *R |
| Расчет сопротивления | R=E 2 /P | R=E/I | R=P/I 2 |
P — Мощность (Ватт)
E — Напряжение (Вольт)
I — Сила тока (Ампер)
R — Электрическое сопротивление (Ом)
SQR — квадратный корень
Мы используем переменную E для обозначения напряжения, иногда вы можете встретить обозначение V для напряжения. Не дайте себя запутать названиям переменных.
Изменение сопротивления:
На следующей схеме вы видите разность сопротивлений между системами изображенными на правой и левой стороне рисунка. Сопротивление давлению воды в кране противодействует задвижка, в зависимости от степени открытия задвижки изменяется сопротивление.
Сопротивление в проводнике изображено в виде сужения проводника, чем более узкий проводник тем больше он противодействует прохождению тока.
Вы можете заметить что на правой и на левой стороне схемы напряжение и давление воды одинаково.
Вам необходимо обратить внимание на самый важный факт.
В зависимости от сопротивления увеличивается и уменьшается сила тока.
Слева при полностью открытой задвижке мы видим самый большой поток воды. И при самом низком сопротивлении, видим самый большой поток электронов (Ампераж) в проводнике.
Справа задвижка закрыта намного больше и поток воды тоже стал намного больше.
ужение проводника тоже уменьшилось вдвое, я значит вдвое увеличилось сопротивление протеканию тока. Как мы видим через проводник из за выского сопротивления протекает в два раза меньше электронов.
Обратите внимание что сужение проводника изображенное на схеме используется только для примера сопротивления протеканию тока. В реальных условиях сужения проводника не сильно влияет на протекающий ток. Значительно большее сопротивление могут оказывать полупроводники и диэлектрики.
Сужающийся проводник на схеме изображен лишь для примера, для понимания сути происходящего процесса.
Формула закона Ома — зависимость сопротивления и силы тока
Как вы видите из формулы, сила тока обратнапропорциональна сопротивлению цепи.
Больше сопротивление = Меньше ток
* при условии что напряжение постоянно.
Изменение напряжения.
На изображенной схеме во всех системах сопротивление имеет одинаковую величину.
В этот раз на картинке изменяется сопротивление/давление.
Вы можете увидеть что при увеличении напряжения приводит к увеличению протекающего тока даже при постоянном сопротивлении.
Формула закона Ома — зависимость напряжения и силы тока
Обратите внимание что сила тока протекающего в проводнике прямопропорциональна напряжению.
Больше напряжение = Больше сила тока
* при условии что сопротивление постоянно.
Математический рассчет
Рассмотрим пример.
У нас есть аккумуляторная батарея с напряжением питания 12 Вольт. К ней напрямую подключен резистор (сопротивление) 10 Ом. Для того что бы рассчитать какая мощность приложена к нашему резистору, можно воспользоваться формулой.
P = E2/R
P = 122/10
P = 144/10.
P = 14.4 watts
Мощность рассеиваемая на резисторе состовляет 14,4 Ватта.
Если вы хотите определить величину тока протекающего через проводник, мы используем другую формулу
I = E/R
I = 12/10
I = 1.2 amps
Сила тока протекающего через цепь составляет 1,2 Ампера
—————-
Калькуляторы зависимости напряжения, силы тока и сопротивления.
1. Калькулятор рассеиваемой мощности и протекающей силы тока в зависимости от сопротивления и приложенного напряжения.
Демо закона Ома в реальном времени.
Для справки
В данном примере вы можете увеличивать напряжение и сопротивление цепи. Данные изменения в реальном времени будут изменять силу тока протекающего в цепи и мощность рассеиваемую на сопротивлении.
Если рассматривать аудио системы — вы должны помнить что усилитель выдает определенное напряжение на определенную нагрузку (сопротивление). Соотношение двух этих величин определяет мощность.
Усилитель может выдать ограниченную величину напряжения в зависимости от внутреннего блока питания и источника тока. Так же точно ограничена и мощность которую может подать усилитель на определенную нагрузку (к примеру 4 Ома).
Для того что бы получить больше мощности, вы можете подключить к усилителю нагрузку с меньшим сопротивлением (к примеру 2 Ома). Учтите что при использовании нагрузки с меньшим сопротивлением — скажем в два раза (было 4 Ома, стало 2 Ома) — мощность тоже возрастет в два раза.(при условии что данную мощность может обеспечить внутренний блок питания и источник тока).
Если мы возьмем для примера моно усилитель мощностью 100 Ватт на нагрузку 4 Ома, зная что он может выдать напряжение не более 20 Вольт на нагрузку.
Если вы поставите на нашем калькуляторе бегунки
Напряжение 20 Вольт
Сопротивление 4 Ома
Вы получите
Мощность 100 Ватт
Если вы сдвинете бегунок сопротивления на величину 2 Ома, вы увидите как мощность удвоится и составит 200 Ватт.
В общем примере источником тока является аккумуляторная батарея (а не усилитель звука) но зависимости силы тока, напряжения, сопротивления и сопротивления одинаковы во всех цепях.
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На уроке речь пойдет об одном из центральных законов электродинамики – законе Ома для участка цепи. Будет изложена история его получения и указана формула с графической зависимостью.
История открытия закона Ома для участка цепи
Вспомним, что несколько предыдущих уроков были посвящены изучению таких физических величин, как сила тока, напряжение и сопротивление. Мы рассмотрели природу возникновения электрического сопротивления, единицу его измерения и вкратце указали, от каких общих факторов оно зависит. Также мы знаем, что сила тока зависит от электрического поля, которое возникает в проводнике, а напряжение зависит от работы этого поля. Но электрический ток – это упорядоченное движение заряженных частиц, которое также характеризуется работой электрического тока. Следовательно, должна быть какая-нибудь связь между всеми этими понятиями: сила тока, напряжение, сопротивление.
Впервые определил эту зависимость в 1826 году немецкий физик Георг Ом (1789–1854) (рис. 1). Он провел очень большое количество экспериментов, в которых, прежде всего, исследовал зависимость силы тока в цепи от напряжения. Проводились его эксперименты следующим образом: ничего не меняя в электрической цепи, он подключал к ней различное большее число источников тока, в результате чего увеличивалось напряжение, подаваемое в цепь, что приводило к увеличению силы тока. Такие многочисленные эксперименты привели к получению закона силы тока от электрического сопротивления.
Опишем схему проведения экспериментов Георга Ома. В электрическую цепь он подключал проводник, на котором с помощью вольтметра и амперметра измерялись напряжение и сила тока соответственно, ключ и источник тока (рис. 2). Обратим внимание на то, что в цепи подключено несколько источников тока, и изменение их количества позволяет пронаблюдать за изменением силы тока в цепи в зависимости от напряжения.
Рис. 2. Схема экспериментов Г. Ома
В результате измерений прослеживается зависимость , где напряжение измеряется на зажимах AB, т. е. на проводнике.
Для того чтобы пронаблюдать зависимость силы тока от сопротивления, в той же цепи теперь следует не менять количество источников тока, а менять проводники, т. е. сопротивление цепи. Георг Ом поступил следующим образом: вместо одного проводника он подключил другой с вдвое большей длиной, т. е. с вдвое большим сопротивлением (почему это так, вы узнаете на следующем уроке). Аналогично он подключал и проводники с другими длинами и получил зависимость такого вида: . Т. е. при увеличении сопротивления проводника сила тока в нем уменьшается.
На графике зависимость силы тока в проводнике от сопротивления выглядит следующим образом (рис. 3).
Рис. 3. Зависимость силы тока в проводнике от сопротивления
Такая зависимость называется обратно пропорциональной. Эту зависимость Ому пришлось достаточно долго получать, но именно это и привело его к выводу важнейшего закона электродинамики – закону Ома для участка цепи. Собрав вместе те две зависимости, которые мы показали выше, Ом и пришел к своему закону.
Закон Ома для участка цепи
Закон Ома для участка цепи: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению:
Замечание. Этот закон лежит в основе науки под названием электротехника.
Т. к. напряжение в законе рассматривается на концах проводника и учитывается сопротивление самого проводника, то закон применим именно к участку цепи, т. е. к какой-либо его части.
напряжение, В;
сила тока, А;
сопротивление, Ом.
При работе с законом Ома следует понимать, что он выполним отдельно для каждого рассматриваемого участка цепи с различными значениями входящих в него параметров.
На следующем уроке речь пойдет о том, от каких параметров зависит сопротивление проводника.
Список литературы
- Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
- Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
- Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
1. Стр. 102: вопросы № 1–7, упражнение № 19. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
2. Вычислите силу тока в резисторе, сопротивление которого – 1200 Ом, а напряжение – 36 В.
3. Каким образом изменится сила тока в цепи, если количество последовательно соединенных источников тока в ней увеличить втрое, а подключенный к ней проводник укоротить вдвое? Кроме проводника и источников тока в цепи элементов нет.
4. * Соберите с помощью родителей или учителя схему, аналогичную той, с помощью которой Георг Ом получил свой известный закон. Проведите серию экспериментов, доказывающую справедливость закона Ома для участка цепи. Оцените погрешности измерений и результаты обсудите с учителем.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Как рассчитать мощность резистора?
У резистора есть довольно важный параметр, который целиком и полностью влияет на надёжность его работы. Этот параметр называется мощностью рассеивания. Он уже упоминался в статье о параметрах резистора.
Сама по себе мощность постоянного тока рассчитывается по простой формуле:
Как видим, мощность зависит от напряжения и тока. В реальной цепи через резистор протекает определённый ток. Поскольку резистор обладает сопротивлением, то под действием протекающего тока резистор нагревается. На нём выделяется какое-то количество тепла. Это и есть та мощность, которая рассеивается на резисторе.
Если в схему установить резистор меньшей мощности рассеивания, чем требуется, то резистор будет нагреваться и в результате сгорит. Поэтому, если в схеме нужно заменить резистор мощностью 0,5 Ватт, то ставим на 0,5 Ватт и более. Но никак не меньше !
Каждый резистор рассчитан на свою мощность. Стандартный ряд мощностей рассеивания резисторов состоит из значений:
Чем больше резистор по размерам, тем, как правило, на большую мощность рассеивания он рассчитан.
Допустим, у нас есть резистор с номинальным сопротивлением 100 Ом. Через него течёт ток 0,1 Ампер. На какую мощность должен быть рассчитан этот резистор?
Тут нам потребуется формула. Выглядит она так:
R(Ом) – сопротивление цепи (в данном случае резистора);
I(А) – ток, протекающий через резистор.
Все расчёты следует производить, строго соблюдая размерность. Так, если сопротивление резистора не 100 Ом, а 1 кОм, то в формулу нужно подставить значение в Омах, т.е. 1000 Ом (1 кОм = 1000 Ом). Тоже правило касается и других величин (тока, напряжения).
Рассчитаем мощность для нашего резистора:
Мы получили мощность 1 Ватт. Теперь небольшое отступление.
В реальную схему необходимо устанавливать резистор с мощностью в полтора – два раза выше рассчитанной.
Поэтому нам подойдёт резистор мощностью 2 Вт (см. стандартный ряд мощностей резисторов).
Также есть и другая формула для расчёта мощности. Она применяется в том случае, если неизвестен ток, который протекает через резистор.
Всё бы хорошо, но в жизни бывают случаи, когда применяется последовательное или параллельное соединение резисторов. Как рассчитать мощность рассеивания для каждого из резисторов в последовательной или параллельной цепи?
Допустим, нам требуется заменить резистор сопротивлением 100 Ом. Протекающий через него ток равен 0,1 Ампер. Следовательно, мощность этого резистора 1 Ватт.
Для его замены можно применить два соединённых последовательно резистора сопротивлением 20 Ом и 80 Ом. На какую мощность должны быть рассчитаны эти резисторы?
Для последовательной цепи действует одно правило. Через последовательно соединённые резисторы течёт один и тот же ток. Теперь применим формулу для расчёта мощности и получим, что мощность рассеивания резистора на 20 Ом должна быть равна 0,2 Вт, а резистора на 80 Ом — 0,8 Вт. Выбираем резисторы согласно стандартному ряду мощностей:
Как видим, если сопротивления резисторов будут разные, то и мощность на них будет выделяться разная.
Мощность, рассеивающаяся на резисторе, зависит в первую очередь от тока, который течёт через данный резистор. А ток зависит от сопротивления резистора. Поэтому, если вы соединяете последовательно резисторы разных номиналов, то и рассеивающаяся мощность распределиться между ними.
Это обстоятельство необходимо учитывать при самостоятельном конструировании электронных самоделок иначе при неправильном подборе резисторов может получиться так, что на одном резисторе выделиться больше мощности, чем на другом, и он будет работать в тяжёлом температурном режиме.
Чтобы не ломать голову и не рассчитывать мощность каждого в отдельности резистора, можно поступать так:
Мощность каждого резистора, входящего в составляемую нами цепь (параллельную или последовательную) должна быть равна мощности заменяемого резистора. Иными словами, если нам надо заменить резистор, мощностью 1 Вт, то каждый из резисторов для его замены должен иметь мощность не менее 1 Ватта. На практике это самое быстрое и эффективное решение.
Для параллельного соединения резисторов нужно учитывать, что через резистор с меньшим сопротивлением протекает больший ток. Следовательно, и мощности на нём будет рассеиваться больше.
«>
No related posts.
Оля
Вкусно жить -целая наука!
Источник
