Как найти высоту при массе и полезной энергии
Êëèêíèòå, ÷òîáû äîáàâèòü â èçáðàííûå ñåðâèñû.
Êëèêíèòå, ÷òîáû óäàëèòü èç èçáðàííûõ ñåðâèñîâ.
Êàëüêóëÿòîð Ïîòåíöèàëüíàÿ ýíåðãèÿ òåëà, îíëàéí ðàñ÷åò ïîçâîëÿåò ðàññ÷èòàòü ïîòåíöèàëüíóþ ýíåðãèþ òåëà, îïðåäåëåííîé ìàññû, ïàäàþùåãî ñ îïðåäåëåííîé âûñîòû. À òàêæå îïðåäåëèòü çàâèñèìîñòü ìàññû, âûñîòû è ïîòåíöèàëüíîé ýíåðãèè òåëà äðóã îò äðóãà.
Ðàññ÷èòàòü ïîòåíöèàëüíóþ ýíåðãèþ, ìàññó èëè âûñîòó | |
| Ïîòåíöèàëüíàÿ ýíåðãèÿ Ìàññà Âûñîòà | |
| Ìàññà: | |
| Âûñîòà: | |
| Ðåçóëüòàò â: | |
| Ïîòåíöèàëüíàÿ ýíåðãèÿ òåëà – ýòî ñêàëÿðíàÿ ôèçè÷åñêàÿ âåëè÷èíà, ðàâíàÿ ðàáîòå, ñîâåðøàåìîé ïîòåíöèàëüíîé ñèëîé ïðè ïåðåìåùåíèè òåëà èç îäíîé òî÷êè â äðóãóþ, ïîòåíöèàëüíàÿ ýíåðãèÿ êîòîðîé ïðèíÿòà çà íîëü. ãäå m – ìàññà òåëà, g – óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ, ðàâíîå 9.8 ì/ñ2, h – âûñîòà òåëà íàä ïðîèçâîëüíî âûáðàííûì íóëåâûì óðîâíåì. | |
|
| ||||||||||||
|
| ||||||||||||
Ìû â ñîöñåòÿõ Ïðèñîåäèíÿéòåñü! Íàøëè îøèáêó? Åñòü ïðåäëîæåíèÿ? Ñîîáùèòå íàì |
Ýòîò êàëüêóëÿòîð ìîæíî âñòàâèòü íà ñàéò, â áëîã Ñîçäàäèì êàëüêóëÿòîð äëÿ âàñ |
Источник
А почему-бы и нет? У нас уже были задачи на свободное падение, законы Ньютона, силу трения и проч. и проч. Сегодня решаем задачи на кинетическую и потенциальную энергию.
А вообще, помните, что мы занимаемся далеко не только решением задач. Наш телеграм – это полезная информация для студентов всех специальностей, новости, лайфхаки, акции и скидки.
Задачи на кинетическую и потенциальную энергию
Приведем примеры задач на нахождение кинетической и потенциальной энергии с решением. Прежде чем приступать к практике, почитайте теорию по теме, повторите общую памятку по решению задач по физике и на всякий случай держите под рукой полезные формулы.
Задача №1 на кинетическую энергию
Условие
Максимальная высота, на которую поднимается тело массой 1 кг, подброшенное вертикально вверх, составляет 20 м. Найдите, чему была равна кинетическая энергия сразу же после броска.
Решение
Потенциальная энергия тела над поверхностью Земли составляет:
Здесь m – масса тела, g – ускорение свободного падения, h – высота. Согласно закону сохранения энергии, потенциальная энергия тела в наивысшей точке должна равняться кинетической энергии тела в начальный момент, то есть:
Принимая ускорение свободного падения равным 10 м/с2, находим кинетическую энергию тела сразу же после броска:
Ответ: 200 Дж.
Задача №2 на потенциальную энергию
Условие
Чему равна потенциальная энергия трех кубических дециметров воды на высоте 10 м?
Решение
По определению, потенциальная энергия равна в поле силы тяжести равна:
Масса трех кубических дециметров воды (трех литров) легко находится из формулы для плотности воды:
Осталось вычислить потенциальную энергию:
Ответ: 300 Дж.
При решении задач не забывайте переводить все размерности величин в систему СИ.
Задача №3 на полную механическую энергию
Условие
Какова полная механическая энергия дирижабля массой 5 тонн, если он летит на высоте 2 км со скоростью 60 км/ч?
Решение
Полная механическая энергия состоит из кинетической и потенциальной энергий:
Вычислим:
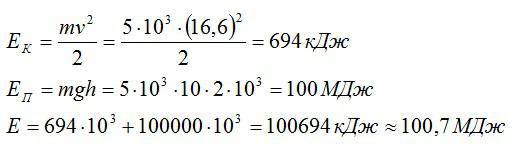
Ответ: 100,7 МДж.
Задача №4 на кинетическую и потенциальную энергию
Условие
Шарик массой 200 г падает с высоты 20 м с начальной скоростью, равной нулю. Какова его кинетическая энергия в момент перед ударом о землю, если потеря энергии за счет сопротивления воздуха составила 4 Дж? (Ответ дайте в джоулях.) Ускорение свободного падения принять равным 10 м/с2.
Решение
Перед началом падения потенциальная энергия шарика составляет:
По закону сохранения энергии, эта энергия должна перейти в кинетическую энергию Ек за вычетом потери за счет сопротивления воздуха дельта Е. Таким образом, можем найти кинетическую энергию:
Ответ: 36 Дж.
Задача №5 кинетическую и потенциальную энергию
Условие
Шарик висит на нити. В нем застревает пуля, летящая горизонтально, в результате чего нить отклоняется на некоторый угол. Как изменятся при увеличении массы шарика следующие величины: импульс, полученный шариком в результате попадания в него пули; скорость, которая будет у шарика тотчас после удара; угол отклонения нити?
Решение
Согласно закону сохранения импульса, скорость шарика с застрявшей в нем пулей равна
Здесь M и m – массы шарика и пули соответственно, v – скорость пули перед ударом. Таким образом, при увеличении массы шарика его скорость после удара уменьшится.
Найдем импульс, переданный шарику при попадании пули:
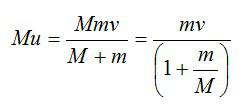
Следовательно, с увеличением массы шарика переданный ему импульс увеличивается.
Согласно закону сохранения энергии, кинетическая энергия пули перейдет в потенциальную энергию шарика с пулей:
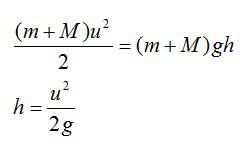
Таким образом, при увеличении массы шарика угол отклонения нити уменьшится, поскольку уменьшится скорость u.
Ответ: см решение выше.
Вопросы на потенциальную и кинетическую энергию
Вопрос 1. Что такое энергия? Что такое механическая энергия?
Ответ. Для энергии существует множество определений. В наиболее общем смысле:
Энергия – мера способности тела совершать работу.
Механическая энергия – это энергия, связанная с движением тела или его положением в пространстве. Механическая энергия в механике описывается суммой кинетической и потенциальной энергии.
Вопрос 2. Сформулируйте закон сохранения энергии
Ответ. Закон сохранения энергии является фундаментальным физическим принципом. Для каждого вида энергии он имеет свою формулировку. Для механической энергии:
Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается неизменной.
Вопрос 3. Какие силы называются консервативными?
Ответ. Консервативные, или потенциальные силы – это силы, работа которых не зависит от формы траектории. В качестве примера такой силы можно привести силу тяжести.
Вопрос 4. Какую энергию называют кинетической?
Ответ. Кинетическая энергия является энергией движения. Ею обладают только движущиеся тела, она зависит от массы тела и его скорости.
Вопрос 5. Какую энергию называют потенциальной?
Ответ. Потенциальная энергия является энергией взаимодействия в поле консервативных сил. Она зависит от положения тела и выбора системы отсчета. Например, потенциальная энергия тела в поле силы тяжести зависит от массы тела, ускорения свободного падения и высоты над нулевым уровнем.
Не знаете, как решать задачи на кинетическую или потенциальную энергию? Проблемы с выполнением любых других студенческих работ? Обращайтесь в профессиональный сервис для учащихся за помощью и консультациями.
Источник
Энергия характеризует способность тела совершать работу. Натянутая тетива лука, сжатая пружина, поднятый с земли камень, сжатый газ при определённых условиях могут совершать работу.
Потенциальной энергией обладают:
1. Тела, поднятые над поверхностью земли (например, камень при падении с высоты образует на земле воронку).
2. Упруго деформированные тела (например, человек натягивает тетиву лука и выпускает стрелу).
3. Сжатые газы (расстояние между молекулами газа уменьшается, и увеличивается сила отталкивания между ними).
Слово «потенциальный» (potentia) на греческом языке означает «возможность».
Огромной потенциальной энергией обладают воды водопада. Потенциальная энергия воды совпадает с работой силы притяжения Земли.
Потенциальная энергия накапливается в водах рек. Сила притяжения Земли производит работу, заставляя реки течь в более низко расположенное место — в море. Человек научился полезно использовать потенциальную энергию рек. В древние времена строили водяные мельницы, а с (20) века — гидроэлектростанции (ГЭС).
Гидроэлектростанция в Итайпу, находящаяся на границе между Бразилией и Парагваем на реке Парана, на сегодня является крупнейшим действующим сооружением такого рода в мире. У её плотины (через которую протекает вода) имеются шлюзы, состоящие из (14) ворот, через которые за секунду проходит (62200) кубометров воды.
Потенциальную энергию тела, поднятого над опорой на высоту (h), рассчитывают по формуле:
Epot=mgh , где m — масса тела, а g — ускорение свободного падения у поверхности Земли.
Потенциальную энергию тела измеряют относительно некоторого условного уровня отсчёта, чаще всего относительно поверхности Земли. В таком случае принимают, что потенциальная энергия тела на поверхности Земли равна нулю.
Обрати внимание!
Тело одновременно может обладать и потенциальной, и кинетической энергией, и они могут переходить одна в другую.
Человек, качающийся на качелях, обладает максимальной потенциальной энергией в наивысшей точке подъёма, в этой точке качели на мгновение замирают и, значит, в этот момент кинетическая энергия человека равна нулю.
При движении из состояния (1) в состояние (2), потенциальная энергия уменьшается, а кинетическая растёт (так как высота тела над уровнем земли уменьшается, а скорость движения тела возрастает).
Когда человек находится в самой нижней точке траектории движения (2), кинетическая энергия является наибольшей, так как в этот его момент скорость самая высокая. При движении из состояния (2) в состояние (3), увеличивается потенциальная энергия (так как увеличивается высота подъёма тела), а кинетическая энергия уменьшается (так как скорость движения тела уменьшается).
В замкнутой системе сумма кинетической и потенциальной энергии в любой момент времени остаётся неизменной.
Сумма потенциальной и кинетической энергии тела называется полной механической энергией тела.
Привязанный отвес на высоте (h) обладает максимальной потенциальной энергией, а кинетическая энергия (энергия движения) в это время равна (0).
Когда верёвку перерезают, отвес начинает свободно падать, высота уменьшается, а скорость увеличивается (с ускорением (g)), соответственно, потенциальная энергия уменьшается, а кинетическая энергия возрастает.
В каждый момент времени, до момента соударения, сумма потенциальной и кинетической энергии отвеса одинакова.
В момент соударения энергия отвеса не исчезает, она передаётся другому телу — гвоздю, который под воздействием этой энергии начинает движение, уходя глубже в брус. Некоторая часть энергии преобразуется во внутреннюю — тепловую энергию (так как отвес при соударении нагревается).
Любое тело обладает внутренней энергией, которая не связана с движением тела.
Внутреннюю энергию образует движение атомов и молекул тела.
Например, в результате удара частички начинают двигаться интенсивнее — это проявляется в виде нагрева тела. При сжатии пружины изменяется потенциальная энергия частиц.
Натянутая резинка обладает потенциальной энергией, причиной этого является взаимное притяжение молекул.
Закон сохранения энергии:
энергия не исчезает и не возникает снова, она только преобразуется из одного вида энергии в другой вид энергии или переходит от одного тела к другому.
Полная энергия тела — это сумма его механической и внутренней энергии.
Полная энергия тела
↗↖
Механическая энергия Внутренняя энергия
↗↖↗↖
Тела Eпот Тела Eкин Частиц Eпот Частиц Eкин
Источник
Найдем, чему равна работа
, совершаемая некоторой силой
при подъеме тела массы
на высоту
. Будем считать, что движение тела происходит медленно и что силами трения можно пренебречь. Мы знаем (§ 94), что работа против силы тяжести не зависит от того, как мы поднимаем тело: по вертикали (как гирю в часах), по наклонной плоскости (как при втаскивании сапок в гору) или еще каким-либо способом. Во всех случаях работа
. При опускании тела на первоначальный уровень сила тяжести произведет такую же работу, какая была затрачена силой
на подъем тела. Значит, поднимая тело, мы запасли работу, равную
, т. е. поднятое тело обладает энергией, равной произведению силы тяжести, действующей на это тело, и высоты, на которую оно поднято. Эта энергия не зависит от того, по какому пути происходил подъем, а определяется лишь положением тела (высотой на которую оно поднято) и называется потенциальной энергией. Итак, потенциальная энергия
тела, поднятого на некоторую высоту, выражается формулой
. (97.1)
При данном исходном положении тела работа, которую может совершить тело, т. е. его потенциальная энергия, зависит от того, насколько тело может опуститься. В гиревом механизме часов это определяется длиной цепочки, на которой висит гиря, в примере с наклонной плоскостью — высотой наивысшей точки наклонной плоскости над ее наинизшей точкой. В других случаях наинизший уровень не может быть так естественно определен. Например, если тело лежит на столе, то можно определять его потенциальную энергию той работой, которую оно совершило бы, опускаясь до пола, до уровня земли или до дна погреба и т. д. Поэтому нужно условиться заранее, от какого уровня отсчитывать высоту, а вместе с тем и потенциальную энергию тела. Выбрать этот уровень можно совершенно произвольно, так как во всех физических явлениях всегда бывает важна не сама потенциальная энергия, а ее изменение, которым определяется совершаемая работа. Изменение же потенциальной энергии будет, очевидно, одним и тем же, какой бы мы ни выбрали исходный уровень.
Если не оговорено противное, мы будем считать потенциальную энергию тела, лежащего на поверхности земли, равной нулю. Тогда в формуле (97.1) в качестве
следует брать высоту тела над поверхностью земли. Если тело имеет значительные размеры, то под
в формуле (97.1) нужно понимать расстояние от поверхности земли (или от иного нулевого уровня) до центра тяжести тела.
Рис. 164. При переходе столба из положения
в положение
; сила тяжести не совершает работы, так как центр тяжести тела остается на месте. При переходе из положения
в положение
совершается работа
Определим, например, на сколько потенциальная энергия вертикально стоящего столба (рис. 164, положение
) больше потенциальной энергии того же столба, лежащего на земле (положение
). Представим себе, что столб переходит из положения
в положение
в два приема. Сначала он поворачивается вокруг центра тяжести (в данном случае около средней точки) в положение
. При этом верхняя часть столба опускается, а нижняя поднимается, и сила тяжести совершает над верхней частью столба положительную, а над нижней — равную ей отрицательную работу, и полная работа силы тяжести равна нулю. Только при переходе из положения
в положение
сила тяжести совершает положительную работу. Следовательно, потенциальная энергия стоящего на земле столба больше потенциальной энергии столба, лежащего на земле, на величину
, где
— масса столба и
— разность высот центра тяжести в положениях
и
.
При подсчете потенциальной энергии жидкости массы
, находящейся в цилиндрическом сосуде (рис. 165), следует взять высоту
центра тяжести жидкости
над нулевым уровнем, т. е. высоту
дна сосуда над нулевым уровнем, плюс половину высоты уровня жидкости в сосуде
, так что потенциальная энергия
.
Рис. 165. к расчету потенциальной энергии жидкости в сосуде
97.1.
Ящик массы 40 кг, размеры которого показаны на рис. 166, переведен из положения а) в положение б). Определите приращение потенциальной энергии ящика, считая, что его центр тяжести лежит на пересечении диагоналей.
Рис. 166. К упражнению 97.1
97.2.
Водохранилище при гидростанции имеет цилиндрическую форму: его площадь равна
, глубина равна 6 м. Дно водохранилища лежит на высоте 12 м над уровнем воды в отводном канале за гидростанцией. Какова потенциальная энергия воды в хранилище?
Источник

1. Камень, упав с некоторой высоты на Землю, оставляет на поверхности Земли вмятину. Во время падения он совершает работу по преодолению сопротивления воздуха, а после касания земли — работу по преодолению силы сопротивления почвы, поскольку обладает энергией. Если накачивать в закрытую пробкой банку воздух, то при некотором давлении воздуха пробка вылетит из банки, при этом воздух совершит работу по преодолению трения пробки о горло банки, благодаря тому, что воздух обладает энергией. Таким образом, тело может совершить работу, если оно обладает энергией. Энергию обозначают буквой ( E ). Единица работы — ( [E,] ) = 1 Дж.
При совершении работы изменяется состояние тела и изменяется его энергия. Изменение энергии равно совершенной работе: ( E=A ).
2. Потенциальной энергией называют энергию взаимодействия тел или частей тела, зависящую от их взаимного положения.
Поскольку тела взаимодействуют с Землёй, то они обладают потенциальной энергия взаимодействия с Землёй.
Если тело массой ( m ) падает с высоты ( h_1 ) до высоты ( h_2 ), то работа силы тяжести ( F_т ) на участке ( h=h_1-h_2 ) равна: ( A = F_тh = mgh = mg(h_1 — h_2) ) или ( A = mgh_1 — mgh_2 ) (рис. 48).
В полученной формуле ( mgh_1 ) характеризует начальное положение (состояние) тела, ( mgh_2 ) характеризует конечное положение (состояние) тела. Величина ( mgh_1=E_{п1} ) — потенциальная энергия тела в начальном состоянии; величина ( mgh_2=E_{п2} ) — потенциальная энергия тела в конечном состоянии.
Можно записать ( A=E_{п1}-E_{п2} ), или ( A=-(E_{п2}-E_{п1}) ), или ( A=-E_{п} ).
Таким образом, работа силы тяжести равна изменению потенциальной энергии тела. Знак «–» означает, что при движении тела вниз и соответственно при совершении силой тяжести положительной работы потенциальная энергия тела уменьшается. Если тело поднимается вверх, то работа силы тяжести отрицательна, а потенциальная энергия тела увеличивается.
Если тело находится на некоторой высоте ( h ) относительно поверхности Земли, то его потенциальная энергия в данном состоянии равна ( E_п=mgh ). Значение потенциальной энергии зависит от того, относительно какого уровня она отсчитывается. Уровень, на котором потенциальная энергия равна нулю, называют нулевым уровнем.
В отличие от кинетической энергии потенциальной энергией обладают покоящиеся тела. Поскольку потенциальная энергия — это энергия взаимодействия, то она относится не к одному телу, а к системе взаимодействующих тел. В данном случае эту систему составляют Земля и поднятое над ней тело.
3. Потенциальной энергией обладают упруго деформированные тела. Предположим, что левый конец пружины закреплён, а к правому её концу прикреплён груз. Если пружину сжать, сместив правый её конец на ( x_1 ), то в пружине возникнет сила упругости ( F_{упр1} ), направленная вправо (рис. 49).
Если теперь предоставить пружину самой себе, то её правый конец переместится, удлинение пружины будет равно ( x_2 ), а сила упругости ( F_{упр2} ).
Работа силы упругости равна
[ A=F_{ср}(x_1-x_2)=k/2(x_1+x_2)(x_1-x_2)=kx_1^2/2-kx_2^2/2 ]
( kx_1^2/2=E_{п1} ) — потенциальная энергия пружины в начальном состоянии, ( kx_2^2/2=E_{п2} ) — потенциальная энергия пружины во конечном состоянии. Работа силы упругости равна изменению потенциальной энергии пружины.
Можно записать ( A=E_{п1}-E_{п2} ), или ( A=-(E_{п2}-E_{п1}) ), или ( A=-E_{п} ).
Знак «–» показывает, что при растяжении и сжатии пружины сила упругости совершает отрицательную работу, потенциальная энергия пружины увеличивается, а при движении пружины к положению равновесия сила упругости совершает положительную работа, а потенциальная энергия уменьшается.
Если пружина деформирована и её витки смещены относительно положения равновесия на расстояние ( x ), то потенциальная энергия пружины в данном состоянии равна ( E_п=kx^2/2 ).
4. Движущиеся тела так же могут совершить работу. Например, движущийся поршень сжимает находящийся в цилиндре газ, движущийся снаряд пробивает мишень и т.п. Следовательно, движущиеся тела обладают энергией. Энергия, которой обладает движущееся тело, называется кинетической энергией. Кинетическая энергия ( E_к ) зависит от массы тела и его скорости ( E_к=mv^2/2 ). Это следует из преобразования формулы работы.
Работа ( A=FS ). Сила ( F=ma ). Подставив это выражение в формулу работы, получим ( A=maS ). Так как ( 2aS=v^2_2-v^2_1 ), то ( A=m(v^2_2-v^2_1)/2 ) или ( A=mv^2_2/2-mv^2_1/2 ), где ( mv^2_1/2=E_{к1} ) — кинетическая энергия тела в первом состоянии, ( mv^2_2/2=E_{к2} ) — кинетическая энергия тела во втором состоянии. Таким образом, работа силы равна изменению кинетической энергии тела: ( A=E_{к2}-E_{к1} ), или ( A=E_к ). Это утверждение — теорема о кинетической энергии.
Если сила совершает положительную работу, то кинетическая энергия тела увеличивается, если работа силы отрицательная, то кинетическая энергия тела уменьшается.
5. Полная механическая энергия ( E ) тела — физическая величина, равная сумме его потенциальной ( E_п ) и кинетической ( E_п ) энергии: ( E=E_п+E_к ).
Пусть тело падает вертикально вниз и в точке А находится на высоте ( h_1 ) относительно поверхности Земли и имеет скорость ( v_1 ) (рис. 50). В точке В высота тела ( h_2 ) и скорость ( v_2 ) Соответственно в точке А тело обладает потенциальной энергией ( E_{п1} ) и кинетической энергией ( E_{к1} ), а в точке В — потенциальной энергией ( E_{п2} ) и кинетической энергией ( E_{к2} ).
При перемещении тела из точки А в точку В сила тяжести совершает работу, равную А. Как было показано, ( A=-(E_{п2}-E_{п1}) ), а также ( A=E_{к2}-E_{к1} ). Приравняв правые части этих равенств, получаем: ( -(E_{п2}-E_{п1})=E_{к2}-E_{к1} ), откуда ( E_{к1}+E_{п1}=E_{п2}+E_{к2} ) или ( E_1=E_2 ).
Это равенство выражает закон сохранения механической энергии: полная механическая энергия замкнутой системы тел, между которыми действуют консервативные силы (силы тяготения или упругости) сохраняется.
В реальных системах действуют силы трения, которые не являются консервативными, поэтому в таких системах полная механическая энергия не сохраняется, она превращается во внутреннюю энергию.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Два тела находятся на одной и той же высоте над поверхностью Земли. Масса одного тела ( m_1 ) в три раза больше массы другого тела ( m_2 ). Относительно поверхности Земли потенциальная энергия
1) первого тела в 3 раза больше потенциальной энергии второго тела
2) второго тела в 3 раза больше потенциальной энергии первого тела
3) первого тела в 9 раз больше потенциальной энергии второго тела
4) второго тела в 9 раз больше потенциальной энергии первого тела
2. Сравните потенциальную энергию мяча на полюсе ( E_п ) Земли и на широте Москвы ( E_м ), если он находится на одинаковой высоте относительно поверхности Земли.
1) ( E_п=E_м )
2) ( E_п>E_м )
3) ( E_п<E_м )
4) ( E_пgeq E_м )
3. Тело брошено вертикально вверх. Его потенциальная энергия
1) одинакова в любые моменты движения тела
2) максимальна в момент начала движения
3) максимальна в верхней точке траектории
4) минимальна в верхней точке траектории
4. Как изменится потенциальная энергия пружины, если её удлинение уменьшить в 4 раза?
1) увеличится в 4 раза
2) увеличится в 16 раз
3) уменьшится в 4 раза
4) уменьшится в 16 раз
5. Лежащее на столе высотой 1 м яблоко массой 150 г подняли относительно стола на 10 см. Чему стала равной потенциальная энергия яблока относительно пола?
1) 0,15 Дж
2) 0,165 Дж
3) 1,5 Дж
4) 1,65 Дж
6. Скорость движущегося тела уменьшилась в 4 раза. При этом его кинетическая энергия
1) увеличилась в 16 раз
2) уменьшилась в 16 раз
3) увеличилась в 4 раза
4) уменьшилась в 4 раза
7. Два тела движутся с одинаковыми скоростями. Масса второго тела в 3 раза больше массы первого. При этом кинетическая энергия второго тела
1) больше в 9 раз
2) меньше в 9 раз
3) больше в 3 раза
4) меньше в 3 раза
8. Тело падает на пол с поверхности демонстрационного стола учителя. (Сопротивление воздуха не учитывать.) Кинетическая энергия тела
1) минимальна в момент достижения поверхности пола
2) минимальна в момент начала движения
3) одинакова в любые моменты движения тела
4) максимальна в момент начала движения
9. Книга, упавшая со стола на пол, обладала в момент касания пола кинетической энергией 2,4 Дж. Высота стола 1,2 м. Чему равна масса книги? Сопротивлением воздуха пренебречь.
1) 0,2 кг
2) 0,288 кг
3) 2,0 кг
4) 2,28 кг
10. С какой скоростью следует бросить тело массой 200 г с поверхности Земли вертикально вверх, чтобы его потенциальная энергия в наивысшей точке движения была равна 0,9 Дж? Сопротивлением воздуха пренебречь. Потенциальную энергию тела отсчитывать от поверхности земли.
1) 0,9 м/с
2) 3,0 м/с
3) 4,5 м/с
4) 9,0 м/с
11. Установите соответствие между физической величиной (левый столбец) и формулой, по которой она вычисляется (правый столбец). В ответе запишите подряд номера выбранных ответов
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия взаимодействия тела с Землёй
Б. Кинетическая энергия
B. Потенциальная энергия упругой деформации
ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) ( E=mv^2/2 )
2) ( E=kx^2/2 )
3) ( E=mgh )
12. Мяч бросили вертикально вверх. Установите соответствие между энергией мяча (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия
Б. Кинетическая энергия
B. Полная механическая энергия
ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) Уменьшается
2) Увеличивается
3) Не изменяется
Часть 2
13. Пуля массой 10 г, движущаяся со скоростью 700 м/с, пробила доску толщиной 2,5 см и при выходе из доски имела скорость 300 м/с. Определить среднюю силу сопротивления, воздействующую на пулю в доске.
Ответы
Потенциальная и кинетическая энергия. Закон сохранения механической энергии
3.3 (65%) 12 votes
Источник
