Как найти среднюю полезную мощность формула
Определение и формула полезной мощности
Определение
Мощность – это физическая величина, которую использует как основную характеристику любого устройства, которое применяют
для совершения работы. Полезная мощность может быть использована для выполнения поставленной задачи.
Отношение работы ($Delta A$) к промежутку времени за которое она выполнена ($Delta t$) называют средней мощностью ($leftlangle Prightrangle $) за это время:
[leftlangle Prightrangle =frac{Delta A}{Delta t}left(1right).]
Мгновенной мощностью или чаще просто мощностью называют предел отношения (1) при $Delta tto 0$:
[P={mathop{lim }_{Delta tto 0} frac{Delta A}{Delta t} }=A'(t)left(2right).]
Приняв во внимание, что:
[Delta A=overline{F}cdot Delta overline{r }left(3right),]
где $Delta overline{r }$ – перемещение тела под действием силы $overline{F}$, в выражении (2) имеем:
[P={mathop{lim }_{Delta tto 0} left(frac{overline{F}cdot Delta overline{r }}{Delta t}right) }=overline{F}{mathop{lim }_{Delta tto 0} left(frac{Delta overline{r }}{Delta t}right)= }overline{F}cdot overline{v}left(4right),]
где $ overline{v}-$ мгновенная скорость.
Коэффициент полезного действия
При выполнении необходимой (полезной) работы, например, механической, приходится выполнять работу большую по величине, так как в реальности существуют силы сопротивления и часть энергии подвержена диссипации (рассеиванию). Эффективность совершения работы определяется при помощи коэффициента полезного действия ($eta $), при этом:
[eta =frac{P_p}{P}left(5right),]
где $P_p$ – полезная мощность; $P$ – затраченная мощность. Из выражения (5) следует, что полезная мощность может быть найдена как:
[P_p=eta P left(6right).]
Формула полезной мощности источника тока
Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:
[P=?I left(7right),]
где $?$ – ЭДС источника тока; $I$ – сила тока. При этом $P$ – полная мощность цепи.
Обозначим $U$ – напряжение на внешнем участке цепи, тогда формулу (7) представим в виде:
[P=?I=UI+I^2r=P_p+P_0left(8right),]
где $P_p=UI=I^2R=frac{U^2}{R}(9)$ – полезная мощность; $P_0=I^2r$ – мощность потерь. При этом КПД источника определяют как:
[eta =frac{P_p}{P_p+P_0}left(9right).]
Максимальную полезную мощность (мощность на нагрузке) электрический ток дает, если внешнее сопротивление цепи будет равно внутреннему сопротивлению источника тока. При этом условии полезная мощность равна 50% общей мощности.
При коротком замыкании (когда $Rto 0;;Uto 0$) или в режиме холостого хода $(Rto infty ;;Ito 0$) полезная мощность равна нулю.
Примеры задач с решением
Пример 1
Задание. Коэффициент полезного действия электрического двигателя равен $eta $ =42%. Какой будет его полезная мощность, если при напряжении $U=$110 В через двигатель идет ток силой $I=$10 А?
Решение. За основу решения задачи примем формулу:
[P_p=eta P left(1.1right).]
Полную мощность найдем, используя выражение:
[P=IUleft(1.2right).]
Подставляя правую часть выражения (1.2) в (1.1) находим, что:
[P_p=eta IU.]
Вычислим искомую мощность:
[P_p=eta IU=0,42cdot 110cdot 10=462 left(Втright).]
Ответ. $P_p=462$ Вт
Пример 2
Задание. Какова максимальная полезная мощность источника тока, если ток короткого замыкания его
равен $I_k$? При соединении с источником тока сопротивления $R$, по цепи (рис.1) идет ток силой $I$.
Решение. По закону Ома для цепи с источником тока мы имеем:
[I=frac{varepsilon}{R+r}left(2.1right),]
где $varepsilon$ – ЭДС источника тока; $r$ – его внутреннее сопротивление.
При коротком замыкании считаем, что сопротивление внешней нагрузки равно нулю ($R=0$), тогда сила тока короткого замыкания равна:
[I_k=frac{varepsilon}{r} left(2.2right).]
Максимальная полезная мощность в цепи рис.1 электрический ток даст, при условии:
[R=r left(2.3right).]
Тогда сила тока в цепи равна:
[I’=frac{varepsilon}{r+r}=frac{varepsilon}{2r}left(2.4right).]
Максимальную полезную мощность найдем, используя формулу:
[P_{p max}={I’}^2r={left(frac{varepsilon}{2r}right)}^2cdot r=frac{varepsilon^2}{4r}=frac{varepsilon^2}{4R}left(2.5right).]
Мы получили систему из трех уравнений с тремя неизвестными:
[left{ begin{array}{c}
I’=frac{varepsilon}{2r}, \
I_k=frac{varepsilon}{r}, \
P_{p max}={left(I’right)}^2r end{array}
left(2.6right).right.]
Используя первое и второе уравнения системы (2.6) найдем $I’$:
[frac{I’}{I_k}=frac{varepsilon}{2r}cdot frac{r}{varepsilon}=frac{1}{2}to I’=frac{1}{2}I_kleft(2.7right).]
Используем уравнения (2.1) и (2.2) выразим внутреннее сопротивление источника тока:
[varepsilon=Ileft(R+rright);; I_kr=varepsilon to Ileft(R+rright)=I_krto rleft(I_k+Iright)=IRto r=frac{IR}{I_k-I}left(2.8right).]
Подставим результаты из (2.7) и (2.8) в третью формулу системы (2.6), искомая мощность будет равна:
[P_{p max}={left(frac{1}{2}I_kright)}^2frac{IR}{I_k-I}.]
Ответ. $P_{p max}={left(frac{1}{2}I_kright)}^2frac{IR}{I_k-I}$
Читать дальше: формула равнодействующей всех сил.
Источник
3.3. Работа и мощность механической системы
3.3.2. Мощность
Скорость совершения работы характеризуется мощностью.
Различают среднюю и мгновенную мощность.
Средняя мощность определяется формулой
〈N〉=AΔt,
где A — работа, совершаемая за время ∆t.
Для вычисления средней мощности также пользуются формулой
N=(F→,〈v→〉)=F→⋅〈v→〉=F〈v〉cosα,
где F→ — сила, совершающая работу; 〈v→〉 — средняя скорость перемещения; α — угол между векторами F→ и 〈v→〉.
В Международной системе единиц мощность измеряется в ваттах (1 Вт).
Мгновенная мощность определяется формулой
N = A′(t),
где A′(t) — производная от функции работы по времени.
Для вычисления мгновенной мощности также пользуются формулой
N=(F→,v→)=F→⋅v→=Fvcosα,
где F→ — сила, совершающая работу; v→ — мгновенная скорость перемещения; α — угол между векторами F→ и v→.
Пример 20. Тело массой 60 г к моменту падения на Землю имеет скорость 5,0 м/с. Определить мощность силы тяжести в этот момент.
Решение. На рисунке показаны направления скорости тела и силы тяжести, действующей на тело.
В задаче задана мгновенная скорость тела; следовательно, мощность, которую необходимо рассчитать, также является мгновенной мощностью. Величина мгновенной мощности силы тяжести определяется формулой
N = mgv cos α,
где mg — модуль силы тяжести; m — масса тела; g — модуль ускорения свободного падения; v — модуль скорости тела; α = 0° — угол между векторами скорости и силы.
Произведем вычисление:
N=60⋅10−3⋅10⋅5,0⋅1=3,0 Вт.
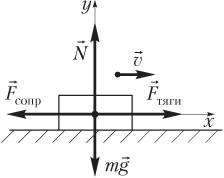
Пример 21. При скорости 36 км/ч мощность двигателя автомобиля равна 2,0 кВт. Считая, что сила сопротивления движению автомобиля со стороны воздуха и дороги пропорциональна квадрату скорости, определить мощность двигателя при скорости 72 км/ч.
Решение. Мощность двигателя автомобиля определяется силой тяги и скоростью:
N*=Fтягиvcosα,
где Fтяги — величина силы тяги двигателя автомобиля; v — модуль скорости автомобиля при заданной мощности; α = 0° — угол между векторами силы тяги и скорости.
Силы, действующие на автомобиль, направление его скорости и выбранная система координат показаны на рисунке.
Для определения величины силы тяги запишем второй закон Ньютона с учетом того, что автомобиль движется с постоянной скоростью:
F→тяги+F→сопр+mg→+N→=0,
или в проекциях на координатные оси —
Ox: Fтяги−Fсопр=0;Oy: N−mg=0,}
где Fсопр — модуль силы сопротивления движению автомобиля; N — модуль силы нормальной реакции, действующей на автомобиль со стороны дороги; m — масса автомобиля; g — модуль ускорения свободного падения.
Из первого уравнения системы следует равенство модулей сил тяги и сопротивления:
Fтяги = Fсопр.
По условию задачи сила сопротивления пропорциональна квадрату скорости автомобиля:
Fсопр = kv2,
где k — коэффициент пропорциональности.
Подстановка данного выражения в формулу для силы тяги
Fтяги = kv2,
а затем в формулу для вычисления мощности дает:
N*=kv3cosα.
Таким образом, мощность двигателя автомобиля определяется формулой:
- при скорости v1 —
N1*=kv13cosα;
- при скорости v2 —
N2*=kv23cosα,
где v1 = 36 км/ч — первая скорость автомобиля; v2 = 72 км/ч — вторая скорость автомобиля.
Отношение
N1*N2*=kv13cosαkv23cosα=(v1v2)3
позволяет вычислить искомую мощность автомобиля:
N2*=N1*(v2v1)3=2,0⋅103⋅(7236)3=16⋅103 Вт=16 кВт.
Пример 22. Два автомобиля одновременно трогаются с места и движутся равноускоренно. Массы автомобилей одинаковы. Во сколько раз средняя мощность первого автомобиля больше средней мощности второго, если за одно и то же время первый автомобиль развивает скорость вдвое большую, чем второй? Сопротивлением движению пренебречь.
Решение. Мощность двигателей автомобилей определяется формулой:
- для первого автомобиля
N1*=Fтяги1v1cosα,
- для второго автомобиля
N2*=Fтяги2v2cosα,
где Fтяги1 — величина силы тяги двигателя первого автомобиля; v1 — модуль скорости первого автомобиля; Fтяги2 — величина силы тяги двигателя второго автомобиля; v2 — модуль скорости второго автомобиля; α = 0° — угол между векторами силы тяги и скорости.
Силы, действующие на первый и второй автомобиль, направление движения и выбранная система координат показаны на рисунке.
Для определения величины силы тяги запишем второй закон Ньютона с учетом того, что автомобили движутся равноускоренно:
- для первого автомобиля
F→тяги1+m1g→+N→1=m1a→1,
или в проекциях на координатные оси —
Ox: Fтяги1=m1a1;Oy: N1−m1g=0,}
- для второго автомобиля
F→тяги2+m2g→+N→2=m2a→2,
или в проекциях на координатные оси —
Ox: Fтяги2=m2a2;Oy: N2−m2g=0,}
где m1 — масса первого автомобиля; m2 — масса второго автомобиля; g — модуль ускорения свободного падения; N1 — модуль силы нормальной реакции, действующей на первый автомобиль со стороны дороги; N2 — модуль силы нормальной реакции, действующей на второй автомобиль со стороны дороги; a1 — модуль ускорения первого автомобиля; a2 — модуль ускорения второго автомобиля.
Из записанных уравнений следует, что величины сил тяги первого и второго автомобиля определяются формулами:
- для первого автомобиля
Fтяги1 = m1a1,
- для второго автомобиля
Fтяги2 = m2a2.
Отношение модулей сил тяги (Fтяги1/Fтяги2) определяется отношением
Fтяги1Fтяги2=m1a1m2a2.
Движение автомобилей происходит равноускоренно без начальной скорости, поэтому их скорость с течением времени изменяется по законам:
- для первого автомобиля
v1 = a1t,
- для второго автомобиля
v2 = a2t,
где t — время.
Отношение модулей скоростей (v1/v2) определяется отношением величин ускорений (a1/a2):
v1v2=a1a2,
а отношение мощностей —
N1*N2*=Fтяги1v1cosαFтяги2v2cosα=Fтяги1Fтяги2v1v2.
Подставим в полученное отношение выражения для (Fтяги1/Fтяги2) и (v1/v2):
N1*N2*=m1a1m2a2a1a2=m1m2(a1a2)2.
Преобразование формулы с учетом равенства масс автомобилей (m1 = m2 = m) и замены (a1/a2 = v1/v2) дает искомое отношение мощностей:
N1*N2*=(v1v2)2=(2v2v2)2=22=4.
Таким образом, мощность первого автомобиля в 4 раза больше мощности второго автомобиля.
Источник
Мощность по своей сути является скоростью выполнения работы. Чем больше мощность совершаемой работы, тем больше работы выполняется за единицу времени.
Среднее значение мощности — это работа, выполненная за единицу времени.
Величина мощности прямо пропорциональна величине совершённой работы (A) и обратно пропорциональна времени (t), за которое работа была совершена.
Мощность (N) определяют по формуле:
N=At.
Единицей измерения мощности в системе (СИ) является (Ватт) (русское обозначение — (Вт), международное — (W)).
Для определения мощности двигателя автомобилей и других транспортных средств используют исторически более древнюю единицу измерения — лошадиная сила (л.с.), 1 л.с. = 736 Вт.
Пример:
Мощность двигателя автомобиля равна примерно (90 л.с. = 66240 Вт).
Мощность автомобиля или другого транспортного средства можно рассчитать, если известна сила тяги автомобиля (F) и скорость его движения (v).
N=F⋅v
Эту формулу получают, преобразуя основную формулу определения мощности.
Ни одно устройство не способно использовать (100) % от начально подведённой к нему энергии на совершение полезной работы. Поэтому важной характеристикой любого устройства является не только мощность, но и коэффициент полезного действия, который показывает, насколько эффективно используется энергия, подведённая к устройству.
Пример:
Для того чтобы автомобиль двигался, должны вращаться колёса. А для того чтобы вращались колёса, двигатель должен приводить в движение кривошипно-шатунный механизм (механизм, который возвратно-поступательное движение поршня двигателя преобразует во вращательное движение колёс). При этом приводятся во вращение шестерни и большая часть энергии выделяется в виде тепла в окружающее пространство, в результате чего происходит потеря подводимой энергии. Коэффициент полезного действия двигателя автомобиля находится в пределах (40 — 45) %. Таким образом, получается, что только около (40) % от всего бензина, которым заправляют автомобиль, идёт на совершение необходимой нам полезной работы — перемещение автомобиля.
Если мы заправим в бак автомобиля (20) литров бензина, тогда только (8) литров будут расходоваться на перемещение автомобиля, а (12) литров сгорят без совершения полезной работы.
Коэффициент полезного действия обозначается буквой греческого алфавита («эта») η, он является отношением полезной мощности (N) к полной или общей мощности Nполная.
Для его определения используют формулу: η=NNполная. Поскольку по определению коэффициент полезного действия является отношением мощностей, единицы измерения он не имеет.
Часто его выражают в процентах. Если коэффициент полезного действия выражают в процентах, тогда используют формулу: η=NNполная⋅100%.
Так как мощность является работой, проделанной за единицу времени, тогда коэффициент полезного действия можно выразить как отношение полезной проделанной работы (A) к общей или полной проделанной работе Aполная. В этом случае формула для определения коэффициента полезного действия будет выглядеть так:
η=AAполная⋅100%.
Коэффициент полезного действия всегда меньше (1), или (100) % (η < 1, или η < (100) %).
Источники:
E. Šilters, V. Regusts, A. Cābelis. «Fizika 10. klasei», Lielvārds, 2004, 256 lpp.
(Э. Шилтерс, В. Регустс, А. Цабелис. «Физика для 10 класса», Lielvārds, 2004, 256 стр.)
Источник
Мощность, развиваемая источником тока во всей цепи, называется полной мощностью.
Она определяется по формуле
где Pоб-полная мощность, развиваемая источником тока во всей цепи, вт;
Е- э. д. с. источника, в;
I-величина тока в цепи, а.
В общем виде электрическая цепь состоит из внешнего участка (нагрузки) с сопротивлением R и внутреннего участка с сопротивлением R0 (сопротивлением источника тока).
Заменяя в выражении полной мощности величину э. д. с. через напряжения на участках цепи, получим
Величина UI соответствует мощности, развиваемой на внешнем участке цепи (нагрузке), и называется полезной мощностью Pпол=UI.
Величина UoI соответствует мощности, бесполезно расходуемой внутри источника, Ее называют мощностью потерь Po=UoI.
Таким образом, полная мощность равна сумме полезной мощности и мощности потерь Pоб=Pпол+P0.
Отношение полезной мощности к полной мощности, развиваемой источником, называется коэффициентом полезного действия, сокращенно к. п. д.,и обозначается η.
Из определения следует
При любых условиях коэффициент полезного действия η ≤ 1.
Если выразить мощности через величину тока и сопротивления участков цепи, получим
Таким образом, к. п. д. зависит от соотношения между внутренним сопротивлением источника и сопротивлением потребителя.
Обычно электрический к. п. д. принято выражать в процентах.
Для практической электротехники особый интерес представляют два вопроса:
1. Условие получения наибольшей полезной мощности
2. Условие получения наибольшего к. п. д.
Наибольшую полезную мощность( мощность на нагрузке) электрический ток развивает в том случае, если сопротивление нагрузки равно сопротивлению источника тока.
Эта наибольшая мощность равна половине всей мощности (50%) развиваемой источником тока во всей цепи.
Половина мощности развивается на нагрузке и половина развивается на внутреннем сопротивлении источника тока.
Если будем уменьшать сопротивление нагрузки, то мощность развиваемая на нагрузке будет уменьшаться а мощность развиваемая на внутреннем сопротивлении источника тока будет увеличиваться.
Если сопротивление нагрузки равно нулю то ток в цепи будет максимальным, это режим короткого замыкания (КЗ). Почти вся мощность будет развивается на внутреннем сопротивлении источника тока. Этот режим опасен для источника тока а также для всей цепи.
Если сопротивление нагрузки будем увеличивать, то ток в цепи будет уменьшатся, мощность на нагрузке также будет уменьшатся. При очень большом сопротивлении нагрузки тока в цепи вообще не будет. Это сопротивление называется бесконечно большим. Если цепь разомкнута то ее сопротивление бесконечно большое. Такой режим называется режимом холостого хода.
Таким образом, в режимах, близких к короткому замыканию и к холостому ходу, полезная мощность мала в первом случае за счет малой величины напряжения, а во втором за счет малой величины тока.
Коэффициент полезного действия (к. п. д.) равен 100% при холостом ходе ( в этом случае полезная мощность не выделяется, но в то же время и не затрачивается мощность источника).
По мере увеличения тока нагрузки к. п. д. уменьшается по прямолинейному закону.
В режиме короткого замыкания к. п. д. равен нулю ( полезной мощности нет, а мощность развиваемая источником, полностью расходуется внутри него).
Подводя итоги вышеизложенному, можно сделать выводы.
Условие получения максимальной полезной мощности( R=R0) и условие получения максимального к. п. д. (R=∞) не совпадают. Более того, при получении от источника максимальной полезной мощности ( режим согласованной нагрузки) к. п. д.составляет 50%, т.е. половина развиваемой источником мощности бесполезно затрачивается внутри него.
В мощных электрических установках режим согласованной нагрузки является неприемлемым, так как при этом происходит бесполезная затрата больших мощностей. Поэтому для электрических станций и подстанций режимы работы генераторов, трансформаторов, выпрямителей рассчитываются так, чтобы обеспечивался высокий к. п. д. ( 90% и более).
Иначе обстоит дело в технике слабых токов. Возьмем, например, телефонный аппарат. При разговоре перед микрофоном в схеме аппарата создается электрический сигнал мощностью около 2 мвт. Очевидно, что для получения наибольшей дальности связи необходимо передать в линию как можно большую мощность, а для этого требуется выполнить режим согласованного включения нагрузки. Имеет ли в данном случае существенное значение к. п. д.? Конечно нет, так как потери энергии исчисляются долями или единицами милливатт.
Режим согласованной нагрузки применяется в радиоаппаратуре. В том случае, когда согласованный режим при непосредственном соединении генератора и нагрузки не обеспечивается, применяют меры согласования их сопротивлений.
Источник

