Как найти а полезное и затраченное

Механическая работа – это одна из основных скалярных величин в физике. В рамках стандартной школьной программы она изучается в седьмом классе в разделе механики. Механическая работа – один из способов изменения внутренней энергии тела или субстанции (например, газа или жидкости) наряду с такими формами теплопередачи, как теплопроводность, конвекция и излучение, которые изучаются в разделе тепловых явлений.

Что такое работа в физике – определение и формула

Механическая работа – это количество энергии, которое нужно затратить для того, чтобы тело начало равномерно замедляющееся движение и прошло некоторую дистанцию. 

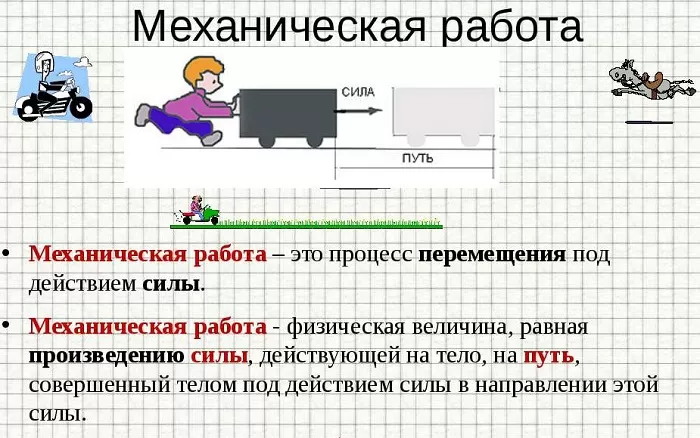
В физике механической работой называется произведение силы, которая действует на некоторое тело, на расстояние, которое оно проходит под ее воздействием:

A = F * S

В более сложных случаях в формуле появляется и третья величина – косинус угла, под которым друг к другу расположены векторы движения и приложенной силы. Найти ее значение можно по формуле:

A = F * S * cosA

В чем измеряется работа

Физические единицы, в которых выражается механическая работа, – Джоули. 

Существуют разные способы для ее практического измерения, которые зависят от типа произведенного движения. При этом в формулу работы подставляют значение силы в Ньютонах и расстояния в метрах. Угол между векторами измеряют в математических единицах – градусах. 

Работа силы трения

При условиях, существующих на Земле, на любое движущееся тело оказывает воздействие сила трения, замедляющая его движение. Чаще всего это трение поверхности, по которой движется объект. Это очевидно из того факта, что при воздействии постоянной силы на тело его скорость окажется переменной. 

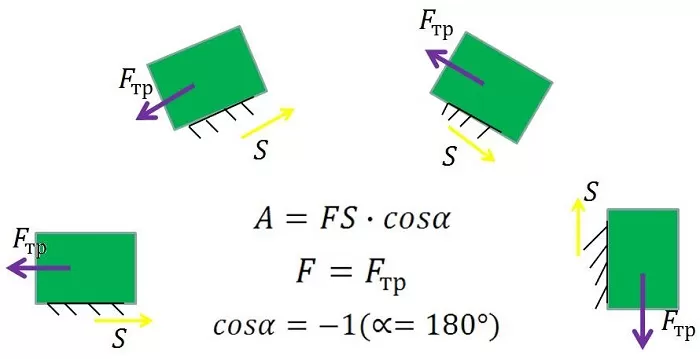
Следовательно, должна быть и другая сила, противодействующая ей – и это сила трения. Если система координат выбрана по направлению движения тела, то ее числовое значение будет отрицательным.

Положительная и отрицательная работа

Числовое значение работы, которую совершает сила, может становиться отрицательным в случае если ее вектор противоположен вектору скорости. 

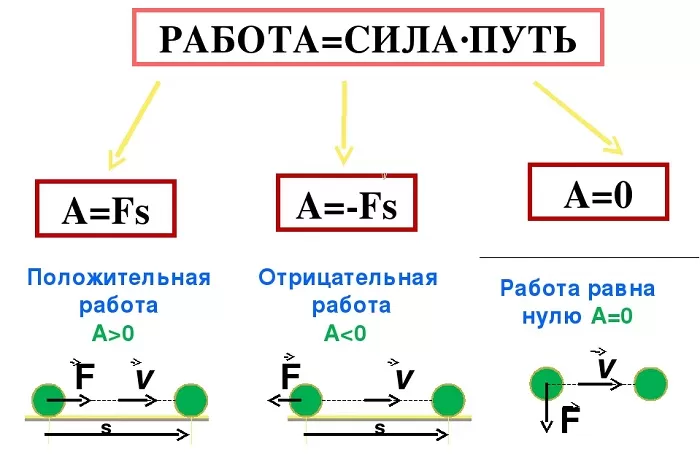
Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае она будет называться противодействующей. 

Полезная или затраченная работа

У тела, совершающего одно и то же действие, есть два значения работы. Первая из них, полезная, вычисляется по обычной формуле. 

Вторая, затраченная, по своему понятию не имеет общей формулы для вычисления и измеряется практически. Эта разница между совершенной в реальности работой и той, которая должна была быть совершена в теории, равна коэффициенту полезного действия – КПД. Он вычисляется так:

КПД = А полезная / А затраченная,

и выражается в процентах. КПД всегда меньше 100.

Мощность

Среднее количество работы, совершаемой за единицу времени (секунду), характеризует такую величину, как мощность. Формула для ее вычисления выглядит так:

Р = A / t

В качестве работы можно подставить люблю известную формулу для ее вычисления в зависимости от ситуации. Ответ будет выражен в Ваттах.

Однако при равномерном движении можно использовать и другую формулу:

Р = F * v

Подставив вместо обычной скорости мгновенную, можно получить значение мгновенной мощности.

Примеры решения задач

Рассмотрим несколько простых задач на нахождение механической работы.

Задача 1

Какую работу совершает подъемный механизм, поднимающий десятикилограммовый блок на высоту 50 метров.

Решение:

Для того, чтобы поднять тело, необходимо преодолеть действующую на него силу тяжести. То есть F, с которой поднимают блок, равна той, с которой он притягивается к земле. Так как последняя равна m * g, то для нахождения конечного результата понадобится только одна измененная версия стандартной формулы, упомянутой выше: A = S * m * g.

При помощи простой математики найдем числовой ответ:

A = 50 м * 10 кг * 10 Н/кг;

A = 5000 Дж.

Ответ: 5000 Дж.

Впрочем, не всегда речь идет о силе тяжести.

Задача 2

Какая работа совершается силой упругости, когда пружина с жесткостью 10 Н/м, сжатая на 20 см, возвращается в исходное состояние? Система замкнута, нет никаких внешних сил, воздействующих на пружину.

Решение:

Для начала нужно найти саму F упругости, которая совершает работу. Ее формула – F = x * |k|, где x – это длина, на которую сжимается или растягивается пружина, а k – коэффициент ее жесткости. Перемещение пружины равно ее деформации, и следовательно, конечная формула в этом случае будет выглядеть так: A = S * x * k = x * x * k = x^2 * k.

Далее при помощи элементарных вычислений рассчитаем ответ:

A = (0,2 м)^2 * 10 Н/м = 0,04 * 10 = 0,4 Дж.

Ответ: 0,4 Дж.

Но во всех задачах по данной теме траектория движения тела прямая.

Задача 3

Рассчитайте, какова сила, действующая на колесо, если на то, чтобы совершить полный оборот, ему требуется 10 кДж. Диаметр диска равен 40 см, а толщина шины – 10 см.

Решение:

В этом случае нам нужно найти не А, а F, но сделать это можно при помощи все той же формулы. Возьмем точку на поверхности колеса. Предположим, что при вращательном движении ее вектор будет противоположен вектору приложения силы, а значит косинусом в формуле вновь можно пренебречь. Таким образом, за один оборот колеса точка пройдет расстояние, равное длине окружности, которую можно вычислить как 2πr или πd. Диаметр окружности можно найти из предоставленных данных: он равен сумме диаметра диска и удвоенной толщины шины, то есть 40 см + 2 * 10 см = 40 см + 20 см = 60 см = 0,6 м.

Теперь, когда мы можем вычислить расстояние, у нас есть все данные для того, чтобы приступить к нахождению силы.

Формула работы для этого случая будет такой: A = F * π * d, то силу, соответственно, можно будет выразить как F = A / (π * d).

В таком случае:

F = 10 кДж / (3,14 * 0,6 м) = 10000 Дж / 1,884 м = ~ 5308 Н.

Ответ: 5308 Н.

В завершение решим самый сложный вариант задачи, включающий в себя все, о чем говорилось выше.

Задача 4

Автомобиль Фольксваген весом 2500 кг заезжает на гору. Какова должна быть его минимальная скорость, чтобы удержаться на горе, если сила тяги равна 10 кН, время работы двигателя – 10 с, КПД – 30%, а угол наклона горы – 60 градусов. Трением и прочими силами пренебречь.

Решение:

На первый взгляд задача может показаться сложной, но для ее решения используются только простые известные формулы. 

Запишем условие в более наглядном виде.

Дано:

m = 2500 кг;

F = 10000 H;

t = 10 с;

КПД = 30%;

угол A = 1500 (60+90, т. к. сила тяжести приложена под углом 90 к горизонтали);

V – ?

Выведение формулы:

Шаг 1. По условию A1 (силы тяжести) = А2 (тяги).

A1 = mg;

A2 = P * t / КПД.

То есть mg = P * t / КПД.

Шаг 2. P = F * V * cosA.

Шаг 3. Общая формула: mg = F * V * cosA * t / КПД.

V = (m * g * КПД) / (F * t * cosA).

Числовое решение:

V = (2500 кг * 10 Н/кг * 30%) / (10000 H * 10 с * cos150);

V = (2500 кг * 10 Н/кг * 0,3) / (10000 H * 10 с * cos60);

V = 7500 / 50000;

V = 0,15 м/с.

Ответ: 0,15 м/с.

Выбирая техническое устройство, всегда обращают внимание на эффективность его работы. Иными словами, насколько высока энергоэффективность. Получить ответ на этот вопрос можно, если произвести вычисление коэффициента его полезного действия. Тогда становится понятным, насколько затраченные усилия будут обеспечивать полезный результат работы.

Понятие КПД (коэффициента полезного действия)

Термин «КПД» широко используется не только среди профессионалов, но и в быту. Под ним понимают, насколько совершенная работа превышает полезную, т.е. ту, ради которой механизм или прибор приобретается.

Учеными разработана специальная формула, из которой следует, что КПД всегда меньше единицы. Чтобы рассчитать коэффициент, нужно полезную работу, выраженную в Джоулях, разделить на энергию, которая затрачена на эту работу. Поскольку энергия также выражается в Джоулях, конечная расчетная величина безразмерна.

Источник: mashintop.ru

Объяснить бытовым языком данное понятие можно так: энергия, выделяемая от плиты, на которой должен закипеть чайник, расходуется не только на его нагревание. Она должна нагреть саму посудину, воздух вокруг нее, сам нагревательный элемент. И только ее часть будет расходоваться на передачу воде. Чтобы сориентироваться, насколько долго будет закипать чайник одного объема на различного вида печах, нужно знать их КПД.

В поисках наиболее эффективного прибора не стоит стремиться к единице. Такого не бывает. Например, КПД атомной электростанции примерно равно 35%.

Происходит это по двум причинам:

1. Исходя из закона сохранения энергии, получить больше работы, чем затрачено энергии, невозможно.
2. Любая работа сопровождается определенными потерями, будь-то нагревание тары или преодоление сил трения при движении по поверхности.

Термин КПД применим практически к каждому процессу, в котором имеется затраченная и полезная работа.

Применение в различных сферах физики

Характеризуя КПД, следует учитывать, что он не является константой, поскольку в каждом случае свои особенности энергозатрат. С другой стороны, он не может быть установлен изолированно от конкретных процессов. Если рассмотреть работу электродвигателя, величина его КПД сложится исходя из преобразования энергии тока в механическую работу.

В данном случае КПД рассматривается не как соотношение полезной и общей работы, а как соотношение отдаваемой мощности и подводимой к рабочему механизму.

В формулу (η=P2/P1) должны быть включены P1 – первичная мощность и P2 – мощность прибора.

В качестве первого примера выведем формулу КПД для варианта определения с величинами работы и затраченной энергии (формула для определения КПД теплового двигателя). Условными обозначениями в ней будут являться:
Ап – работа полезная;

• Q1 – количество энергии (или тепла), полученной от нагревающего устройства;
• Q2 – количество энергии (или тепла), отданное в процессе деятельности;
• Q1 – Q2 – та энергия (или тепло), которая пошла на процесс.

В итоге получится выражение:

Теперь выразим формулу через соотношение мощностей. Условные обозначения следующие:

Ротд – полезная (эффективная) мощность;

Рподв – номинальная мощность.

Формула будет выглядеть так:

Если затрата или передача энергии происходит неоднократно, общий КПД равен сумме КПД на каждом участке процесса:

Какой буквой обозначается, единицы измерения

В вышеприведенной формуле искомая величина коэффициента полезного действия обозначается буквой η, которая произносится “эта”.

Для упрощения понимания величины, КПД чаще выражается в процентах.

Физическая формула КПД

С учетом изложенных выше особенностей и необходимости выражения результата в %, физические формулы приобретают усовершенствованный внешний вид:

или

Примеры расчета КПД

Формула применяется для расчетов коэффициентов машин различного типа.

Задача 1

Имеется 10 кг дров, теплота сгорания которых составляет 95 Дж/кг. При их сгорании в помещении объемом 75 м3 установилась температура 22оС (допускаем, что удельная теплоемкость воздуха равна 1,3 кДж/ кгхград).

Решение состоит из нескольких действий:

1. 1300 Дж умножить на 75 (объем) и 22 (температуру). Получаем 2 145 кДж. Это то тепло, выраженное в кДж, которое поступило в воздух помещения.
2. 10700000Дж умножаем на 10 (количество дров) =10х107 кДж.
3. При делении полезного тепла и полного, выработанного обогревателем, получаем значение 2,5%. Это говорит о низкой эффективности прибора и большой затрате дров и необходимости внесения конструктивных изменений, например, оборудования возможности дымоходам нагревать не только воздух, но и предметы в помещении.

Задача 2

В доме установлен электробойлер объемом 80 литров. Нагревательный элемент имеет мощность 2 кВт. Было замечено, что для нагревания воды от 12оС до 70оС уходит 3 часа. Нужно определить КПД прибора.

Дополнительные данные: плотность воды составляет 1000 кг/м3, ее теплоемкость – 4200 Дж/кг*оС.

Решать задачу нужно по формуле:

(eta=Q_{пол}div Q_{зат}times100%)

(Q_{зат}=Ntimes t=10800(сек))

(Q_{пол}=ctimes mtimes(T_2-T_1))

(m=rhotimes V)

(T_1=12) oC

(T_2=70) oC

Конечная формула:

(eta=(ctimesrhotimes Vtimes(T_2-T_1)div Ntimes t)times100%=90%)

Задача 3

Температура воды, налитой в котел паровой машины, составляет 160оС. Температура холодильника – 10оС. Коэффициент полезного действия машины – 60%. В топке сжигается 200 кг угля. Его удельная теплота сгорания – 2,9 • 107 Дж/кг. О какой максимальной работе может идти речь для данной машины?

Решение следующее. Амакс возможна для идеальной тепловой машины, которая функционирует по циклу Карно. Ее КПД равно (Т1-Т2)/Т1. В этой формуле Т1 и Т2 – температуры нагревателя, холодильника.

Определяем КПД, пользуясь формулой: ( eta;=;Adiv Q_1). В этой формуле А – работа тепловой машины, Q1 – теплота, полученная от нагревателя. С другой стороны, она равна (eta_1times mtimes q).

(Q_1;=;eta_1times mtimes q)

((T_1-T_2)div T_1=Adiveta_1times mtimes g)

Итоговая формула:

(А;=;eta_1times mtimes qtimes(1;-;Т_2div Т_1))

Подставив значение, получаем ответ: 1,2*109 Дж.

Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.

Работы силы, формула

Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).

Работа силы — это скалярное произведение вектора силы на вектор перемещения.

Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:

Векторный вид записи

[ large boxed{ A = left( vec{F} , vec{S} right) }]

Для решения задач правую часть этой формулы удобно записывать в скалярном виде:

[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]

( F left( H right) ) – сила, перемещающая тело;

( S left( text{м} right) ) – перемещение тела под действием силы;

( alpha ) – угол между вектором силы и вектором перемещения тела;

Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.

В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.

Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.

Рассмотрим несколько случаев, следующих из формулы:

1. Когда угол между силой и перемещением острый, работа силы положительная;
2. А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
3. Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!

Работа — разность кинетической энергии

Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.

Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.

( E_{k1} left(text{Дж} right) )  – начальная кинетическая энергия машины;

( E_{k2} left(text{Дж} right) )  – конечная кинетическая энергия машины;

( m left( text{кг}right) ) – масса автомобиля;

( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.

Кинетическую энергию будем вычислять, используя формулу:

[ large E_{k} = m cdot frac{v^{2}}{2} ]

[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]

[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]

Теперь найдем разницу кинетической энергии в конце и вначале разгона.

[ large boxed{ A = Delta E_{k} }]

[ large Delta E_{k} = E_{k2} — E_{k1} ]

[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]

Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.

Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.

[ large boxed{ A = Delta E }]

Работа силы тяжести — разность потенциальной энергии

Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.

Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.

( E_{p1} left(text{Дж} right) )  – начальная потенциальная энергия яблока;

( E_{p2} left(text{Дж} right) )  – конечная потенциальная энергия яблока;

Примечание: Работу можно рассчитать через разность потенциальной энергии тела.

Потенциальную энергию будем вычислять, используя формулу:

[ large E_{p} = m cdot g cdot  h]

( m left( text{кг}right) ) – масса яблока;

Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.

( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.

Начальная высота яблока над поверхностью земли равна 3 метрам

[ large E_{p2} = 0,2 cdot 10 cdot  3 = 6 left(text{Дж} right) ]

Потенциальная энергия яблока на столе

[ large E_{p1} = 0,2 cdot 10 cdot  1 = 2 left(text{Дж} right) ]

Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.

[ large Delta E_{p} = E_{p2} — E_{p1} ]

[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]

Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!

Чтобы работа получилась положительной, в правой части формулы перед ( Delta  E_{p}) дополнительно допишем знак «минус».

[ large boxed{ A = — Delta E_{p} }]

Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.

Примечания:

1. Если тело падает на землю, работа силы тяжести положительна;
2. Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
3. Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
4. Работа силы тяжести не зависит от траектории, по которой двигалось тело;
5. Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.

Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.

Мощность

В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.

Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.

Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).

Расчет работы осуществляем, используя любую из формул:

[ large A = Delta E_{k} ]

[ large A = Delta E_{p} ]

[ large A = F cdot S cdot cos(alpha) ]

Разделив эту работу на время, в течение которого она совершалась, получим мощность.

[ large boxed{ P = frac{A}{Delta t} }]

Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.

Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.

Еще одна формула для расчета мощности

Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:

[ large P = left( vec{F} , vec{v} right) ]

Формулу можно записать в скалярном виде:

[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]

( F left( H right) ) – сила, перемещающая тело;

( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;

( alpha ) – угол между вектором силы и вектором скорости тела;

Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:

[ large boxed{ P = F cdot v }]

Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).

КПД

КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.

Примечания:

1. Процент – это дробь, у которой в знаменателе число 100.
2. КПД — это либо правильная дробь, или дробь, равная единице.

Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.

[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]

(eta) – КПД;

( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;

(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;

Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.

[ large boxed{ eta leq 1 }]

Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:

[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]

Выводы

1. Сила, приложенная к телу и перемещающая его, совершает работу;
2. Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
3. Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
4. Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
5. Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
6. Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
7. Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
8. Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
9. Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
10. КПД — это либо правильная дробь, или дробь, равная единице.
11. Можно вычислять КПД, подставляя в формулу работу, или мощности