График зависимости полезной мощности от сопротивления
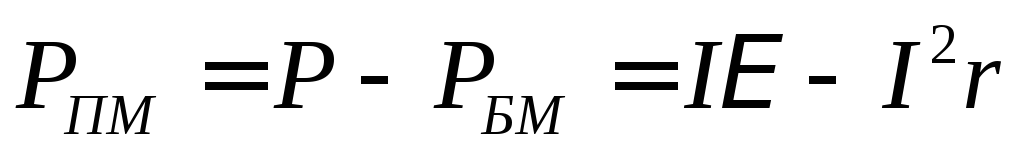
Пишу для школьников (для лучшего понимания ими основ физики). Материал излагаю в соответствии с признанной ныне научной трактовкой физических явлений. Критике существующей теории и глубоким теоретическим рассуждениям здесь не место.
На рисунке изображена замкнутая электрическая цепь, состоящая из источника постоянного тока и переменной нагрузки во внешней части цепи.
Источником постоянного тока может быть электрическая машина, о которой говорится в статье “Искровой разряд”; батарея гальванических элементов, аккумулятор и др.
Роль источника тока заключается в создании (генерировании) электрической энергии: в разделении положительных и отрицательных зарядов; в создании и поддерживании разности потенциалов между конечными точками цепи, в которую включена нагрузка (электрическая лампочка, электроплитка. электродвигатель и т. д.).
При прохождении тока через нагрузку электрическая энергия превращается в другие виды энергии :тепловую (в электроплитке); в тепло и свет (в электрической лампе); в механическую энергию (в электродвигателе).
Превращение энергии из одного вида в другой всегда связано с работой.
При прохождении тока по проводнику совершается работа, её совершают электрические силы (или электрическое поле). Кратко эту работу называют работой тока.
Рассматривая участок цепи, по которому проходит ток, получим следующее выражение для работы тока:
Работа тока равна произведению напряжения между концами участка на протекающий ток и время его протекания.
В случае, если участок цепи однородный (не содержит источника тока), то
тогда получим ещё две формулы для работы тока:
Если ток проходит через неподвижный проводник, то единственным результатом работы тока является его нагревание. Тогда количество выделившейся теплоты
Это запись закона Джоуля – Ленца.
Если кроме нагревания ток совершает ещё механическую работу, например, приводя в действие электродвигатель (мотор), то работа
лишь частично переходит в тепло.
В этом случае работа тока больше количества выделившейся теплоты, но закон Джоуля – Ленца выполняется.
Работа, совершаемая током в единицу времени, называется мощностью тока:
Единицей мощности тока является 1 Вт:
1 Вт – мощность выделяемая током 1 А в проводнике, между концами которого поддерживается напряжение 1 В.
Основная формула мощности для участка цепи:
Мощность постоянного тока на любом участке цепи выражается произведением силы тока на напряжение между концами участка цепи.
Так как для однородного участка цепи
то мощность можно найти ещё по формулам:
Обычно говорят не о работе, а о потребляемой из сети некоторым прибором (электроплитка, лампочки и др.) или двигателем (мотором) мощности электрического тока. Говоря о мощности (например, электродвигателя), отмечают, что работа двигателя совершается за счёт тока.
На приборах часто отмечается потребляемая ими мощность – мощность, необходимая для нормальной работы этого прибора.
Согласно закону сохранения энергии, для замкнутой электрической цепи можно записать:
Здесь
есть полная или затраченная работа, совершаемая сторонними силами, существующими внутри источника, по переносу заряда по цепи.
В гальваническом элементе такими силами являются силы химической реакции.
– это полезная работа, совершаемая электрическим полем при прохождении тока через нагрузку;
это работа, совершаемая внутри источника, по преодолению его внутреннего сопротивления.
Так как работа, совершённая за единицу времени, есть мощность, то из уравнения (1) получим выражение для мощности:
Здесь
есть полная или затраченная мощность, это мощность развиваемая источником тока.
это мощность выделяемая внутри источника тока
это полезная мощность, создаваемая во внешней части цепи (на нагрузке).
Здесь U – напряжение на зажимах источника при замкнутой цепи (при разомкнутой цепи оно равно ЭДС источника).
Так как для однородного участка цепи напряжение равно произведению тока на сопротивление, то полезную мощность можно найти ещё по следующей формуле:
Ток в замкнутой цепи
тогда формулу для полезной мощности можно записать так:
Проанализируем зависимость полезной мощности от сопротивления нагрузки.
При коротком замыкании вся развиваемая источником мощность выделяется на его внутреннем сопротивлении в виде теплоты.
Таким образом, полезная мощность, развиваемая во внешней цепи, достигает максимального значения тогда, когда сопротивление нагрузки равно внутреннему сопротивлению источника.
На следующем рисунке показан график зависимости полезной мощности от сопротивления нагрузки.
Получена формула для нахождения максимальной полезной мощности
При этом ток в цепи в два раза меньше тока короткого замыкания:
Но чему при этом будет равно КПД источника?
Коэффициент полезного действия (КПД) источника показывает, какая часть затраченной (полной) работы источника пошла на пользу или КПД есть отношение полезной работы к затраченной:
Получается, что если добиваться максимальной мощности во внешней цепи, то получим КПД работы всего 50%, то есть половина затраченной мощности источника расходуется бесполезно – переходит в тепло, нагревая источник тока.
Выгоднее брать сопротивление нагрузки больше внутреннего сопротивления источника. Тогда ток в цепи уменьшится, а КПД источника увеличится.
Подумайте над решением следующих задач.
1. ЭДС аккумулятора 2 В, его внутреннее сопротивление 0,4 Ом, сопротивление внешней цепи 1 Ом. Найти разность потенциалов на зажимах аккумулятора и КПД его работы. Ответ: 1,43 В; 71 %.
2. Какую максимальную полезную мощность может выделить аккумулятор с ЭДС 10 В и внутренним сопротивлением 1 Ом? Каково при этом сопротивление внешней цепи? Ответ: 25 Вт; 1 Ом.
3. КПД источника тока, замкнутого на внешнее сопротивление R, равно 60%. Каков будет КПД источника, если внешнее сопротивление увеличить в 6 раз? Ответ: 90%.
Ответ: 7,7 Вт; 12 Вт; 40%; 25%.
Ответ: 2,7 10 4 кг.
К.В. Рулёва
Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Сообщите друзьям о существовании этого канала.
Предыдущая запись: Решение задач на мощность тока.
Следующая запись: Ещё раз о зарядке и разрядке конденсатора.
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Источник
Для школьников.
При прохождении тока через нагрузку электрическая энергия превращается в другие виды энергии :тепловую (в электроплитке); в тепло и свет (в электрической лампе); в механическую энергию (в электродвигателе).
Превращение энергии из одного вида в другой всегда связано с работой.
Согласно закону сохранения энергии, для замкнутой электрической цепи можно записать:
Здесь
есть полная или затраченная работа, совершаемая сторонними силами, существующими внутри источника, по переносу заряда по цепи.
В гальваническом элементе сторонними силами являются силы химической реакции.
– это полезная работа, совершаемая электрическим полем при прохождении тока через нагрузку;
это работа, совершаемая внутри источника, по преодолению его внутреннего сопротивления.
Так как работа, совершённая за единицу времени, есть мощность, то из уравнения (1) получим выражение для мощности:
Здесь
есть полная или затраченная мощность, это мощность развиваемая источником тока.
это мощность выделяемая внутри источника тока
это полезная мощность, создаваемая во внешней части цепи (на нагрузке).
Здесь U – напряжение на зажимах источника при замкнутой цепи (при разомкнутой цепи оно равно ЭДС источника).
Так как для однородного участка цепи напряжение равно произведению тока на сопротивление, то полезную мощность можно найти ещё по следующей формуле:
Ток в замкнутой цепи
тогда формулу для полезной мощности можно записать так:
Проанализируем зависимость полезной мощности от сопротивления нагрузки.
При коротком замыкании вся развиваемая источником мощность выделяется на его внутреннем сопротивлении в виде теплоты.
Таким образом, полезная мощность, развиваемая во внешней цепи, достигает максимального значения тогда, когда сопротивление нагрузки равно внутреннему сопротивлению источника.
На следующем рисунке показан график зависимости полезной мощности от сопротивления нагрузки.
Получена формула для нахождения максимальной полезной мощности
При этом ток в цепи в два раза меньше тока короткого замыкания:
Но чему при этом будет равно КПД источника?
Из графика видно, что при равенстве сопротивления нагрузки и внутреннего сопротивления источника тока КПД источника равен 50%.
Коэффициент полезного действия (КПД) источника показывает, какая часть затраченной (полной) работы источника пошла на пользу или КПД есть отношение полезной работы к затраченной:
Задачи (теория дана в предыдущей записи)
1. ЭДС аккумулятора 2 В, его внутреннее сопротивление 0,4 Ом, сопротивление внешней цепи 1 Ом. Найти разность потенциалов на зажимах аккумулятора и КПД его работы.
Напряжение на зажимах аккумулятора:
Ток в цепи:
КПД аккумулятора:
Ответ: 1,43 В; 71 %.
2. Какую максимальную полезную мощность может выделить аккумулятор с ЭДС 10 В и внутренним сопротивлением 1 Ом? Каково при этом сопротивление внешней цепи?
Максимальная полезная мощность:
Полезная мощность достигает максимального значения при
Ответ: 25 Вт; 1 Ом.
3. КПД источника тока, замкнутого на внешнее сопротивление R, равно 60%. Каков будет КПД источника, если внешнее сопротивление увеличить в 6 раз?
Внутреннее сопротивление источника величина постоянная, его можно выразить из первого уравнения через R, затем найти второе значение КПД:
Ответ: 90%.
На приборах часто отмечается потребляемая ими мощность – мощность, необходимая для нормальной работы этого прибора.
Пишу для школьников. Материал излагаю в соответствии с признанной ныне научной трактовкой физических явлений. Критике существующей теории и глубоким теоретическим рассуждениям здесь не место.
К.В. Рулёва
Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Сообщите друзьям о существовании этого канала.
Предыдущая запись: Зарядка и разрядка конденсатора.
Следующая запись: Занятие 59. Электрический ток в электролитах.
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Источник
Рассмотрим
электрическую цепь, состоящую из
источника постоянного тока и внешнего
сопротивления R
(рис. 1). При протекании тока через
такую цепь источником ЭДС выполняется
работа и в цепи выделяется мощность.
Полезной
мощностью называют
мощность, которая выделяется на внешнем
сопротивлении. Из закона Джоуля-Ленца
(10*) полезная
мощность равняется
![]() ,
,
а из закона Ома для участка цепи![]() .
.
Тогда полезная мощность будет
| (1) |
где
![]() – падение напряжения на внешнем
– падение напряжения на внешнем
сопротивлении. При протекании тока по
цепи также выделяется „бесполезная”
мощность – разогревается источник ЭДС.
По закону Джоуля-Ленца эта мощность
равняется![]() .
.
Полная мощность, которая выделяется во
всей цепи, равняется![]() .
.
Используя закон Ома для полной цепи![]() ,
,
можно найти полную мощность
| (2) |
Итак,
полная мощность, которая выделяется в
цепи, равняется произведению силы тока
на ЭДС источника тока.
Пусть
в цепи можно менять внешнее сопротивление
![]() .
.
Проанализируем, как полезная и полная
мощности зависят от силы тока и внешнего
сопротивления.
Полезная
мощность
равняется разности между полной мощностью
и „бесполезной”:
| (3) |
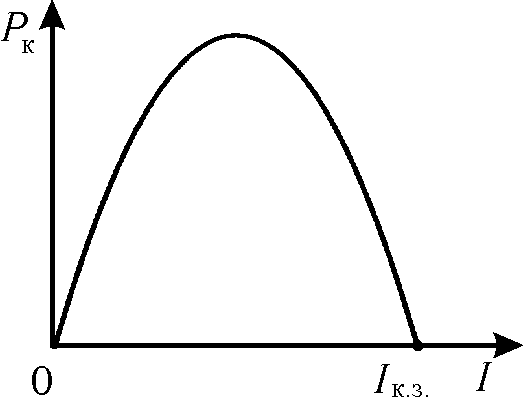
![]()
Рис. 2
Из этого
выражения видно, что полезная мощность
является квадратичной функцией силы
тока I.
График этой функции будет представлять
собой параболу (рис. 2).
Из рис. 2
вытекает, что
![]() в двух случаях:
в двух случаях:
когда
цепь разомкнута (R = ∞),
то сила тока в цепи I = 0;когда
возникло короткое заключение, при этом
R = 0,
а сила тока в цепи будет максимальной
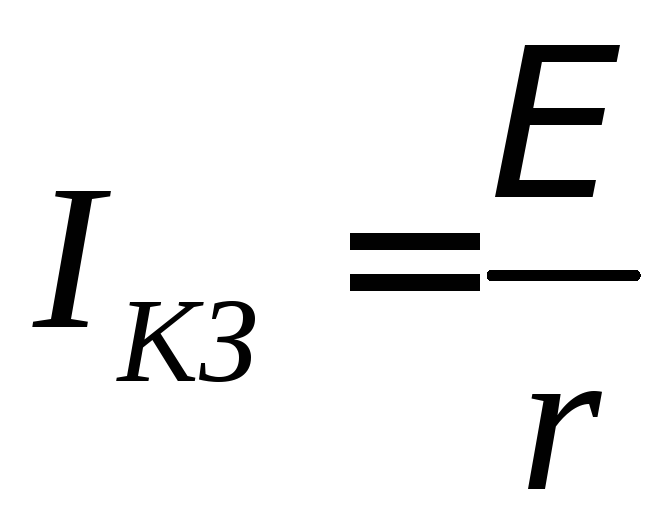 .
.
Меняя
величину внешнего сопротивления, можно
достичь некоторого значения силы тока
в цепи, при котором полезная мощность
будет максимальной. Найдем этот ток.
Для этого найдем первую производную
![]() и приравняем ее нулю. Из выражения (3)
и приравняем ее нулю. Из выражения (3)
имеем:
| (4) |
Отсюда
вытекает
| (5) |
а ток
![]() ,
,
при котором выделяется максимальная
полезная мощность, равняется![]() .
.
С другой стороны, на основании закона
Ома для полной цепи![]() ,
,
где![]() – сопротивление, при котором выделяется
– сопротивление, при котором выделяется
максимальная полезная мощность.
Приравнивая два последних выражения![]() ,
,
находим, что
| (6) |
Таким
образом, полезная
мощность будет максимальной при условии
равенства внешнего и внутреннего
сопротивлений.
Зависимость
полезной мощности от внешнего сопротивления
можно найти из закона
Джоуля-Ленца
![]() и закона Ома для полной цепи
и закона Ома для полной цепи![]()
| (7) |
График
зависимости
![]() показан на рис. 3 (криваяб).
показан на рис. 3 (криваяб).
Максимум функции
![]() можно найти, приравнивая
можно найти, приравнивая![]() нулю
нулю
| (8) |
Из
(8) также вытекает ожидаемое равенство
![]() .
.
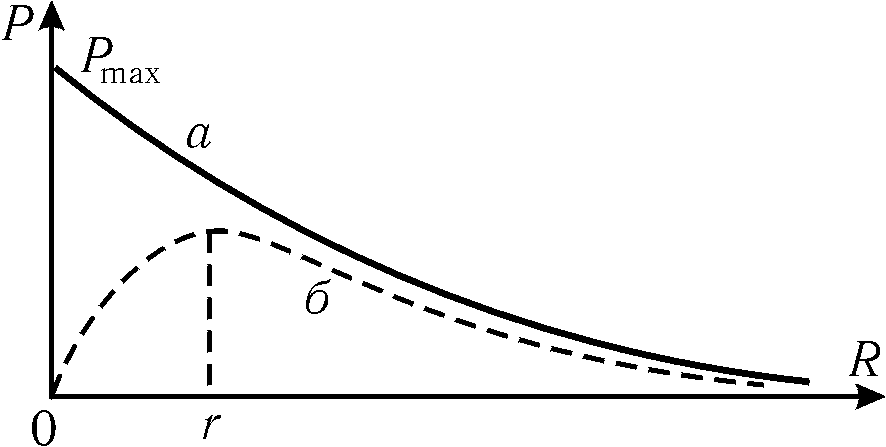
а
– полная мощность
б
– корисна потужність
Рис.
3
Рассмотрим
теперь, как полная мощность
зависит от внешнего сопротивления.
Используя выражение (2) и закон Ома для
полной цепи
![]() находим зависимость полной мощности
находим зависимость полной мощности
от внешнего сопротивления:
![]() .
.
(9)
График этой
зависимости показана на рис. 3 (кривая
а). При
изменении внешнего сопротивления от
нуля (короткое заключение) до бесконечности
(цепь разомкнута) полная мощность будет
убывать от максимального значения
![]() до нуля.
до нуля.
Зависимость
коэффициента полезного действия
источника электрического тока от силы
тока и внешнего сопротивления цепи
Коэффициент
полезного действия
(КПД) равняется отношению полезной
мощности (1) к полной мощности (2), которая
выделяется во всей цепи
| (10) |
Сначала
найдем зависимость КПД
от силы тока. Если
разделить выражение (3) для полезной
мощности на выражение (1) для полной
мощности, получим
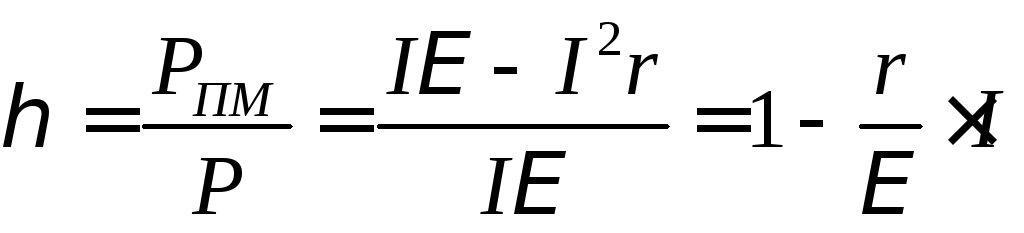
(11)
Итак,
КПД представляет собой линейную функцию
от силы тока (рис. 4). Когда I → 0
(цепь разомкнут), то
![]() .
.
При коротком заключении![]() ,
,
ток короткого заключения
| (12) |
и
КПД будет
![]() .
.
Чтобы найти
зависимость КПД от
внешнего сопротивления,
подставим в (9) выражение для
![]() из закона Ома для участки цепи
из закона Ома для участки цепи![]() ,
,
а выражение для![]() – из закона Ома для полной цепи
– из закона Ома для полной цепи![]() .
.
Тогда
| (13) |
Из соотношения (13)
вытекает:
при
R® 0
(короткое заключение,
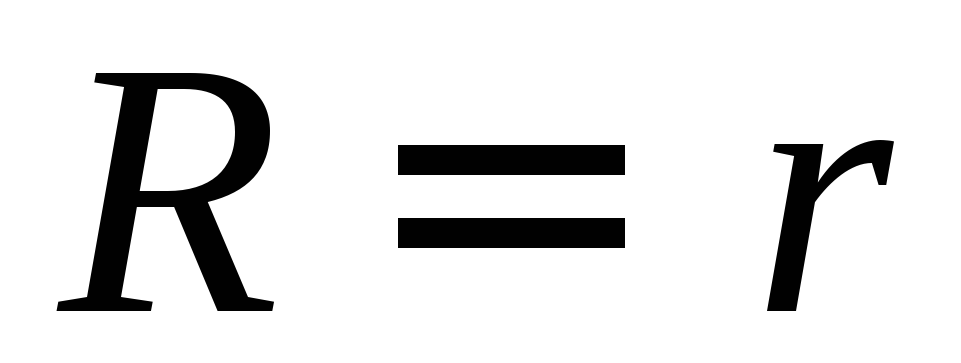 )
) ;
;при
R® ¥
( цепь разомкнут,
 )
) ;
;при
R = r
(условие максимума полезной мощности)
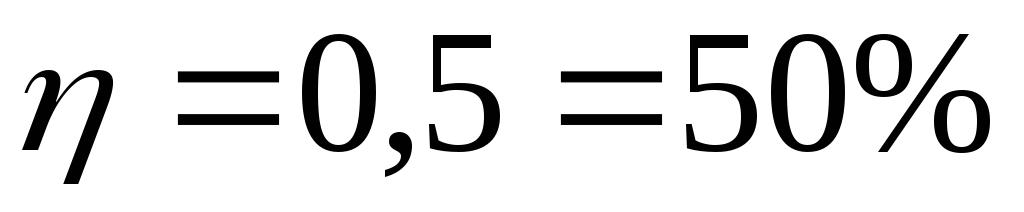 .
.
Приведенный
анализ показывает, что при увеличении
внешнего сопротивления КПД асимптотично
приближается к единице (рис. 5).
Соседние файлы в папке doc-формат
- #
- #
- #
- #
- #
- #
Источник
Определение и формула полезной мощности
Определение
Мощность – это физическая величина, которую использует как основную характеристику любого устройства, которое применяют
для совершения работы. Полезная мощность может быть использована для выполнения поставленной задачи.
Отношение работы ($Delta A$) к промежутку времени за которое она выполнена ($Delta t$) называют средней мощностью ($leftlangle Prightrangle $) за это время:
[leftlangle Prightrangle =frac{Delta A}{Delta t}left(1right).]
Мгновенной мощностью или чаще просто мощностью называют предел отношения (1) при $Delta tto 0$:
[P={mathop{lim }_{Delta tto 0} frac{Delta A}{Delta t} }=A'(t)left(2right).]
Приняв во внимание, что:
[Delta A=overline{F}cdot Delta overline{r }left(3right),]
где $Delta overline{r }$ – перемещение тела под действием силы $overline{F}$, в выражении (2) имеем:
[P={mathop{lim }_{Delta tto 0} left(frac{overline{F}cdot Delta overline{r }}{Delta t}right) }=overline{F}{mathop{lim }_{Delta tto 0} left(frac{Delta overline{r }}{Delta t}right)= }overline{F}cdot overline{v}left(4right),]
где $ overline{v}-$ мгновенная скорость.
Коэффициент полезного действия
При выполнении необходимой (полезной) работы, например, механической, приходится выполнять работу большую по величине, так как в реальности существуют силы сопротивления и часть энергии подвержена диссипации (рассеиванию). Эффективность совершения работы определяется при помощи коэффициента полезного действия ($eta $), при этом:
[eta =frac{P_p}{P}left(5right),]
где $P_p$ – полезная мощность; $P$ – затраченная мощность. Из выражения (5) следует, что полезная мощность может быть найдена как:
[P_p=eta P left(6right).]
Формула полезной мощности источника тока
Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:
[P=?I left(7right),]
где $?$ – ЭДС источника тока; $I$ – сила тока. При этом $P$ – полная мощность цепи.
Обозначим $U$ – напряжение на внешнем участке цепи, тогда формулу (7) представим в виде:
[P=?I=UI+I^2r=P_p+P_0left(8right),]
где $P_p=UI=I^2R=frac{U^2}{R}(9)$ – полезная мощность; $P_0=I^2r$ – мощность потерь. При этом КПД источника определяют как:
[eta =frac{P_p}{P_p+P_0}left(9right).]
Максимальную полезную мощность (мощность на нагрузке) электрический ток дает, если внешнее сопротивление цепи будет равно внутреннему сопротивлению источника тока. При этом условии полезная мощность равна 50% общей мощности.
При коротком замыкании (когда $Rto 0;;Uto 0$) или в режиме холостого хода $(Rto infty ;;Ito 0$) полезная мощность равна нулю.
Примеры задач с решением
Пример 1
Задание. Коэффициент полезного действия электрического двигателя равен $eta $ =42%. Какой будет его полезная мощность, если при напряжении $U=$110 В через двигатель идет ток силой $I=$10 А?
Решение. За основу решения задачи примем формулу:
[P_p=eta P left(1.1right).]
Полную мощность найдем, используя выражение:
[P=IUleft(1.2right).]
Подставляя правую часть выражения (1.2) в (1.1) находим, что:
[P_p=eta IU.]
Вычислим искомую мощность:
[P_p=eta IU=0,42cdot 110cdot 10=462 left(Втright).]
Ответ. $P_p=462$ Вт
Пример 2
Задание. Какова максимальная полезная мощность источника тока, если ток короткого замыкания его
равен $I_k$? При соединении с источником тока сопротивления $R$, по цепи (рис.1) идет ток силой $I$.
Решение. По закону Ома для цепи с источником тока мы имеем:
[I=frac{varepsilon}{R+r}left(2.1right),]
где $varepsilon$ – ЭДС источника тока; $r$ – его внутреннее сопротивление.
При коротком замыкании считаем, что сопротивление внешней нагрузки равно нулю ($R=0$), тогда сила тока короткого замыкания равна:
[I_k=frac{varepsilon}{r} left(2.2right).]
Максимальная полезная мощность в цепи рис.1 электрический ток даст, при условии:
[R=r left(2.3right).]
Тогда сила тока в цепи равна:
[I’=frac{varepsilon}{r+r}=frac{varepsilon}{2r}left(2.4right).]
Максимальную полезную мощность найдем, используя формулу:
[P_{p max}={I’}^2r={left(frac{varepsilon}{2r}right)}^2cdot r=frac{varepsilon^2}{4r}=frac{varepsilon^2}{4R}left(2.5right).]
Мы получили систему из трех уравнений с тремя неизвестными:
[left{ begin{array}{c}
I’=frac{varepsilon}{2r}, \
I_k=frac{varepsilon}{r}, \
P_{p max}={left(I’right)}^2r end{array}
left(2.6right).right.]
Используя первое и второе уравнения системы (2.6) найдем $I’$:
[frac{I’}{I_k}=frac{varepsilon}{2r}cdot frac{r}{varepsilon}=frac{1}{2}to I’=frac{1}{2}I_kleft(2.7right).]
Используем уравнения (2.1) и (2.2) выразим внутреннее сопротивление источника тока:
[varepsilon=Ileft(R+rright);; I_kr=varepsilon to Ileft(R+rright)=I_krto rleft(I_k+Iright)=IRto r=frac{IR}{I_k-I}left(2.8right).]
Подставим результаты из (2.7) и (2.8) в третью формулу системы (2.6), искомая мощность будет равна:
[P_{p max}={left(frac{1}{2}I_kright)}^2frac{IR}{I_k-I}.]
Ответ. $P_{p max}={left(frac{1}{2}I_kright)}^2frac{IR}{I_k-I}$
Читать дальше: формула равнодействующей всех сил.
Источник

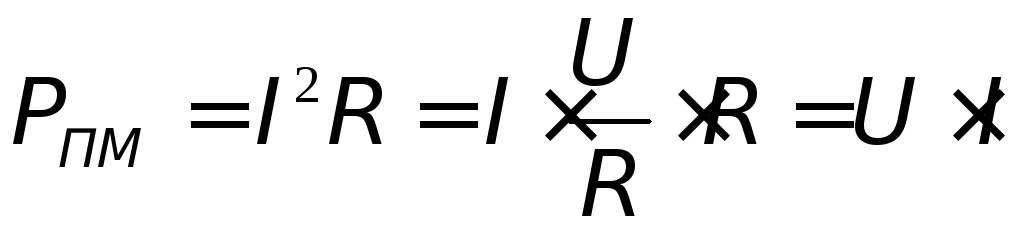 ,
,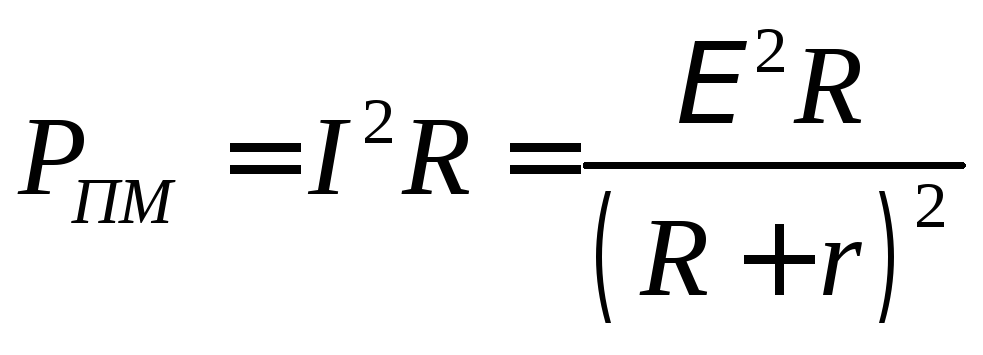 .
.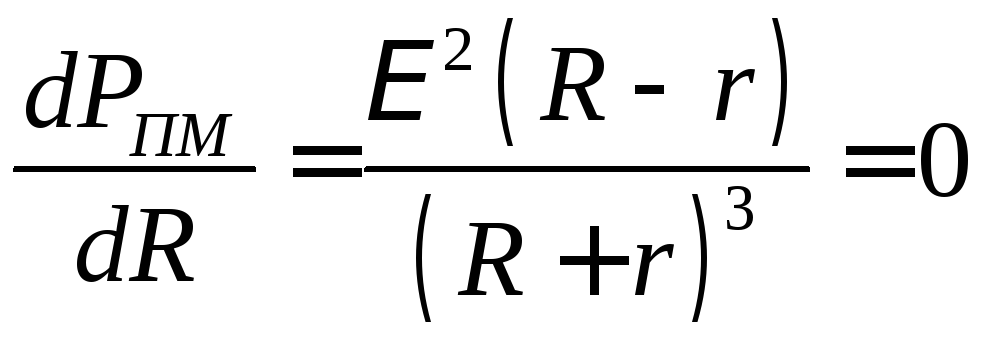 .
.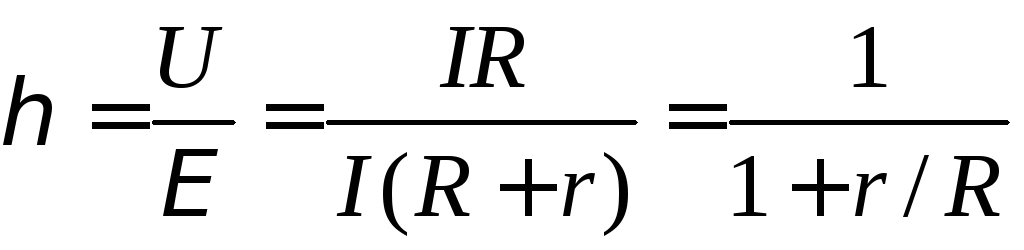 .
.