График зависимости полезной мощности от силы тока
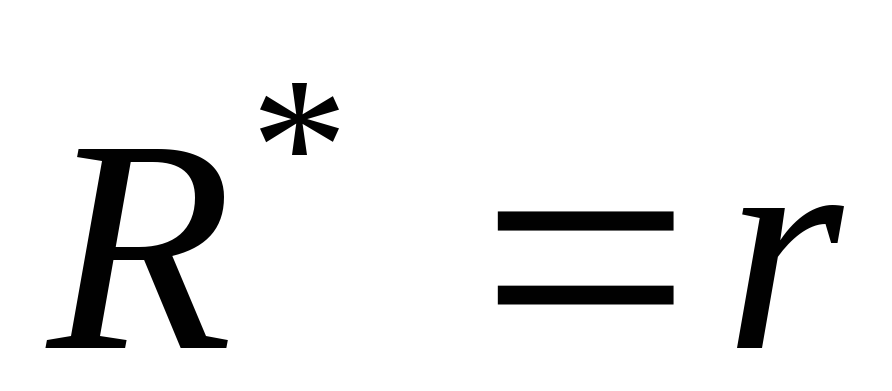
Пишу для школьников (для лучшего понимания ими основ физики). Материал излагаю в соответствии с признанной ныне научной трактовкой физических явлений. Критике существующей теории и глубоким теоретическим рассуждениям здесь не место.
На рисунке изображена замкнутая электрическая цепь, состоящая из источника постоянного тока и переменной нагрузки во внешней части цепи.
Источником постоянного тока может быть электрическая машина, о которой говорится в статье “Искровой разряд”; батарея гальванических элементов, аккумулятор и др.
Роль источника тока заключается в создании (генерировании) электрической энергии: в разделении положительных и отрицательных зарядов; в создании и поддерживании разности потенциалов между конечными точками цепи, в которую включена нагрузка (электрическая лампочка, электроплитка. электродвигатель и т. д.).
При прохождении тока через нагрузку электрическая энергия превращается в другие виды энергии :тепловую (в электроплитке); в тепло и свет (в электрической лампе); в механическую энергию (в электродвигателе).
Превращение энергии из одного вида в другой всегда связано с работой.
При прохождении тока по проводнику совершается работа, её совершают электрические силы (или электрическое поле). Кратко эту работу называют работой тока.
Рассматривая участок цепи, по которому проходит ток, получим следующее выражение для работы тока:
Работа тока равна произведению напряжения между концами участка на протекающий ток и время его протекания.
В случае, если участок цепи однородный (не содержит источника тока), то
тогда получим ещё две формулы для работы тока:
Если ток проходит через неподвижный проводник, то единственным результатом работы тока является его нагревание. Тогда количество выделившейся теплоты
Это запись закона Джоуля – Ленца.
Если кроме нагревания ток совершает ещё механическую работу, например, приводя в действие электродвигатель (мотор), то работа
лишь частично переходит в тепло.
В этом случае работа тока больше количества выделившейся теплоты, но закон Джоуля – Ленца выполняется.
Работа, совершаемая током в единицу времени, называется мощностью тока:
Единицей мощности тока является 1 Вт:
1 Вт – мощность выделяемая током 1 А в проводнике, между концами которого поддерживается напряжение 1 В.
Основная формула мощности для участка цепи:
Мощность постоянного тока на любом участке цепи выражается произведением силы тока на напряжение между концами участка цепи.
Так как для однородного участка цепи
то мощность можно найти ещё по формулам:
Обычно говорят не о работе, а о потребляемой из сети некоторым прибором (электроплитка, лампочки и др.) или двигателем (мотором) мощности электрического тока. Говоря о мощности (например, электродвигателя), отмечают, что работа двигателя совершается за счёт тока.
На приборах часто отмечается потребляемая ими мощность – мощность, необходимая для нормальной работы этого прибора.
Согласно закону сохранения энергии, для замкнутой электрической цепи можно записать:
Здесь
есть полная или затраченная работа, совершаемая сторонними силами, существующими внутри источника, по переносу заряда по цепи.
В гальваническом элементе такими силами являются силы химической реакции.
– это полезная работа, совершаемая электрическим полем при прохождении тока через нагрузку;
это работа, совершаемая внутри источника, по преодолению его внутреннего сопротивления.
Так как работа, совершённая за единицу времени, есть мощность, то из уравнения (1) получим выражение для мощности:
Здесь
есть полная или затраченная мощность, это мощность развиваемая источником тока.
это мощность выделяемая внутри источника тока
это полезная мощность, создаваемая во внешней части цепи (на нагрузке).
Здесь U – напряжение на зажимах источника при замкнутой цепи (при разомкнутой цепи оно равно ЭДС источника).
Так как для однородного участка цепи напряжение равно произведению тока на сопротивление, то полезную мощность можно найти ещё по следующей формуле:
Ток в замкнутой цепи
тогда формулу для полезной мощности можно записать так:
Проанализируем зависимость полезной мощности от сопротивления нагрузки.
При коротком замыкании вся развиваемая источником мощность выделяется на его внутреннем сопротивлении в виде теплоты.
Таким образом, полезная мощность, развиваемая во внешней цепи, достигает максимального значения тогда, когда сопротивление нагрузки равно внутреннему сопротивлению источника.
На следующем рисунке показан график зависимости полезной мощности от сопротивления нагрузки.
Получена формула для нахождения максимальной полезной мощности
При этом ток в цепи в два раза меньше тока короткого замыкания:
Но чему при этом будет равно КПД источника?
Коэффициент полезного действия (КПД) источника показывает, какая часть затраченной (полной) работы источника пошла на пользу или КПД есть отношение полезной работы к затраченной:
Получается, что если добиваться максимальной мощности во внешней цепи, то получим КПД работы всего 50%, то есть половина затраченной мощности источника расходуется бесполезно – переходит в тепло, нагревая источник тока.
Выгоднее брать сопротивление нагрузки больше внутреннего сопротивления источника. Тогда ток в цепи уменьшится, а КПД источника увеличится.
Подумайте над решением следующих задач.
1. ЭДС аккумулятора 2 В, его внутреннее сопротивление 0,4 Ом, сопротивление внешней цепи 1 Ом. Найти разность потенциалов на зажимах аккумулятора и КПД его работы. Ответ: 1,43 В; 71 %.
2. Какую максимальную полезную мощность может выделить аккумулятор с ЭДС 10 В и внутренним сопротивлением 1 Ом? Каково при этом сопротивление внешней цепи? Ответ: 25 Вт; 1 Ом.
3. КПД источника тока, замкнутого на внешнее сопротивление R, равно 60%. Каков будет КПД источника, если внешнее сопротивление увеличить в 6 раз? Ответ: 90%.
Ответ: 7,7 Вт; 12 Вт; 40%; 25%.
Ответ: 2,7 10 4 кг.
К.В. Рулёва
Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Сообщите друзьям о существовании этого канала.
Предыдущая запись: Решение задач на мощность тока.
Следующая запись: Ещё раз о зарядке и разрядке конденсатора.
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Источник
Рассмотрим
электрическую цепь, состоящую из
источника постоянного тока и внешнего
сопротивления R
(рис. 1). При протекании тока через
такую цепь источником ЭДС выполняется
работа и в цепи выделяется мощность.
Полезной
мощностью называют
мощность, которая выделяется на внешнем
сопротивлении. Из закона Джоуля-Ленца
(10*) полезная
мощность равняется
![]() ,
,
а из закона Ома для участка цепи![]() .
.
Тогда полезная мощность будет
| (1) |
где
![]() – падение напряжения на внешнем
– падение напряжения на внешнем
сопротивлении. При протекании тока по
цепи также выделяется „бесполезная”
мощность – разогревается источник ЭДС.
По закону Джоуля-Ленца эта мощность
равняется![]() .
.
Полная мощность, которая выделяется во
всей цепи, равняется![]() .
.
Используя закон Ома для полной цепи![]() ,
,
можно найти полную мощность
| (2) |
Итак,
полная мощность, которая выделяется в
цепи, равняется произведению силы тока
на ЭДС источника тока.
Пусть
в цепи можно менять внешнее сопротивление
![]() .
.
Проанализируем, как полезная и полная
мощности зависят от силы тока и внешнего
сопротивления.
Полезная
мощность
равняется разности между полной мощностью
и „бесполезной”:
| (3) |
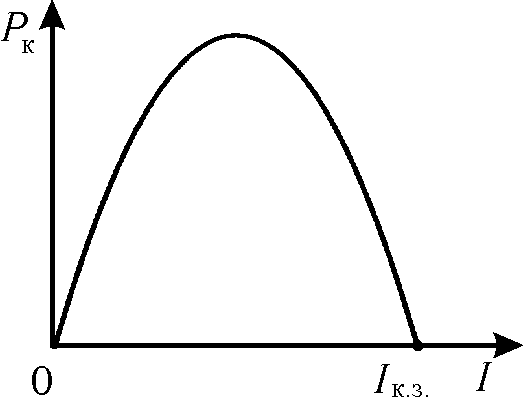
![]()
Рис. 2
Из этого
выражения видно, что полезная мощность
является квадратичной функцией силы
тока I.
График этой функции будет представлять
собой параболу (рис. 2).
Из рис. 2
вытекает, что
![]() в двух случаях:
в двух случаях:
когда
цепь разомкнута (R = ∞),
то сила тока в цепи I = 0;когда
возникло короткое заключение, при этом
R = 0,
а сила тока в цепи будет максимальной
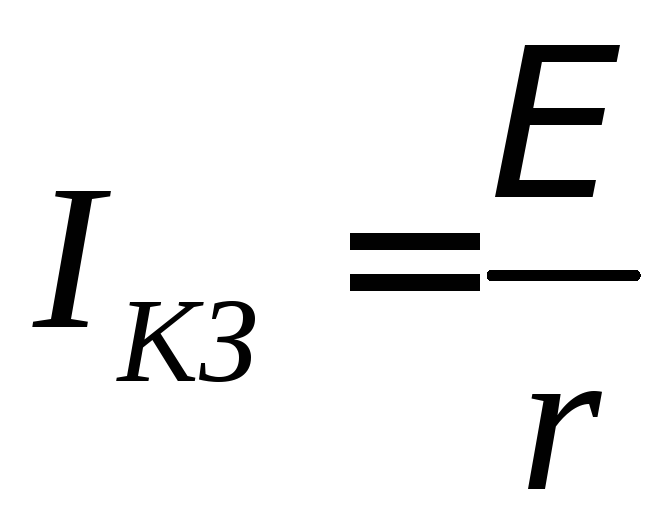 .
.
Меняя
величину внешнего сопротивления, можно
достичь некоторого значения силы тока
в цепи, при котором полезная мощность
будет максимальной. Найдем этот ток.
Для этого найдем первую производную
![]() и приравняем ее нулю. Из выражения (3)
и приравняем ее нулю. Из выражения (3)
имеем:
| (4) |
Отсюда
вытекает
| (5) |
а ток
![]() ,
,
при котором выделяется максимальная
полезная мощность, равняется![]() .
.
С другой стороны, на основании закона
Ома для полной цепи![]() ,
,
где![]() – сопротивление, при котором выделяется
– сопротивление, при котором выделяется
максимальная полезная мощность.
Приравнивая два последних выражения![]() ,
,
находим, что
| (6) |
Таким
образом, полезная
мощность будет максимальной при условии
равенства внешнего и внутреннего
сопротивлений.
Зависимость
полезной мощности от внешнего сопротивления
можно найти из закона
Джоуля-Ленца
![]() и закона Ома для полной цепи
и закона Ома для полной цепи![]()
| (7) |
График
зависимости
![]() показан на рис. 3 (криваяб).
показан на рис. 3 (криваяб).
Максимум функции
![]() можно найти, приравнивая
можно найти, приравнивая![]() нулю
нулю
| (8) |
Из
(8) также вытекает ожидаемое равенство
![]() .
.
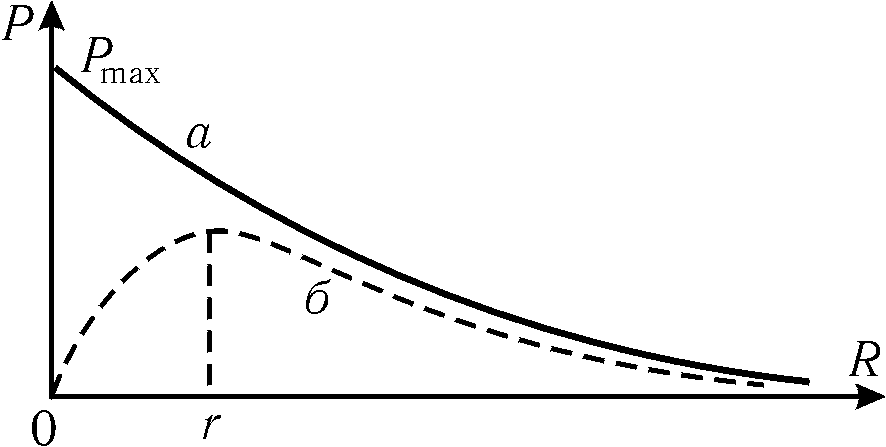
а
– полная мощность
б
– корисна потужність
Рис.
3
Рассмотрим
теперь, как полная мощность
зависит от внешнего сопротивления.
Используя выражение (2) и закон Ома для
полной цепи
![]() находим зависимость полной мощности
находим зависимость полной мощности
от внешнего сопротивления:
![]() .
.
(9)
График этой
зависимости показана на рис. 3 (кривая
а). При
изменении внешнего сопротивления от
нуля (короткое заключение) до бесконечности
(цепь разомкнута) полная мощность будет
убывать от максимального значения
![]() до нуля.
до нуля.
Зависимость
коэффициента полезного действия
источника электрического тока от силы
тока и внешнего сопротивления цепи
Коэффициент
полезного действия
(КПД) равняется отношению полезной
мощности (1) к полной мощности (2), которая
выделяется во всей цепи
| (10) |
Сначала
найдем зависимость КПД
от силы тока. Если
разделить выражение (3) для полезной
мощности на выражение (1) для полной
мощности, получим
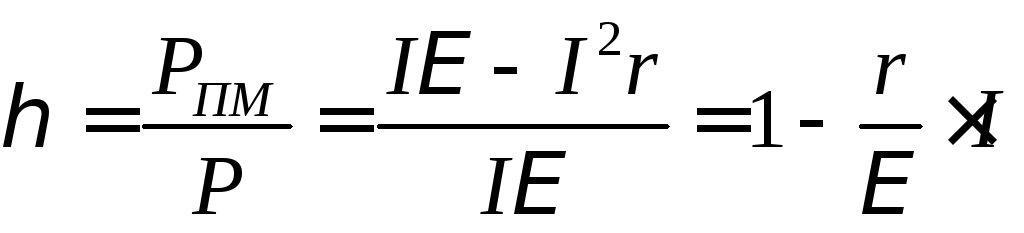
(11)
Итак,
КПД представляет собой линейную функцию
от силы тока (рис. 4). Когда I → 0
(цепь разомкнут), то
![]() .
.
При коротком заключении![]() ,
,
ток короткого заключения
| (12) |
и
КПД будет
![]() .
.
Чтобы найти
зависимость КПД от
внешнего сопротивления,
подставим в (9) выражение для
![]() из закона Ома для участки цепи
из закона Ома для участки цепи![]() ,
,
а выражение для![]() – из закона Ома для полной цепи
– из закона Ома для полной цепи![]() .
.
Тогда
| (13) |
Из соотношения (13)
вытекает:
при
R® 0
(короткое заключение,
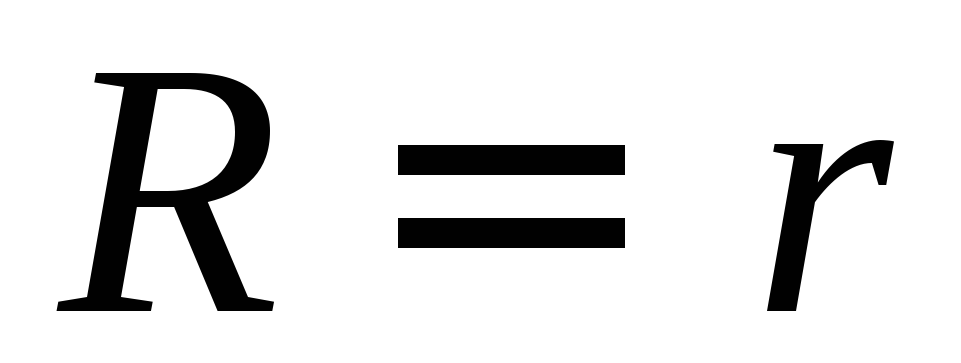 )
) ;
;при
R® ¥
( цепь разомкнут,
 )
) ;
;при
R = r
(условие максимума полезной мощности)
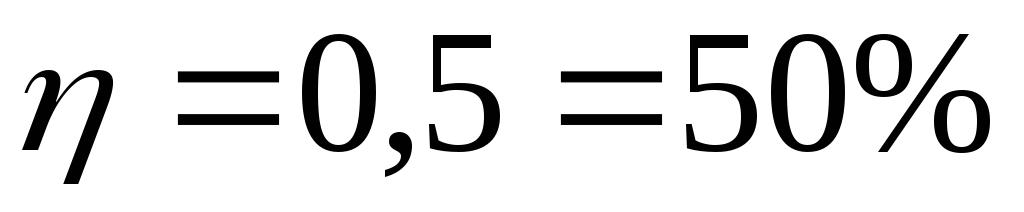 .
.
Приведенный
анализ показывает, что при увеличении
внешнего сопротивления КПД асимптотично
приближается к единице (рис. 5).
Соседние файлы в папке doc-формат
- #
- #
- #
- #
- #
- #
Источник
Для школьников.
При прохождении тока через нагрузку электрическая энергия превращается в другие виды энергии :тепловую (в электроплитке); в тепло и свет (в электрической лампе); в механическую энергию (в электродвигателе).
Превращение энергии из одного вида в другой всегда связано с работой.
Согласно закону сохранения энергии, для замкнутой электрической цепи можно записать:
Здесь
есть полная или затраченная работа, совершаемая сторонними силами, существующими внутри источника, по переносу заряда по цепи.
В гальваническом элементе сторонними силами являются силы химической реакции.
– это полезная работа, совершаемая электрическим полем при прохождении тока через нагрузку;
это работа, совершаемая внутри источника, по преодолению его внутреннего сопротивления.
Так как работа, совершённая за единицу времени, есть мощность, то из уравнения (1) получим выражение для мощности:
Здесь
есть полная или затраченная мощность, это мощность развиваемая источником тока.
это мощность выделяемая внутри источника тока
это полезная мощность, создаваемая во внешней части цепи (на нагрузке).
Здесь U – напряжение на зажимах источника при замкнутой цепи (при разомкнутой цепи оно равно ЭДС источника).
Так как для однородного участка цепи напряжение равно произведению тока на сопротивление, то полезную мощность можно найти ещё по следующей формуле:
Ток в замкнутой цепи
тогда формулу для полезной мощности можно записать так:
Проанализируем зависимость полезной мощности от сопротивления нагрузки.
При коротком замыкании вся развиваемая источником мощность выделяется на его внутреннем сопротивлении в виде теплоты.
Таким образом, полезная мощность, развиваемая во внешней цепи, достигает максимального значения тогда, когда сопротивление нагрузки равно внутреннему сопротивлению источника.
На следующем рисунке показан график зависимости полезной мощности от сопротивления нагрузки.
Получена формула для нахождения максимальной полезной мощности
При этом ток в цепи в два раза меньше тока короткого замыкания:
Но чему при этом будет равно КПД источника?
Из графика видно, что при равенстве сопротивления нагрузки и внутреннего сопротивления источника тока КПД источника равен 50%.
Коэффициент полезного действия (КПД) источника показывает, какая часть затраченной (полной) работы источника пошла на пользу или КПД есть отношение полезной работы к затраченной:
Задачи (теория дана в предыдущей записи)
1. ЭДС аккумулятора 2 В, его внутреннее сопротивление 0,4 Ом, сопротивление внешней цепи 1 Ом. Найти разность потенциалов на зажимах аккумулятора и КПД его работы.
Напряжение на зажимах аккумулятора:
Ток в цепи:
КПД аккумулятора:
Ответ: 1,43 В; 71 %.
2. Какую максимальную полезную мощность может выделить аккумулятор с ЭДС 10 В и внутренним сопротивлением 1 Ом? Каково при этом сопротивление внешней цепи?
Максимальная полезная мощность:
Полезная мощность достигает максимального значения при
Ответ: 25 Вт; 1 Ом.
3. КПД источника тока, замкнутого на внешнее сопротивление R, равно 60%. Каков будет КПД источника, если внешнее сопротивление увеличить в 6 раз?
Внутреннее сопротивление источника величина постоянная, его можно выразить из первого уравнения через R, затем найти второе значение КПД:
Ответ: 90%.
На приборах часто отмечается потребляемая ими мощность – мощность, необходимая для нормальной работы этого прибора.
Пишу для школьников. Материал излагаю в соответствии с признанной ныне научной трактовкой физических явлений. Критике существующей теории и глубоким теоретическим рассуждениям здесь не место.
К.В. Рулёва
Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Сообщите друзьям о существовании этого канала.
Предыдущая запись: Зарядка и разрядка конденсатора.
Следующая запись: Занятие 59. Электрический ток в электролитах.
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Источник
Мощность, развиваемая источником тока во всей цепи, называется полной мощностью.
Она определяется по формуле
где Pоб-полная мощность, развиваемая источником тока во всей цепи, вт;
Е- э. д. с. источника, в;
I-величина тока в цепи, а.
В общем виде электрическая цепь состоит из внешнего участка (нагрузки) с сопротивлением R и внутреннего участка с сопротивлением R0 (сопротивлением источника тока).
Заменяя в выражении полной мощности величину э. д. с. через напряжения на участках цепи, получим
Величина UI соответствует мощности, развиваемой на внешнем участке цепи (нагрузке), и называется полезной мощностью Pпол=UI.
Величина UoI соответствует мощности, бесполезно расходуемой внутри источника, Ее называют мощностью потерь Po=UoI.
Таким образом, полная мощность равна сумме полезной мощности и мощности потерь Pоб=Pпол+P0.
Отношение полезной мощности к полной мощности, развиваемой источником, называется коэффициентом полезного действия, сокращенно к. п. д.,и обозначается η.
Из определения следует
При любых условиях коэффициент полезного действия η ≤ 1.
Если выразить мощности через величину тока и сопротивления участков цепи, получим
Таким образом, к. п. д. зависит от соотношения между внутренним сопротивлением источника и сопротивлением потребителя.
Обычно электрический к. п. д. принято выражать в процентах.
Для практической электротехники особый интерес представляют два вопроса:
1. Условие получения наибольшей полезной мощности
2. Условие получения наибольшего к. п. д.
Наибольшую полезную мощность( мощность на нагрузке) электрический ток развивает в том случае, если сопротивление нагрузки равно сопротивлению источника тока.
Эта наибольшая мощность равна половине всей мощности (50%) развиваемой источником тока во всей цепи.
Половина мощности развивается на нагрузке и половина развивается на внутреннем сопротивлении источника тока.
Если будем уменьшать сопротивление нагрузки, то мощность развиваемая на нагрузке будет уменьшаться а мощность развиваемая на внутреннем сопротивлении источника тока будет увеличиваться.
Если сопротивление нагрузки равно нулю то ток в цепи будет максимальным, это режим короткого замыкания (КЗ). Почти вся мощность будет развивается на внутреннем сопротивлении источника тока. Этот режим опасен для источника тока а также для всей цепи.
Если сопротивление нагрузки будем увеличивать, то ток в цепи будет уменьшатся, мощность на нагрузке также будет уменьшатся. При очень большом сопротивлении нагрузки тока в цепи вообще не будет. Это сопротивление называется бесконечно большим. Если цепь разомкнута то ее сопротивление бесконечно большое. Такой режим называется режимом холостого хода.
Таким образом, в режимах, близких к короткому замыканию и к холостому ходу, полезная мощность мала в первом случае за счет малой величины напряжения, а во втором за счет малой величины тока.
Коэффициент полезного действия (к. п. д.) равен 100% при холостом ходе ( в этом случае полезная мощность не выделяется, но в то же время и не затрачивается мощность источника).
По мере увеличения тока нагрузки к. п. д. уменьшается по прямолинейному закону.
В режиме короткого замыкания к. п. д. равен нулю ( полезной мощности нет, а мощность развиваемая источником, полностью расходуется внутри него).
Подводя итоги вышеизложенному, можно сделать выводы.
Условие получения максимальной полезной мощности( R=R0) и условие получения максимального к. п. д. (R=∞) не совпадают. Более того, при получении от источника максимальной полезной мощности ( режим согласованной нагрузки) к. п. д.составляет 50%, т.е. половина развиваемой источником мощности бесполезно затрачивается внутри него.
В мощных электрических установках режим согласованной нагрузки является неприемлемым, так как при этом происходит бесполезная затрата больших мощностей. Поэтому для электрических станций и подстанций режимы работы генераторов, трансформаторов, выпрямителей рассчитываются так, чтобы обеспечивался высокий к. п. д. ( 90% и более).
Иначе обстоит дело в технике слабых токов. Возьмем, например, телефонный аппарат. При разговоре перед микрофоном в схеме аппарата создается электрический сигнал мощностью около 2 мвт. Очевидно, что для получения наибольшей дальности связи необходимо передать в линию как можно большую мощность, а для этого требуется выполнить режим согласованного включения нагрузки. Имеет ли в данном случае существенное значение к. п. д.? Конечно нет, так как потери энергии исчисляются долями или единицами милливатт.
Режим согласованной нагрузки применяется в радиоаппаратуре. В том случае, когда согласованный режим при непосредственном соединении генератора и нагрузки не обеспечивается, применяют меры согласования их сопротивлений.
Источник

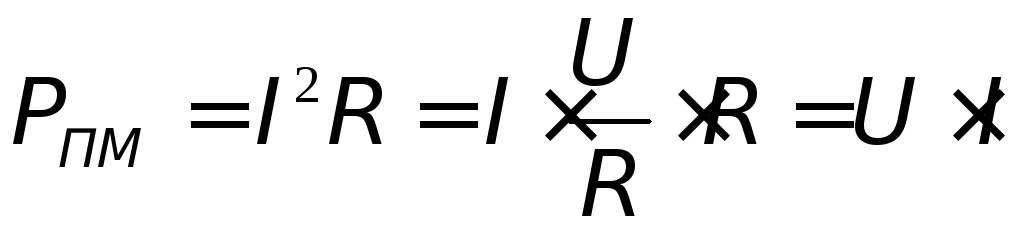 ,
,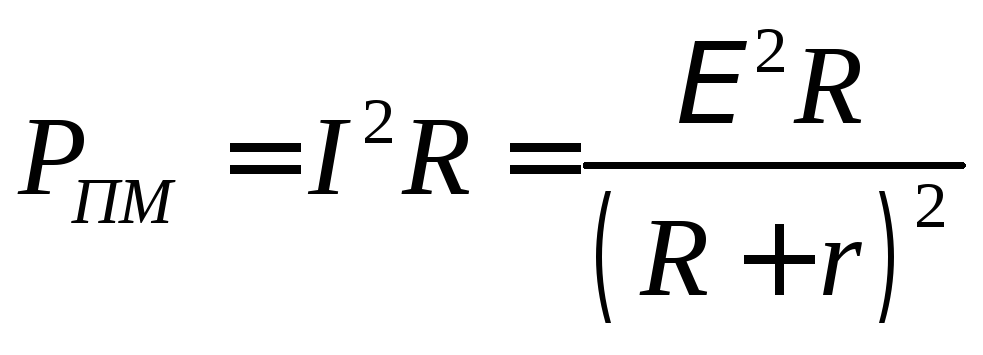 .
.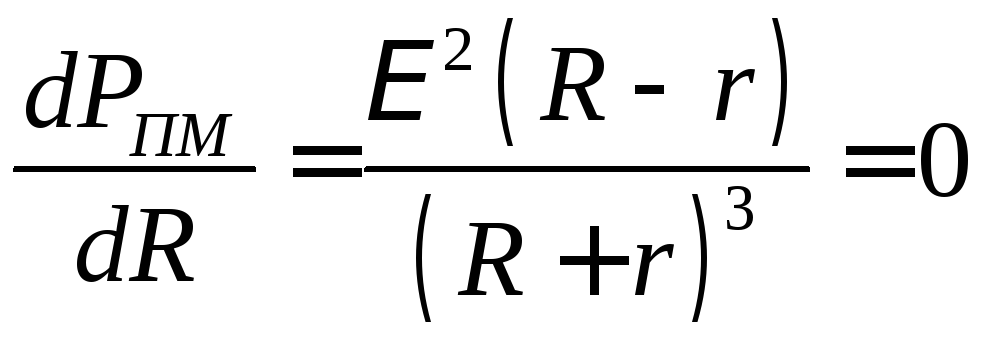 .
.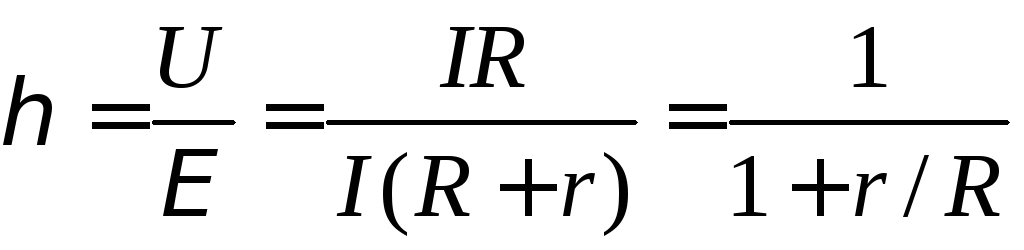 .
.