Фигуры из кусочков квадрата к числу полезных
Функция
[x]
равна наибольшему целому числу,
превосходящемуx
(x
– любое действительное число). Например:
Функция
[x]
имеет «точки разрыва»: при целых
значениях x
она «изменяется скачком».
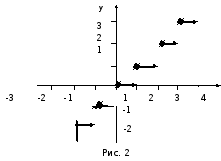
На
рис.2 дан график этой функции, причем
левый конец каждого из горизонтальных
отрезков принадлежит графику (жирные
точки), а правый – не принадлежит.
Попробуйте
доказать,
что если каноническое разложение числа
n!
есть
,
то
Аналогичные
формулы имеют место для
Зная
это, легко определить, например, сколькими
нулями оканчивается число 100! Действительно,
пусть
.
Тогда
и
.
Следовательно,
100! Делится на
,
т.е. оканчивается двадцатью четырьмя
нулями.
Фигуры из кусочков квадрата
К
числу полезных и увлекательных
развлечений относится составление
фигур из семи кусочков квадрата,
разрезанного в соответствии с рис.3,
(а), причем при составлении заданных
фигур должны быть использованы все
семь кусочков, и они должны налегать,
даже частично, друг на друга.
На
рис. 4 приведены симметричные фигуры1.
Попробуйте сложить эти фигуры из частей
квадрата, изображенного на рис. 3, (а).
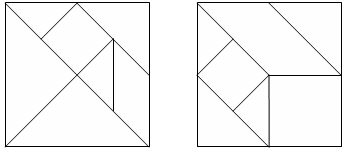
(а) (b)
Рис.3
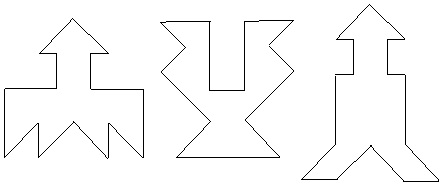
Рис.
4
Из
этих же чертежей можно складывать и
многие другие фигуры (например,
изображения различных предметов,
животных и т.п.).
Менее
распространенным вариантом игры
является составление фигур из кусочков
квадрата, изображенного на рис. 3, (b).
Магические квадраты
Магические
квадрат «n2-квадратом»
назовем
квадрат, разделенный на n2
клеток,
заполненных первыми n2
натуральными
числами так, что суммы чисел, стоящих
в любом горизонтальном или вертикальном
ряду, а также на любой из диагоналей
квадрата, равны одному и тому же числу
Если
одинаковы лишь суммы чисел, стоящих в
любом горизонтальном и вертикальном
ряду, то квадрат называется полумагическим.
16 | 3 | 2 | 13 |
5 | 10 | 11 | 8 |
9 | 6 | 7 | 12 |
4 | 15 | 14 | 1 |
Магический
42
–квадрат назван именем Дюрера, математика
и художника XVIвека,
изображавшего квадрат на известной
картине «Меланхолия».
Кстати,
два нижних средних числа этого квадрата
образуют число 1514-дату создания картины.
Существует
лишь восемь девятиклеточных
магических квадратов.
Два
из них, являющиеся зеркальным изображением
друг друга, приведены на рисунке;
остальные шесть могут быть получены
из этих квадратов вращение их вокруг
центра на 90°, 180°, 270°
2.
Нетрудно полностью исследовать вопрос
о магических квадратов при n=3
Действительно,S3
= 15 , и существует лишь восемь способов
представления числа 15 в виде суммы
различных чисел (от единицы до девяти):
15=1+5+9=1+6+8=2+4+9=2+5+8=2+6+7=3+4+8=3+5+7=4+5+6
Заметим,
что каждое из чисел 1, 3, 7, 9 входит в две,
а каждое из чисел 2, 4, 6, 8 – в три указанные
суммы и лишь число 5 входит в четыре
суммы. С другой стороны, из восьми
трехклеточных рядов: трех горизонтальных,
трех вертикальных и двух диагональных
– через каждую из угловых клеток
квадрата проходит по три, через
центральную клетку по четыре и через
каждую из остальных клеток по два ряда.
Следовательно, число 5 должно обязательно
стоять в центральной клетке, числа 2,
4, 6, 8 – в угловых клетках, а числа 1, 3, 7,
9 – в остальных клетках квадрата.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
К числу полезных и увлекательных развлечений относится составление фигур из семи кусочков квадрата, разрезанного в соответствии с рис.3, (а), причем при составлении заданных фигур должны быть использованы все семь кусочков, и они должны налегать, даже частично, друг на друга.
На рис. 4 приведены симметричные фигуры[1]. Попробуйте сложить эти фигуры из частей квадрата, изображенного на рис. 3, (а).
(а) (b)
Рис.3
Рис. 4
Из этих же чертежей можно складывать и многие другие фигуры (например, изображения различных предметов, животных и т.п.).
Менее распространенным вариантом игры является составление фигур из кусочков квадрата, изображенного на рис. 3, (b).
Магические квадраты
Магические квадрат «n2-квадратом» назовем квадрат, разделенный на n2 клеток, заполненных первыми n2 натуральными числами так, что суммы чисел, стоящих в любом горизонтальном или вертикальном ряду, а также на любой из диагоналей квадрата, равны одному и тому же числу
Если одинаковы лишь суммы чисел, стоящих в любом горизонтальном и вертикальном ряду, то квадрат называется полумагическим.
Магический 42 –квадрат назван именем Дюрера, математика и художника XVIвека, изображавшего квадрат на известной картине «Меланхолия».
Кстати, два нижних средних числа этого квадрата образуют число 1514-дату создания картины.
Существует лишь восемь девятиклеточных магических квадратов. Два из них, являющиеся зеркальным изображением друг друга, приведены на рисунке; остальные шесть могут быть получены из этих квадратов вращение их вокруг центра на 90°, 180°, 270°
2. Нетрудно полностью исследовать вопрос о магических квадратов при n=3
Действительно,S3 = 15 , и существует лишь восемь способов представления числа 15 в виде суммы различных чисел (от единицы до девяти):
15=1+5+9=1+6+8=2+4+9=2+5+8=2+6+7=3+4+8=3+5+7=4+5+6
Заметим, что каждое из чисел 1, 3, 7, 9 входит в две, а каждое из чисел 2, 4, 6, 8 – в три указанные суммы и лишь число 5 входит в четыре суммы. С другой стороны, из восьми трехклеточных рядов: трех горизонтальных, трех вертикальных и двух диагональных – через каждую из угловых клеток квадрата проходит по три, через центральную клетку по четыре и через каждую из остальных клеток по два ряда. Следовательно, число 5 должно обязательно стоять в центральной клетке, числа 2, 4, 6, 8 – в угловых клетках, а числа 1, 3, 7, 9 – в остальных клетках квадрата.
Приложение
1. Как известно, .
Если перебирать по порядку эти множители, то через каждые «шагов»
будут встречаться множители, кратные простому числу ; число их
равно , но из них множителей делятся на , – делятся на и
т.д.
Следовательно, число множителей в равенстве в состав которых множитель входит ровно один, два, три и т.д. раза, соответственно равно числам:
Поэтому
2. Нетрудно полностью исследовать вопрос о магических квадратах при n=3. Действительно, S3=15, и существует лишь восемь способов представления числа 15 в виде суммы различных чисел (от единицы до девяти):
15=1+5+9=1+6+8=2+4+9=2+5+8=2+6+7=3+4+8=3+5+7=4+5+6.
Заметим, что каждое из чисел 1, 3, 7, 9 входит в две, а каждое из чисел 2, 4, 6, 8- в три указанные суммы и лишь число 5 входит в четыре суммы. С другой стороны, из восьми трехклеточных рядов: трех горизонтальных, трех вертикальных и двух диагональных – через каждую из угловых клеток квадрата проходит по три, через центральную клетку по четыре и через каждую из остальных клеток по два ряда. Следовательно, число 5 должно обязательно стоять в центральной клетке, числа 2, 4, 6, 8 – в угловых клетках, а числа 1, 3, 7,9 – в остальных клетках квадрата.
Удивительные встречи с занимательной математикой
Интереснейший набор задач
Прекрасное лицо царицы наук МАТЕМАТИКИ
[1]Фигуры заимствованы из книги В.И. Обреимова «Тройная головоломка»
Методики Никитина – это и интеллектуальные развивающие игры различных уровней сложности, некоторые из них будут интересны даже взрослым! Игры в основном представлены в виде головоломок на распознавание и достраивание образов, при которых делается упор на развитие логического и образного мышления.
Игра квадраты Никитина состоит из трех уровней и первый самый простой. Представлены в двух пополнениях МАКСИ и МИНИ.
Самыми известными из пособий Никитиных являются оригинальный развивающий комплект Сложи квадрат. Раньше его можно было сделать только своими руками, а теперь Квадрат Никитиных выпускается игровой промышленностью в больших количествах и во всех возможных вариантах.
Игра сложить квадрат Никитина 1 уровень (мини)
В нем есть две рамочки-планшета, в которые вставляются детали шести квадратов. На этом этапе они состоят из двух или трех частей. Малыши уже с полутора лет могут собирать такие простые головоломки и одновременно изучать цвета.
Перед тем как предложить малышу игру «Сложи квадрат» Никитина нужно предложить ему разделить все детальки по цветам, ведь кубик состоит только из одноцветных составляющих.
1 уровень сложности – для детей 2-4 года.
В набор входит: 2 планшета с выемками для квадратов и 12 разрезных квадратов (6*6см)
Игра сложить квадрат Никитина 2 уровень (мини)
В этом комплекте, всё так же, состоящем из двух планшетов, разделенных на шесть квадратов, уже более сложное задание. Квадратики тут разделены уже на 4, 5 и 6 сегментов, что намного усложняет работу малышу и позволяет активизировать его умственные способности, развивая их.
Логическое и аналитическое мышление активно участвует в процессе игры, ведь недаром эти игры называются дидактическими – то есть развивающими. Если ребенку захотелось выйти за рамки простых квадратов, не мешайте ему, ведь пространственное мышление – это замечательно. Малыш может строить различные фигурки, которые придут ему на ум при помощи цветных кусочков.
2 уровень сложности – для детей 4-5 года.
В набор входит: 2 планшета с выемками для квадратов и 12 разрезных квадратов (6*6см)
Игра сложить квадрат Никитина 3 уровень (мини)
Самый сложный уровень подразумевает деление квадратов на крупные и мелкие части – от 4 до 7. Это довольно непростая работа даже для взрослого и от ребенка она требует большой концентрации внимания и работы как зрительных, так и умственных анализаторов.
3 уровень сложности – для детей 6-7 лет. Так же подходят и взрослым!
В набор входит: 2 планшета с выемками для квадратов и 12 разрезных квадратов (6*6см)
Есть также вариант МАКСИ – все квадраты 2 уровня на одном планшете.
“Сложи квадрат” Б.П.Никитин, 1 уровень (макси)
“Сложи квадрат” Б.П.Никитин, 2 уровень (макси)
“Сложи квадрат” Б.П.Никитин, 3 уровень (макси)
Описание игры
Эта игра возникла из головоломки, в которой требовалось из нескольких кусочков различной формы сложить квадрат. Головоломка была трудна даже для взрослых, но за нее брались и дети, и безуспешность их попыток натолкнула нас на мысль сделать ряд более простых заданий, которые постепенно подведут к решению сложного.
Как можно играть?
1. Берем первую рамочку и высыпаем из нее квадраты! Это кстати, тоже очень весело! Просим ребенка, перевернуть все кусочки цветной стороной вверх и просто сложить их по цвету в кучки. Здесь можно познакомить малыша с понятием холодные и теплые оттенки, естественно, приводя соответствующие примеры:
• желтое солнышко, красный огонь, оранжевые апельсины – теплые;
• голубое холодное море, синее дождливое небо — холодные;
• зеленый может быть и теплым и холодным, ведь он состоит из теплого желтого и холодного синего и все зависит от того, какого цвета в нем больше).
Здесь же вы знакомите малыша с последовательностью цветов в радуге и можно давать задания собрать квадраты в порядке «Каждый охотник желает знать, где сидит фазан». В квадратах отсутствует фиолетовый цвет.
2. Собираем квадраты в рамках. Все задания должны быть под силу малышу. Если затрудняется и не хочет, лучше не заставлять. Можно просто показать, что все кусочки переворачиваются и просто нужно пробовать разные варианты.
3. Собираем квадраты без рамок – на столе, на полу. Обязательно обыгрываем этот процесс – мы строим многоэтажный дом или поезд с вагончиками и т.д.
4. Собираем квадраты из разноцветных деталей. То есть не одного цвета, а комбинируем из разных деталей.
5. Строим из кусочков различные фигуры.
Если малыш еще не в состоянии сделать это сам, предлагаем родителям проявить творчество и придумать рисунки из отдельных кусочков (для упрощения можно обвести кусочки соответствующим цветом). Ребенку нужно просто найти каждую деталь и наложить на ваш пример.
Если малыш уже достаточно взрослый, ему будет понятно задание по одному вашему примеру.
Вот варианты фигур и рисунков ребенка в возрасте 3,5 года.
6. Вместе с квадратами можно знакомить малыша не только с цветами, но и с образом цифры. А именно – каждую деталь отдельного квадрата подписываем цифрой. Все детали красного квадрата первой рамки первого уровня – цифра 1, все детали оранжевого квадрата первой рамки первого уровня цифра 2 и т.д.
Если учесть, что у нас по 12 квадратов в каждом уровне, то 12*3=36. Значит ребенок будет знать числа до 36.
Задания: сортировать кусочки по числам; собирать квадраты тыльной стороной (не используя цвет, а числа).
Добавляем в Квадраты Никитина другие игрушки.
Учимся обводить предметы по контуру, усложняя задание – обвести несколько фигур так, чтобы получился рисунок (домик, кораблик). То есть это задание противоположно 5-му заданию. Ребенок не просто придумывает рисунок из деталей, но еще и зарисовывает картины.
8. Берем 3 предмета (большой, средний и маленький) и просим поставить их на квадрат определенного цвета. По мере возможностей ребенка усложняем задание: поставь среднюю фигуру на квадрат между зеленым и синим квадратом, маленький предмет поставить над большим.
Таким образом комбинируем понятия цвета, размера, расположения в пространстве (слева, справа, сверху, внизу, над, под, между).
9. Усложняем третье задание – строим поезд или дом и заселяем его пассажирами или жителями. И снова комбинируем разнообразные задания, расширяя знакомство с цветами, расположением (впереди, сзади, между, слева, справа).
Можно присоединить еще и знакомство с фигурами (поставь круг в вагончик между зеленым и синим вагончиками и т.п.)
Не забываем о цифрах и в более позднем возрасте порядковый счет (первый вагончик, второй, третий, … десятый). На фото поезд едет вправо, а нумерация вагонов с головы:)
10. Если есть в наличии карточки, например с животными и их детенышами, можно использовать рамки из-под квадратов как домики. Малыш поселяет в домики детенышей, а когда мамы возвращаются домой с охоты, помогает им найти своих деток.
11. Квадраты можно использовать логопедам при автоматизации звуков. Например, подбираете 7 картинок со звуком «Ш», причем 6 из них – одежда, 1 – обувь. Ребенок, называя правильно каждую картинку, вкладывает в рамку. Определяется с тем, какая картинка лишняя (в нашем случае — обувь) и накрывает 6 правильных квадратами. После пытается вспомнить, где какая картинка спрятана (тренировка визуальной памяти). Если же малыш не помнит, открываете не весь квадрат, а только одну деталь и ребенок по фрагменту вспоминает (формирование целого по фрагменту), что же там спрятано.
Функция[х]
равна
наибольшему целому числу, не превосходящему
х (х
–
любое действительное число). Например:
2,=
– 4 ,=
6.
Функция
[х]
имеет
«точки разрыва»: при целых значениях х
она «изменяется скачком».
На
рис. 2 дан график этой функции, причем
левый конец каждого из горизонтальных
отрезков принадлежит графику (жирные
точки),а правый — не принадлежит.
Попробуйте
доказать, что если каноническое
разложение числаn!
есть
n!=
p1α
•
p2β•p3γ•…
•pkδ,
то
α =
+ …
Аналогичные
формулы имеют месть для β,
γ, …, δ.
Зная
то, легко определить, например, сколькими
нулями оканчивается число 100! Действительно,
пусть 100!=.
Тогда
и
.
Следовательно,
100! делится на
,
т.е оканчивается двадцатью четырьмя
нулями.
Фигуры из кусочков квадрата
К
числу полезных и увлекательных развлечений
относится составление фигур из семи
кусочков квадрата, разрезанного в
соответствии с рис.3, (а), причем при
составлении заданных фигур должны быть
использованы все семь кусочков, и
они не должны налегать друг на друга.
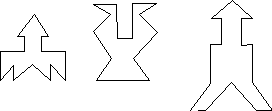
На
рис. 4 приведены симметричные фигуры.
Попробуйте сложить эти фигуры1из частей квадрата, изображенного на
рис.3, (а)
Из
этих же чертежей можно складывать и
многие другие фигуры (например, изображение
различных методов, животных и т.п.).
Менее
распространенным вариантом игры является
составление фигур из кусочков квадрата,
изображенного на рис. 3, (b).
Магические квадраты
Магическим
«n2-квадратом»
назовем квадрат, разделенный на n2
клеток,
заполненных
первыми n2
натуральными
числами так, что суммы чисел,стоящих в
любом горизонтально или вертикальном
ряду, а также на любой из диагоналей
квадрата, равны одному и тому же числу
.
Если
одинаковы лишь суммы чисел, стоящих в
любом горизонтальном или вертикальном
ряду, то квадрат называется полумагическим.
16 | 3 | 2 | 13 |
5 | 10 | 11 | 8 |
9 | 6 | 7 | 12 |
4 | 15 | 14 | 1 |
Магический
42-квадрат имеет название Дюрера,
математика и художникаXVI
века, изобразившего квадрат на
известной картине «Меланхолия». Кстати,
два нижних средних числа этого квадрата
образуют число 1514-дату создания картины.
Существует
лишь восемь девятиклеточных магических
квадратов.Два из них, являющиеся
зеркальным изображением друг друга,
приведены на рисунке; остальные шесть
могут быть получены из этих квадратом
вращением их вокруг центра на 90о,
180о, 270о.
Приложение №1
Как
известно, n!=(**)Если
перебирать по порядку эти множители,
то через каждые р1 «шагов» будут
встречаться множители, кратные простому
числу р1; число их равно,
но из нихмножителей
делятся на р12,-
делятся на р13 и т.д.Следовательно,
число множителей в равенстве (**), в
состав которых множитель р1входит
ровно один, два, три и т.д. Раза ,
соответственно равно числам:и
т.д.
Поэтому
α==
=+++…
Соседние файлы в папке ИНФОРМАТИКА
- #
- #
- #
12.02.2015499.29 Кб49math_games..odt
- #
- #
12.02.201593.98 Кб13Вычисления и диаграммы.ods
- #
12.02.2015190 б9Документ TeX 1.aux
- #
12.02.20151.46 Кб9Документ TeX 1.dvi
- #
Ф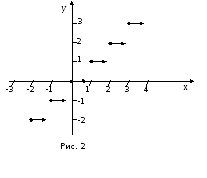
ункция
[х]
равна наибольшему целому числу, не
превосходящему х
(х
–любое действительное число). Например:
,
,
[6]=6.
Функция
[x]
имеет «точки разрыва»: при целых
значениях х она «изменяется скачком».
На
рис.2 дан график этой функции, причём
левый конец каждого из горизонтальных
отрезков принадлежит графику (жирные
точки), а правый – не принадлежит.
Попробуйте
доказать,
что если каноническое разложение числаn!
есть
=
, то α =
Аналогичные
формулы имеют место для β,γ,…,δ.
Зная
это, легко определить, например, сколькими
нулями оканчивается число 100! Действительно,
пусть 100!
=
·
·
·…·97δ.
Тогда
и
γ=
Следовательно,
100! делится на (2·5)24,
т.е. оканчивается двадцатью четырьмя
нулями.
Фигуры из кусочков квадрата
К
числу полезных и увлекательных
развлечений относится составление
фигур из семи кусочков квадрата,
разрезанного в соответствии с рис.3,
(а), причём при составлении заданных
фигур должны быть использованы все
семь кусочков, и они не должны налегать,
даже частично, друг на друга.
На
рис.4 приведены симметричные фигуры1.
Попробуйте сложить эти фигуры из частей
квадрата, изображённого на рис.3,(а).
Рис.4
Из
этих чертежей можно складывать и многие
другие фигуры (например, изображения
различных предметов, животных и т.п.).
Менее
распространённым вариантом игры
является составление фигур из кусочков
квадрата, изображённого на рис. 3,(b).
Магические квадраты
Магическим
«n2-квадратом»
назовём квадрат, разделённый на n2
клеток, заполненных первыми n2
натуральными числами так, что суммы
чисел, стоящих в любом горизонтальном
или вертикальном ряду, а также на любой
из диагоналей квадрата, равны одному
и тому же числу .
Если
одинаковы лишь суммы чисел, стоящих в
любом горизонтальном и вертикальном
ряду, то квадрат называется полумагическим.
16
|
|
| ||||||||||||||||||||||||||||||||||
Магический Кстати, | Существует | |||||||||||||||||||||||||||||||||||
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #