Двигатель совершает за 1 цикл полезную работу 500 дж и имеет кпд
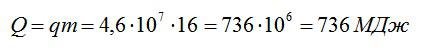
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Идеальная тепловая машина с КПД 55(%) за цикл работы получает от нагревателя 100 Дж. Какую полезную работу машина совершает за цикл? (Ответ дайте в джоулях.)
Под полезной работой понимается работа, которую совершила тепловая машина за цикл.
КПД тепловой машины можно найти по формуле: [eta=dfrac{A_text{ц}}{Q_{text{н}}}] Выразим работу, совершенную тепловой машиной за цикл: [A_text{ц}=eta cdot Q_{text{н}}] [A_text{ц}=0,55cdot100text{ Дж}=55text{ Дж}]
Ответ: 55
Тепловая машина за цикл работы получает от нагревателя количество теплоты, равное 100 Дж, и отдает холодильнику количество теплоты, равное 40 Дж. Чему равен КПД тепловой машины? (Ответ дайте в процентах.)
КПД тепловой машины можно найти по формуле: [eta=1-dfrac{Q_{text{х}}}{Q_{text{н}}}] [eta =1-dfrac{40text{ Дж}}{100text{ Дж}}=0,6=60%]
Ответ: 60
Тепловая машина за цикл совершает работу 50 Дж и отдает холодильнику количество теплоты, равное 100 Дж. Чему равен КПД тепловой машины? (Ответ дайте в долях единицы и округлите до сотых.)
КПД тепловой машины: [eta=1-dfrac{Q_{text{х}}}{Q_{text{н}}}] Зная работу тепловой машины за цикл и количество теплоты, отданное холодильнику, можно найти количество теплоты, принятое нагревателем: [A=Q_{text{н}}-Q_{text{х}}] [Q_{text{н}}=A+Q_{text{х}}] [Q_text{н}=50text{ Дж}+100text{ Дж}=150text{ Дж}] Найдем КПД тепловой машины: [eta=1-dfrac{100text{ Дж}}{150text{ Дж}}approx 0,33]
Ответ: 0,33
Тепловая машина с КПД 60(%) за цикл работы отдает холодильнику количество теплоты, равное 100 Дж. Какое количество теплоты за цикл машина получает от нагревателя? (Ответ дайте в джоулях.)
КПД тепловой машины можно найти по формуле: [eta=1-dfrac{Q_{text{х}}}{Q_{text{н}}}] Выразим отсюда количество теплоты, которое машина получает от нагревателя за цикл: [Q_{text{н}}=dfrac{Q_{text{х}}}{1-eta}] [Q_text{н} = dfrac{100text{ Дж}}{1-0,6}=250 text{ Дж}]
Ответ: 250
КПД идеальной тепловой машины, работающей по циклу Карно, равен (eta= 60%). Если температуру нагревателя увеличить в два раза, а температуру холодильника уменьшить в 2 раза, чему будет равен КПД тепловой машины? (Ответ дайте в процентах.)
КПД идеальной тепловой машины в первом случае: [eta_o=1-dfrac{T_{text{х}o}}{T_{text{н}o}}] Выразим отсюда отношение температуры холодильника к температуре нагревателя: [dfrac{T_{text{х}o}}{T_{text{н}o}}=1-0,6=0,4] Найдем КПД тепловой машины во втором случае: [eta=1-dfrac{T_{text{х}}}{T_{text{н}}},] где температура холодильника уменьшилась в два раза (T_{text{х}} = dfrac{T_{text{х}o}}{2} ), а температура нагревателя увеличилась в 2 раза (T_{text{н}} = 2T_{text{н}o}). [eta=1-dfrac{1}{4}cdotdfrac{T_{text{х}o}}{T_{text{н}o}}] [eta=1-dfrac{1}{4}cdot{0,4}=0,9=90%]
Ответ: 90
В некотором циклическом процессе КПД двигателя 50%, за цикл газ отдаёт холодильнику 50 Дж. Чему равна теплота, отданная от нагревателя рабочему телу?
“Досрочная волна 2019 вариант 1”
КПД вычисляется по формуле: [eta = 1-dfrac{Q_x}{Q_text{ н}}] Откуда теплота: [Q_text{ н}=dfrac{Q_x}{1-eta}=dfrac{50text{ Дж}}{1-0,5=100text{ Дж}}]
Ответ: 100
Если идеальная тепловая машина за цикл совершает полезную работу 50 Дж и отдает холодильнику 50 Дж, то каков ее КПД? (Ответ дайте в процентах.)
“Досрочная волна 2019 вариант 2”
КПД: [eta =dfrac{A}{A+Q_x}=dfrac{50text{ кДж}}{50text{ кДж}+50text{ кДж}}=0,5]
Ответ: 50
Источник
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Газ, совершающий цикл Карно, отдаёт холодильнику 70(%) теплоты, полученной от нагревателя. Температура нагревателя (T = 400) K. Найдите температуру холодильника. (Ответ дайте в кельвинах.)
Так как газ отдает 70(%) тепоты холодильнику, то только 30(%) идет на работу цикла.
Следовательно КПД равен (eta=30%). [eta=1-dfrac{T_{text{х}}}{T_{text{н}}}] Выразим температуру холодильника: [T_{text{х}}=T_{text{н}}cdot(1-eta)=400text{ К}cdot(1-0,3)=280 text{ К}]
Ответ: 280
В цикле Карно абсолютная температура нагревателя в 2,5 раза выше абсолютной температуры холодильника. Какая доля теплоты, полученной рабочим телом от нагревателя, передается холодильнику? (Ответ дайте в процентах.)
Из условия: [T_{text{п}}=2,5T_{text{х}}]
КПД в цикле Карно: [eta=1-dfrac{T_{text{х}}}{T_{text{н}}}] [eta = 1-dfrac{1T_{text{х}}}{2,5T_{text{х}}}=dfrac{1}{2,5}=0,6]
Следовательно, холодильнику передается теплоты: [1-eta=1-0,6=0,4]
Ответ: 40
Тепловая машина с КПД 40(%) за цикл работы отдает холодильнику 100 Дж. Какое количество теплоты за цикл машина получает от нагревателя? (Ответ дайте в джоулях, округлив до целых.)
КПД цикла можно найти по формуле: [eta=1-dfrac{Q_{text{х}}}{Q_{text{н}}}] Выразим количество теплоты, которое машина получает от нагревателя за цикл: [Q_{text{н}}=dfrac{Q_{text{х}}}{1-eta}] [Q_{text{н}}=dfrac{100text{ Дж}}{1-0,4} approx 167 text{ Дж}]
Ответ: 167
Температура холодильника тепловой машины 400 К, температура нагревателя на 600 К больше, чем у холодильника. Каков максимально возможный КПД машины? (Ответ дайте в процентах.)
Из условия: [T_{text{н}}=T_text{х}+400text{ К}] [T_{text{н}} = 600text{ К}+400text{ К}=1000text{ К}]
КПД в цикле Карно можно найти по формуле: [eta=1-dfrac{T_{text{х}}}{T_{text{н}}}] [eta = 1-dfrac{400text{ К}}{1000text{ К}}=0,6=60%]
Ответ: 60
Тепловая машина за один цикл совершает работу 20 Дж и отдаёт холодильнику количество теплоты 80 Дж. Температура нагревателя этой машины 600 К, а температура холодильника 300 К. Во сколько раз КПД идеальной тепловой машины, работающей при тех же температурах нагревателя и холодильника, больше КПД рассматриваемой тепловой машины?
КПД идеальной тепловой машины в цикле Карно можно найти по формуле: [eta_{max}=1-dfrac{T_{text{х}}}{T_{text{н}}}] [eta_{max} = 1-dfrac{300text{ К}}{600text{ К}}=1-0,5=0,5]
КПД рассматриваемой тепловой машины: [eta=dfrac{A_{text{цикл}}}{Q_{text{н}}}] Зная работу тепловой машины за цикл и количество теплоты, отданное холодильнику, можно найти количество теплоты, принятое нагревателем: [A_{text{цикл}}=Q_{text{н}}-Q_{text{х}}] [Q_{text{н}}=A_{text{цикл}}+Q_{text{х}}] [Q_{text{н}}=20text{ Дж}+80text{ Дж}=100 text{ Дж}] Найдем КПД рассматриваемой машины: [eta=dfrac{20text{ Дж}}{100text{ Дж}}=0,2] Найдем, во сколько раз КПД идеальной тепловой машины, работающей при тех же температурах нагревателя и холодильника, больше КПД рассматриваемой тепловой машины: [dfrac{eta_{max}}{eta}=frac{0,5}{0,2}=2,5]
Ответ: 2,5
Температура холодильника тепловой машины 800 К, температура нагревателя на 200 К больше, чем у холодильника. Каков максимально возможный КПД машины? (Ответ дайте в процентах.)
Из условия: [T_text{н}=T_text{х}+200text{ К}] [T_{text{н}}=800text{ К}+200text{ К}=1000text{ К}] КПД цикла Карно можно найти по формуле: [eta=1-dfrac{T_{text{х}}}{T_{text{н}}}] [eta =1-dfrac{800text{ Дж}}{1000text{ Дж}}=0,2]
Ответ: 20
Тепловая машина с КПД 30(%) за цикл работы отдаёт холодильнику количество теплоты, равное 50 Дж. Какое количество теплоты машина получает за цикл от нагревателя? (Ответ дайте в джоулях, округлив до десятых.)
КПД тепловой машины можно найти по формуле: [eta=1-dfrac{Q_{text{х}}}{Q_{text{н}}}] Выразим количество теплоты, которое машина получает за цикл от нагревателя: [Q_{text{н}}=dfrac{Q_{text{х}}}{1-eta}] [Q_text{н} =dfrac{50text{ Дж}}{0,7}=71,4 text{ Дж}]
Ответ: 71,4
Источник
У нас уже была внутренняя энергия и первое начало термодинамики, а сегодня разберемся с задачами на КПД теплового двигателя. Что поделать: праздники праздниками, но сессию ведь никто не отменял.
Присоединяйтесь к нам в телеграме и получайте полезную рассылку каждый день. А приступая к практике, не забывайте держать под рукой памятку по задачам и полезные формулы.
Задачи по физике на КПД теплового двигателя
Задача на вычисление КПД теплового двигателя №1
Условие
Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.
Решение
Коэффициент полезного действия можно вычислить как отношение полезной работы и полного количества теплоты, выделенного спиртовкой:
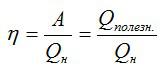
Полезная работа в данном случае – это эквивалент количества теплоты, которое пошло исключительно на нагрев. Его можно вычислить по известной формуле:
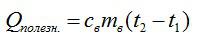
Полное количество теплоты вычисляем, зная массу сгоревшего спирта и его удельную теплоту сгорания.
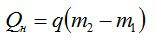
Подставляем значения и вычисляем:
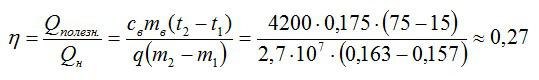
Ответ: 27%
Задача на вычисление КПД теплового двигателя №2
Условие
Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.
Решение
Найдем общее количество теплоты, которое произвел двигатель:
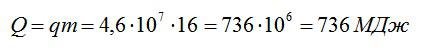
Теперь можно рассчитать КПД:
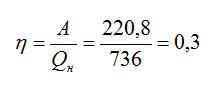
Или, умножая на 100, получаем значение КПД в процентах:
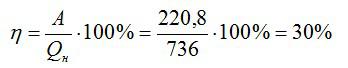
Ответ: 30%.
Задача на вычисление КПД теплового двигателя №3
Условие
Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.
Решение
КПД идеальной тепловой машины:
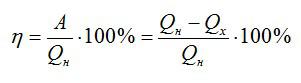
По условию:
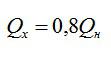
Вычислим сначала работу, а затем КПД:
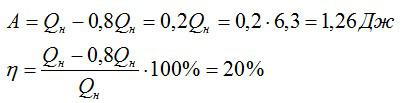
Ответ: 20%; 1,26 Дж.
Задача на вычисление КПД теплового двигателя №4
Условие
На диаграмме изображен цикл дизельного двигателя, состоящий из адиабат 1–2 и 3–4, изобары 2–3 и изохоры 4–1. Температуры газа в точках 1, 2, 3, 4 равны T1 , T2 , T3 , T4 соответственно. Найдите КПД цикла.
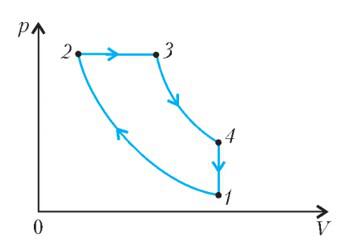
Решение
Проанализируем цикл, а КПД будем вычислять через подведенное и отведенное количество теплоты. На адиабатах тепло не подводится и не отводится. На изобаре 2 – 3 тепло подводится, объем растет и, соответственно, растет температура. На изохоре 4 – 1 тепло отводится, а давление и температура падают.
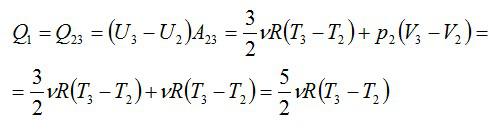
Аналогично:
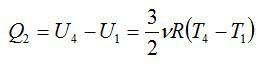
Получим результат:
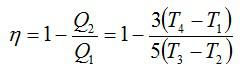
Ответ: См. выше.
Задача на вычисление КПД теплового двигателя №5
Условие
Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.
Решение
Запишем формулу для КПД:
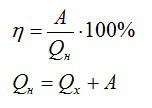
Отсюда:
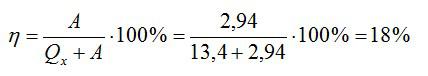
Ответ: 18%
Вопросы на тему тепловые двигатели
Вопрос 1. Что такое тепловой двигатель?
Ответ. Тепловой двигатель – это машина, которая совершает работу за счет энергии, поступающей к ней в процессе теплопередачи. Основные части теплового двигателя: нагреватель, холодильник и рабочее тело.
Вопрос 2. Приведите примеры тепловых двигателей.
Ответ. Первыми тепловыми двигателями, получившими широкое распространение, были паровые машины. Примерами современного теплового двигателя могут служить:
- ракетный двигатель;
- авиационный двигатель;
- газовая турбина.
Вопрос 3. Может ли КПД двигателя быть равен единице?
Ответ. Нет. КПД всегда меньше единицы (или меньше 100%). Существование двигателя с КПД равным единице противоречит первому началу термодинамики.
КПД реальных двигателей редко превышает 30%.
Вопрос 4. Что такое КПД?
Ответ. КПД (коэффициент полезного действия) – отношение работы, которую совершает двигатель, к количеству теплоты, полученному от нагревателя.
Вопрос 5. Что такое удельная теплота сгорания топлива?
Ответ. Удельная теплота сгорания q – физическая величина, которая показывает, какое количество теплоты выделяется при сгорании топлива массой 1 кг. При решении задач КПД можно определять по мощности двигателя N и сжигаемому за единицу времени количеству топлива.
Задачи и вопросы на цикл Карно
Затрагивая тему тепловых двигателей, невозможно оставить в стороне цикл Карно – пожалуй, самый знаменитый цикл работы тепловой машины в физике. Приведем дополнительно несколько задач и вопросов на цикл Карно с решением.
Цикл (или процесс) Карно – это идеальный круговой цикл, состоящий из двух адиабат и двух изотерм. Назван так в честь французского инженера Сади Карно, который описал данный цикл в своем научном труде «О движущей силе огня и о машинах, способных развивать эту силу» (1894).
Задача на цикл Карно №1
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 73,5 кДж. Температура нагревателя t1 =100° С, температура холодильника t2 = 0° С. Найти КПД цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.
Решение
Рассчитаем КПД цикла:
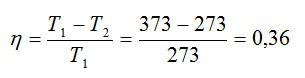
С другой стороны, чтобы найти количество теплоты, получаемое машиной, используем соотношение:
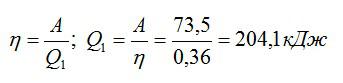
Количество теплоты, отданное холодильнику, будет равно разности общего количества теплоты и полезной работы:
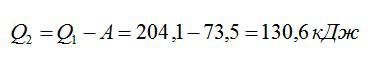
Ответ: 0,36; 204,1 кДж; 130,6 кДж.
Задача на цикл Карно №2
Условие
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла.
Решение
Формула для КПД цикла Карно:
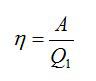
Здесь A – совершенная работа, а Q1 – количество теплоты, которое понадобилось, чтобы ее совершить. Количество теплоты, которое идеальная машина отдает холодильнику, равно разности двух этих величин. Зная это, найдем:
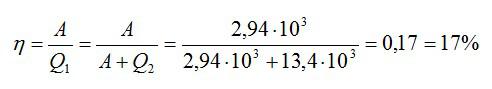
Ответ: 17%.
Задача на цикл Карно №3
Условие
Изобразите цикл Карно на диаграмме и опишите его
Решение
Цикл Карно на диаграмме PV выглядит следующим образом:

- 1-2. Изотермическое расширение, рабочее тело получает от нагревателя количество теплоты q1;
- 2-3. Адиабатическое расширение, тепло не подводится;
- 3-4. Изотермическое сжатие, в ходе которого тепло передается холодильнику;
- 4-1. Адиабатическое сжатие.
Ответ: см. выше.
Вопрос на цикл Карно №1
Сформулируйте первую теорему Карно
Ответ. Первая теорема Карно гласит: КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела.
Вопрос на цикл Карно №2
Может ли коэффициент полезного действия в цикле Карно быть равным 100%?
Ответ. Нет. КПД цикла карно будет равен 100% только в случае, если температура холодильника будет равна абсолютному нулю, а это невозможно.
Если у вас остались вопросы по теме тепловых двигателей и цикла Карно, вы можете смело задавать их в комментариях. А если нужна помощь в решении задач или других примеров и заданий, обращайтесь в профессиональный студенческий сервис.
Источник
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 68.8%
Ответом к заданию 9 по физике может быть целое число или конечная десятичная дробь.
Задачи для практики
Задача 1
Газ, находящийся в теплоизолированном цилиндре с подвижным поршнем, получает от нагревателя количество теплоты, равное 200 Дж. Поршень при этом, преодолевая сопротивление 800 Н, переместился на 10 см. Насколько изменилась внутренняя энергия газа? В ответе запишите на сколько (Дж).
Решение
Дано:
$Q=200$Дж
$F=800$Н
$∆x=0.1$м
$∆U-?$
Решение:
Запишем I начало термодинамики: $Q=A+∆U$(1), где $A=F·∆x$(2) – работа газа, $∆U$ – изменение внутренней энергии газа. Тогда из (1) с учетом (2) имеем: $∆U=Q-A=Q-F·∆x=200-800·0.1=200-80=120$Дж.
Ответ: 120
Показать решение
Полный курс
Задача 2
В цилиндре под поршнем находится 2 кг воздуха (M = 0,029 кг/моль) при 20◦С под давлением 1 МПа. Чему равна работа при изобарном нагревании воздуха до 100◦С? Ответ выразите в (кДж), округлив до десятых.
Решение
Дано:
$m=2$кг
$μ=0.029$кг/моль
$t_1=20°C$
$t_2=100°C$
$p=10^6$Па
$R=8.31$Дж/моль·К
$A-?$
Решение:
Работа воздуха определяется выражением: $A=p·∆V$(1), где $p$ – давление, $∆V$ – изменение объема цилиндра (воздуха).
Запишем уравнение Менделеева-Клайперона: $p∆V={m}/{μ}R∆T$(2), учитывая, что $∆T=∆t=t_2-t_1=100°C-20°C=80K$.
Подставим (2) в (1), получим: $A=p·∆V={m}/{μ}R∆T={2·8.31·80}/{0.029}=45848.275=45.8$кДж.
Ответ: 45.8
Показать решение
Полный курс
Задача 3
Температуры нагревателя и холодильника у идеального двигателя соответственно равны 427◦C и 27◦C . Какую работу совершает двигатель за один цикл, если он получает от нагревателя в течение цикла количество теплоты равное 7000 Дж? Ответ выразите в (кДж).
Решение
Дано:
$t_н=427°C$
$t_х=27°C$
$Q_н=7000$Дж
$A-?$
Решение:
КПД двигателя определяется выражением: $η={T_н-T_x}/{T_н}={A}/{Q_н}$(1), где $T_н=t_н+273K=427+273=700K; T_x=t_x+273=27+273=300K$, абсолютные температуры нагревателя и холодильника. Из (1) выразим работу двигателя А: $A={(T_н-T_x)·Q_н}/{T_н}={(700-300)·7000}/{700}=4000=4$кДж.
Ответ: 4
Показать решение
Полный курс
Задача 4
Какую работу совершит газ, расширяясь при постоянном давлении 304 кПа от объёма 3 л до объёма 18 л? Ответ выразите в (кДж).
Решение
Дано:
$p=304·10^3$Па
$V_1=3·10^{-3}м^3$
$V_2=18·10^{-3}м^3$
$A-?$
Решение:
Работа газа определяется выражением: $A=p·∆V=p·(V_2-V_1)=304·10^3·(18·10^{-3}-3·10^{-3})=304·10^3·15·10^{-3}=4560=4.56$кДж.
Ответ: 4.56
Показать решение
Полный курс
Задача 5
В закрытом сосуде под поршнем находится водяной пар при температуре 100◦С под давлением 40 кПа. Каким станет давление пара в сосуде, если объём пара в нём изотермически уменьшить в 1,5 раза за счёт движения поршня? Ответ выразите в (кПа).
Решение
Дано:
$T_1=100°С$
$P_1=40$кПа
$T=const$
$V_2={V_1}/{1.5}$
$P_2-?$
Решение:
По закону Менделеева-Клайперона $P_1·V_1=P_2·V_2⇒P_2={P_1·V_1}/{V_2}=40·1.5=60$кПа.
Ответ: 60
Показать решение
Полный курс
Задача 6
Тепловая машина имеет КПД 25%. Найдите среднюю мощность передачи теплоты холодильнику, если рабочее тело машины за 10 с получает от нагревателя 30 кДж теплоты. Ответ выразите в (кВт).
Решение
Дано:
$η=0.25$
$t=10c$
$Q_н=30$кДж
$P_x-?$
Решение:
$P_н={Q_н}/{t}={30}/{10}=3$кВт.
$η={P_н-P_x}/{P_н}·100$.
$P_x=P_н-η·P_н=3-0.75=2.25$кВт.
Ответ: 2.25
Показать решение
Полный курс
Задача 7
КПД двигателя внутреннего сгорания равен 60%. Определите температуру в камере сгорания двигателя, если температура струи, выходящей из его сопла, составляет 727◦С. Ответ выразить в (K).
Решение
Дано:
$η=0.6$
$T_{вых}=727+273=1000К$
$T_н-?$
Решение:
$η={T_н-T_x}/{T_н}$ для тепловой машины определяем $T_н$.
$0.6={T_н-1000}/{T_н}; T_н={1000}/{0.4}=2500K$.
Ответ: 2500
Показать решение
Полный курс
Задача 8
У работающего по циклу Карно теплового двигателя температура нагревателя 400 К, а температура холодильника 150 К. Найдите коэффициент полезного действия этого двигателя. Ответ выразите в (%).
Решение
Дано:
$T_н=400K$
$η-?$
$T_x=150K$
Решение:
Для цикла Карно справедливо уравнение $η={T_н-T_x}/{T_н}·100%={400-150}/{400}·100%=62.5%$
Ответ: 62.5
Показать решение
Полный курс
Задача 9
Температура нагревателя 177◦С. Определите температуру холодильника, если известно, что коэффициент полезного действия этого двигателя равен 45%. Ответ выразите в (К).
Решение
Дано:
$T_н=177°C$
$η=45%$
$T_x-?$
Решение:
Из теории о теплообмене $η={T_н-T_x}/{T_н}·100%$
$0.45={177-T_x}/{177}$. Нельзя, т.к. $T_н=177+273=450K$
$0.45={450-T_x}/{450}⇒T_x=247.5K$
Ответ: 247.5
Показать решение
Полный курс
Задача 10
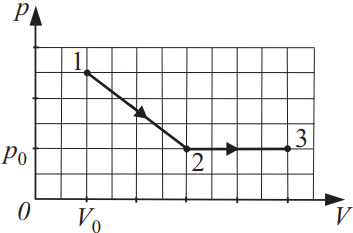
На рисунке показана зависимость давления идеального газа от его объёма при переходе из состояния 1 в состояние 2, а затем в состояние 3. Найдите, чему равно отношение работ газа ${A_{12}}/{A_{23}}$.
Решение
Дано:
${A_{12}}/{A_{23}}-?$
Решение:
Воспользуемся соотношением площадей под графиком ${S_{12}}/{S_{23}}={14}/{8}=1.75$.
Ответ: 1.75
Показать решение
Полный курс
Задача 11
Тепловая машина с КПД 60% за цикл работы отдаёт холодильнику 100 Дж теплоты. Какое количество теплоты за цикл получает машина от нагревателя? Ответ выразите в (Дж).
Решение
Дано:
$η=60%$
$Q_x=100$Дж
$Q_н-?$
Решение:
1) Из теории о тепловых машинах $η={Q_н-Q_x}/{Q_н}·100%$.
$100=Q_н·0.4$
$0.6=1-{100}/{Q_н}$
$Q_н=250$Дж
Ответ: 250
Показать решение
Полный курс
Задача 12
Идеальный газ совершил работу 100 Дж и отдал при этом количество теплоты 300 Дж. Как изменилась при этом внутренняя энергия? В ответе запишите на сколько уменьшилась (Дж).
Решение
Дано:
$A=100$Дж
$Q=-300$Дж
Решение:
По первому началу термодинамики $∆U=A+Q=100+300=400$Дж. Газ отдает тепло и совершает $А$, $∆U$ – уменьшается.
Ответ: 400
Показать решение
Полный курс
Задача 13
Рабочее тело тепловой машины за один цикл получает от нагревателя теплоту 1000 Дж. Температура нагревателя 500 К, температура холодильника 200 К. Какую работу совершает рабочее тело за один цикл? Ответ выразите в (Дж).
Решение
Дано:
$Q_н=1000$Дж
$T_н=500$К
$T_x=200$К
Решение:
$A=Q_н-Q_x$
$η={T_н-T_x}/{T_н}={Q_н-Q_x}/{Q_н}$ по формуле из основы теплообмена.
$A={(T_н-T_x)Q_н}/{T_н}={300·1000}/{500}=600$Дж.
Ответ: 600
Показать решение
Полный курс
Задача 14
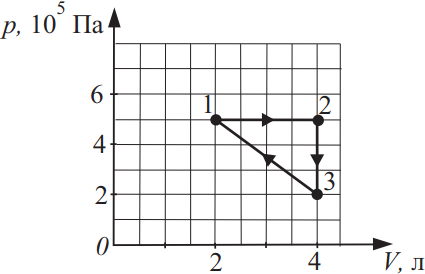
Вычислите работу идеального газа при совершении им кругового процесса, изображённого на рисунке. Ответ выразите в (Дж).
Решение
Дано:
$А-?$
Решение:
Из графика очевидно: $A=A_{12}+A_{23}+A_{31}$
$A_{23}=0$, т.к. нет изменения $V$.
$A_{12}=p∆V=5·10^5·2·10^{-3}=10^3$
$A_{31}={1}/{2}(2·10^5+5·10^5)·2·10^{-3}=-7·10^2$
$A=A_{12}-A_{31}=1000-700=300$Дж.
Ответ: 300
Показать решение
Полный курс
Задача 15
В некотором процессе газ отдал окружающей среде количество теплоты, равное 10 кДж. При этом внутренняя энергия газа увеличилась на 30 кДж. Определите работу, которую совершили внешние силы, сжав газ. Ответ выразить в (кДж).
Решение
Дано:
$Q=10$кДж
$∆U=30$кДж
$A-?$
Решение:
Первое начало термодинамики говорит о том, что количество $Q$ сообщенное системе, идет на приращение внутренней энергии и на совершении работы над внешними телами $Q=∆U+A$
$A=Q-(-∆U)=10+30=40$кДж
Ответ: 40
Показать решение
Полный курс
Задача 16
Двигатель внутреннего сгорания совершил работу, равную 27,6 МДж, и израсходовал при этом 3 л бензина. Вычислите КПД двигателя. Удельная теплота сгорания бензина равна 44 МДж/кг. Плотность бензина равна 700 кг/м3. Ответ округлите до целого. Ответ выразите в (%).
Решение
Дано:
$A_n=27.6$МДж
$m_б=ρ_б·v_б$
$v_б=3$л
$r=44$МДж/кг
$ρ_б=700$кг/м$^3$
$η-?$
Решение:
$η={A_п}/{A_з}$ – полезная и затраченная работа.
$A_з=Q$(сгорание бензина)$=r·m_б=r·ρ_б·v_б$.
$η={27.6·10^6}/{44·10^6·100·3·10^{-3}}·100%=30%$
Ответ: 30
Показать решение
Полный курс
Задача 17
В цилиндре под поршнем находится гелий. Газ расширился при постоянном давлении, совершив работу 3 кДж. Какое количество теплоты сообщили газу? Ответ выразите в (кДж).
Решение
Дано:
$A=3·10^3$Дж
$i=3$
$Q-?$
Решение:
Запишем I начало термодинамики для изобарного процесса (p=const): $Q=A+∆U$(1), где $A=p·∆V$(2), $∆U={i}/{2}υR∆T$(3) – изменения внутренней энергии гелия. Исходя из уравнения Менделеева-Клайперона: $p·∆V=υR∆T$(4), $∆U={i}/{2}p·∆V={i}/{2}A$(5). Подставим (5) в (1): $Q=A+{i}/{2}A=A(1+{i}/{2})$(6). Подставим числовые значения в (6): $Q=3·10^3(1+{3}/{2})=7.5кДж$
Ответ: 7.5
Показать решение
Полный курс
Задача 18
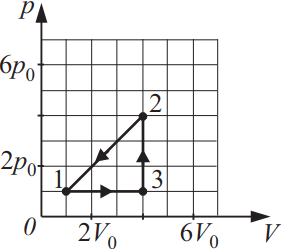
Работа газа в круговом процессе равна 900 кДж. Рассчитайте значение объёма V0, если давление p0 = 105 Па. Ответ выразите в (м3).
Решение
Дано:
$p_0=10^5$Па
$A=9·10^5$Дж
$V_0-?$
Решение:
Работа газа в термодинамике численно равна площади фигуры кругового процесса. Найдем эту площадь: $A={(p_2-p_1)·(V_3-V_1)}/{2}$(1)
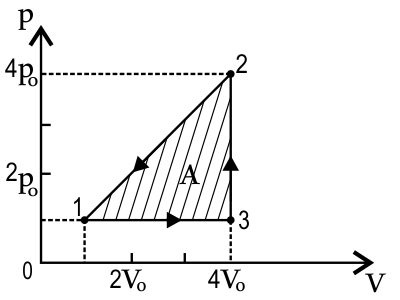
Подставим: $p_2=4p_0; p_1=p_0; V_3=4V_0; V_1=V_0$
$A={(4p_0-p_0)·(4V_0-V_0)}/{2}$
$2A=3p_0·3V_0$
$2A=9p_0V_0$
$V_0={2A}/{9p_0}$(2)
Подставим числовые значения в (2): $V_0={2·9·10^5}/{9·10^5}=2м^3$
Ответ: 2
Показать решение
Полный курс
Задача 19
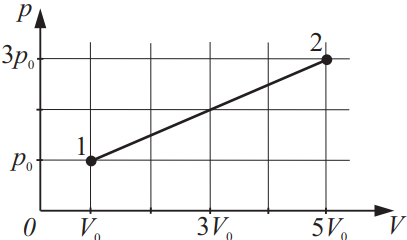
Рассчитайте работу газа при переходе из состояния 1 в состояние 2, если давление p0 = 105 Па, а объём V0 = 1 м3. Ответ выразите в (кДж).
Решение
Дано:
$p_0=10^5$Па
$V_0=1м^3$
$p_1=p_0$
$V_1=V_0$
$p_2=3p_0$
$V_2=5V_0$
$A_{12}-?$
Решение:
Поскольку работа газа в термодинамике численно равна площади под графиком, т.е. площади трапеции.
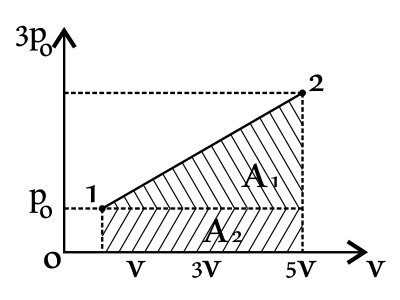
Тогда имеем: $A_{12}=A-1+A_2={(3p_0-p_0)·(5V_0-V_0)}/{2}+(p_0-0)·(5V_0-V_0)={2p_0·4V_0}/{2}+p_0·4V_0=4p_0V_0+4p_0V_0=8p_0V_0$(1)
Подставим числовые значения в (1): $A_{12}=8·10^5·1=8·10^5=800$кДж.
Ответ: 800
Показать решение
Полный курс
Задача 20
Температура нагревателя идеальной тепловой машины в два раза больше температуры холодильника. Каков термический КПД цикла? Ответ выразите в (%).
Решение
Дано:
$T_н=2T$
$T_x=T$
$η-$
Решение:
КПД цикла определяется по формуле: $η={T_н-T_x}/{T_н}·100%$(1), $T_н$ – температура нагревателя, $T_x$ – температура холодильника.
$η={2T-T}/{2T}·100%={T·100%}/{2T}=50%$
Ответ: 50
Показа
