Цикл карно коэффициент полезного действия тепловой машины

В термодинамике цикл Карно́ или процесс Карно́ — это идеальный[1]круговой процесс, состоящий из двух адиабатных и двух изотермических процессов[2]. В процессе Карно термодинамическая система выполняет механическую работу за счёт обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником[3].

Цикл Карно назван в честь французского учёного и инженера Сади Карно, который впервые его описал в своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу» в 1824 году[4][5].

Поскольку идеальные процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному процессу Карно только с большей или меньшей степенью точности.

Коэффициент полезного действия (КПД) любой тепловой машины не может превосходить КПД идеальной тепловой машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника[6]. По этой причине, позволяя оценить верхний предел КПД тепловой машины, цикл Карно важен для теории тепловых машин. В то же время КПД цикла Карно настолько чувствителен к отклонениям от идеальности (потерям на трение), что данный цикл никогда не применяли в реальных тепловых машинах[K 1][8].

Описание цикла Карно[править | править код]

Рис. 1. Цикл Карно в координатах T—S

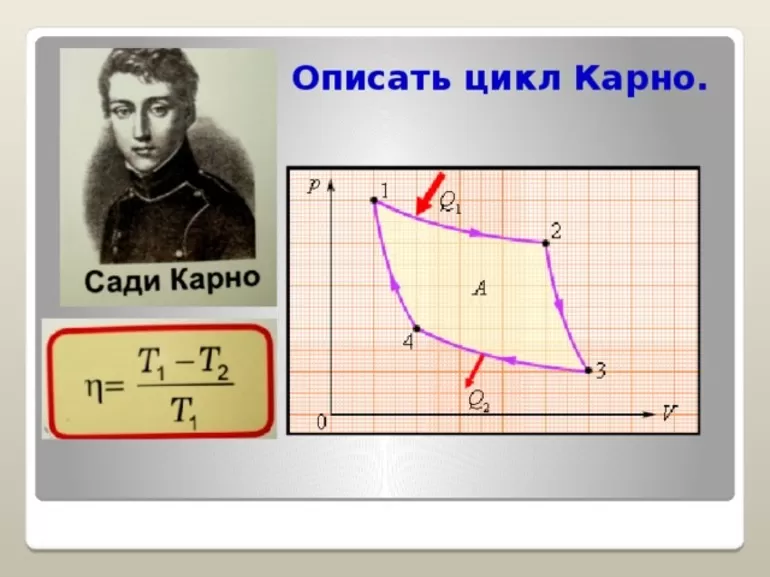
Рис. 2. Цикл Карно в координатах p—V

Рис. 3. Цикл Карно на термодинамической поверхности идеального газа

Пусть тепловая машина состоит из нагревателя с температурой , холодильника с температурой и рабочего тела.

Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах (температура) и (энтропия).

1. Изотермическое расширение (на рис. 1 — процесс A→B). В начале процесса рабочее тело имеет температуру , то есть температуру нагревателя. При расширении рабочего тела его температура не падает за счет передачи от нагревателя количества теплоты , то есть расширение происходит изотермически (при постоянной температуре) . При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.

2. Адиабатическое расширение (на рис. 1 — процесс B→C). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника , тело совершает механическую работу, а энтропия остаётся постоянной.

3. Изотермическое сжатие (на рис. 1 — процесс C→D). Рабочее тело, имеющее температуру , приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты . Над телом совершается работа, его энтропия уменьшается.

4. Адиабатическое сжатие (на рис. 1 — процесс D→A). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.

Обратный цикл Карно[править | править код]

В термодинамике холодильных установок и тепловых насосов рассматривают обратный цикл Карно, состоящий из следующих стадий[9][10]: адиабатического сжатия за счёт совершения работы (на рис. 1 — процесс C→B); изотермического сжатия с передачей теплоты более нагретому тепловому резервуару (на рис. 1 — процесс B→A); адиабатического расширения (на рис. 1 — процесс A→D); изотермического расширения с отводом теплоты от более холодного теплового резервуара (на рис. 1 — процесс D→C).

КПД тепловой машины Карно[править | править код]

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику

Отсюда коэффициент полезного действия тепловой машины Карно равен

Первая и вторая теоремы Карно[править | править код]

Из последнего выражения следует, что КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела. Этот результат составляет содержание первой теоремы Карно[11]. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.

Поэтому максимальный КПД любой тепловой машины не может превосходить КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Это утверждение называется второй теоремой Карно[12][13]. Оно даёт верхний предел КПД любой тепловой машины и позволяет оценить отклонение реального КПД от максимального, то есть потери энергии вследствие неидеальности тепловых процессов.

Связь между обратимостью цикла и КПД[править | править код]

Для того чтобы цикл был обратимым, в нём должна быть исключена передача теплоты при наличии разности температур, иначе нарушается условие адиабатичности процесса. Поэтому передача теплоты должна осуществляться либо в изотермическом процессе (как в цикле Карно), либо в эквидистантном процессе (обобщённый цикл Карно или, для примера, его частный случай Цикл Брайтона). Для того чтобы менять температуру рабочего тела от температуры нагревателя до температуры холодильника и обратно, необходимо использовать либо адиабатические процессы (они идут без теплообмена и, значит, не влияют на энтропию), либо циклы с регенерацией тепла при которых нет передачи тепла при разности температур. Мы приходим к выводу, что любой обратимый цикл может быть сведён к циклу Карно.

Примером обратимого цикла, не являющегося циклом Карно, но интегрально совпадающим с ним, является идеальный цикл Стирлинга: в двигателе Стирлинга добавлен регенератор, обеспечивающий полное приближение цикла к циклу Карно с достижением обратимости и тех же величин КПД[14]. Возможны и другие идеальные циклы, в которых коэффициент полезного действия определяется по той же формуле, что и для циклов Карно и Стирлинга, например цикл Эрикссона (англ.)русск., состоящий из двух изобар и двух изотерм[14].

Если же в цикле возникает передача теплоты при наличии разности температур, а таковыми являются все технические реализации термодинамических циклов, то цикл утрачивает свойство обратимости. Иначе говоря, посредством отведённой в цикле механической работы становится невозможным получить исходную теплоту. КПД такого цикла будет всегда меньше, чем КПД цикла Карно.

См. также[править | править код]

Термодинамические циклы
Первое начало термодинамики
Второе начало термодинамики
Термодинамическая энтропия
Термодинамические потенциалы

Комментарии[править | править код]

↑ В реальных тепловых машинах цикл Карно не используют, поскольку практически невозможно осуществить процессы изотермического сжатия и расширения. Кроме того, полезная работа цикла, представляющая собой алгебраическую сумму работ во всех четырех составляющих цикл частных процессах, даже в идеальном случае полного отсутствия потерь мала по сравнению с работой в каждом из частных процессов, то есть мы имеем дело с обычной ситуацией, когда итоговый результат представляет собой малую разность больших величин. Применительно к математическим вычислениям это означает высокую отзывчивость результата даже на небольшие вариации значений исходных величин, а в рассматриваемом нами случае соответствует высокой чувствительности полезной работы цикла Карно и его КПД к отклонениям от идеальности (потерям на трение). Эта связь с отклонениями от идеальности настолько велика, что с учетом всех потерь полезная работа цикла Карно приближается к нулю[7].

Примечания[править | править код]

↑ То есть без потерь, в первую очередь на трение.
↑ Карно цикл // Италия — Кваркуш. — М. : Советская энциклопедия, 1973. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 11).
↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 94.
↑ Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. — Paris: Gauthier-Villars, Imprimeur-Libraire, 1878. — 102 p. (фр.)
↑ Второе начало термодинамики. (Работы Сади Карно — В. Томсон — Кельвин — Р. Клаузиус — Л. Больцман — М. Смолуховский) / Под. ред. А. К. Тимирязева. — Москва—Ленинград: Государственное технико-теоретическое издательство, 1934. — С. 17—61.
↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 113—114.
↑ Бэр Г. Д., Техническая термодинамика, 1977, с. 112.
↑ Кинан Дж., Термодинамика, 1963, с. 93.
↑ Николаев Г. П., Лойко А. Э., Техническая термодинамика, 2013, с. 172.
↑ Бахшиева Л. Т. и др., Техническая термодинамика и теплотехника, 2008, с. 148.
↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 95.
↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 113.
↑ Румер Ю. Б., Рывкин М. Ш., Термодинамика, статистическая физика и кинетика, 2000, с. 35.
↑ 1 2 Крестовников А. Н., Вигдорович В. Н., Химическая термодинамика, 1973, с. 63.

Литература[править | править код]

Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. — Paris: Gauthier-Villars, Imprimeur-Libraire, 1878. — 102 p. (фр.)
Бахшиева Л. Т., Кондауров Б. П., Захарова А. А., Салтыкова В. С. Техническая термодинамика и теплотехника / Под ред. проф А. А. Захаровой. — 2-е изд., испр. — М.: Академия, 2008. — 272 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-4999-1.
Бэр Г. Д. Техническая термодинамика. — М.: Мир, 1977. — 519 с. (недоступная ссылка)
Кинан Дж. Термодинамика / Пер с англ. А. Ф. Котина под ред. М. П. Вукаловича. — М.—Л.: Госэнергоиздат, 1963. — 280 с.
Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 3-е, доп. — М.: Наука, 1976. — 584 с. — («Теоретическая физика», том V).
Крестовников А. Н., Вигдорович В. Н. Химическая термодинамика. — 2-е изд., испр. и доп. — М.: Металлургия, 1973. — 256 с.
Николаев Г. П., Лойко А. Э. Техническая термодинамика. — Екатеринбург: УрФУ, 2013. — 227 с.
Румер Ю. Б., Рывкин М. Ш. Термодинамика, статистическая физика и кинетика. — 2-е изд., испр. и доп. — Новосибирск: Изд-во Носиб. ун-та, 2000. — 608 с. — ISBN 5-7615-0383-2.
Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.
Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика. — 5 изд., испр.. — М.: ФИЗМАТЛИТ, 2005. — 544 с. — ISBN 5-9221-0601-5.

Источник

Краткая биография

Николя Леонард Сади Карно, сын высокопоставленного военачальника Лазаря Николая Маргарита Карно, родился в Париже в 1796 году. Его отец ушёл из армии в 1807 году, чтобы обучить Николаса и его брата Ипполита — оба получили широкое домашнее образование, включающее:

науку;
искусство;
иностранные языки;
музыку.

В 1812 году 16-летний Николас Карно был принят в Высшую политехническую школу в Париже. Его учителями были Джозеф Луи Гей-Люссак, Симеон Дени Пуассон и Андре-Мари Ампер, а сокурсниками — будущие учёные Клод-Луи Навье и Гаспар-Гюстав Кориолис. Во время учёбы в школе Карно проявил особый интерес к теории газов и решению задач промышленной инженерии. После окончания университета он поступил во французскую армию в качестве военного инженера и прослужил до 1814 года.

Освободившись от ограничений военной жизни, Карно начал широкий спектр исследований, которые продолжались, несмотря на многочисленные перерывы, до само́й смерти. В дополнение к частным занятиям он посещал курсы:

в Сорбонне;
Коллеж де Франс.
в Школе шахт;
в Консерватории искусств.

В последней он стал другом Николаса Клемента, который преподавал курс прикладной химии, а затем занимался важными исследованиями паровых двигателей и теории газов.

Одним из особых интересов Карно было промышленное развитие, которое он изучал во всех его аспектах. Он часто посещал фабрики и мастерские, читал новейшие теории политической экономии и оставлял в своих заметках подробные предложения по таким актуальным проблемам, как налоговая реформа. Помимо этого, его деятельность и способности охватили математику и изобразительное искусство.

В 1821 году Карно прервал учёбу, чтобы провести несколько недель со своим отцом и братом в Магдебурге. По-видимому, именно после этого визита он снова в Париже начал концентрироваться на проблемах парового двигателя. 12 июня 1824 года была опубликована его книга «Отражение в чистоте и весе».

После публикации Карно продолжил исследования, выводы из которых сохранились в его рукописных заметках. Однако реорганизация корпуса Генерального штаба вынудила Карно вернуться на службу в 1827 году в звании капитана. После менее чем годовой работы в качестве военного инженера Карно ушёл в отставку навсегда и вернулся в Париж. Он снова сосредоточил своё внимание на проблемах конструкции двигателя и теории тепла.

В 1831 году Карно начал исследовать физические свойства газов и паров, особенно связь между температурой и давлением. Однако в июне 1832 года он заболел скарлатиной. За этим последовала «мозговая лихорадка», которая настолько подорвала его хрупкое здоровье, что 24 августа 1832 года он стал жертвой эпидемии холеры и умер в течение дня, в возрасте 36 лет. Согласно обычаю, его личные вещи, включая почти все его бумаги, были сожжены.

Работы учёного

Самая ранняя из основных рукописей написана, вероятно, в 1823 году и озаглавлена «Поиск формулы для представления движущей силы водяного пара». Как видно из названия, это была попытка найти математическое выражение для движущей силы, производимой паром. Явно стремясь найти общее решение, охватывающее все типы паровых двигателей, Карно сократил их работу до трёх основных этапов:

изотермическое расширение при подаче пара в цилиндр;
адиабатическое расширение;
изотермическое сжатие в конденсаторе.

Эссе как по методам, так и по целям похоже на многие статьи, опубликованные между 1818 и 1824 годами такими учёными, как Хашетт, Навье, Пети и Комбес. Работа Карно, однако, отличается своим тщательным, чётким анализом используемых единиц и концепций и тем, что он использует как адиабатическую рабочую стадию, так и изотермическую стадию. Отточенный характер, в отличие от его грубых заметок, делало её предназначенной для публикации, хотя она оставалась неизвестной в рукописи до 1966 года.

«Рефлексионы» (единственное произведение, опубликованное Карно за всю его жизнь) появилось в 1824 году как скромное эссе из 118 страниц. После краткого обзора промышленного, политического и экономического значения парового двигателя Карно поднял две проблемы, которые, по его мнению, помешали дальнейшему развитию как полезности, так и теории паровых двигателей:

Существует ли установленный предел для движущей силы тепла и, следовательно, для улучшения паровых двигателей?
Есть ли агенты предпочтительнее пара в производстве этой движущей силы?

Обе проблемы были своевременными и, хотя французские инженеры исследовали их в течение десятилетия, не было принято общепринятых решений. В отсутствии чёткой концепции эффективности предлагаемые конструкции паровых двигателей оценивались в основном по практичности, безопасности и экономии топлива.

Некоторые инженеры считали воздух, углекислоту и спирт лучшим рабочим веществом, чем пар. Обычным подходом к этим проблемам было либо эмпирическое исследование расхода топлива и выходной мощности отдельных двигателей, либо применение математической теории газов к абстрактным операциям конкретного типа двигателя. В своём выборе проблем Карно был твёрд в этой инженерской традиции, однако его метод был радикально новым и являлся сутью его вклада в науку о тепле.

Предыдущая работа над паровыми машинами, как видел Карно, провалилась из-за отсутствия достаточно общей теории, применимой ко всем тепловым двигателям и основанной на установленных принципах. В качестве основы своего исследования Карно тщательно изложил три предпосылки. Первой была невозможность вечного движения — принцип, который долгое время предполагался в механике. В своей второй предпосылке Карно использовал калорийную теорию тепла, которая, несмотря на некоторую оппозицию, была принятой и самой развитой, доступной теорией тепла.

Принципы работы цикла Карно

Этот теоретический идеальный круговой термодинамический цикл был предложен французским физиком Сади Карно в 1824 году. Он обеспечивал максимально возможный предел эффективности для любого классического термодинамического двигателя во время преобразования тепла в работу или, наоборот, эффективность системы охлаждения при создании разницы температур при приложении работы к системе. Фактический термодинамический цикл является теоретической конструкцией.

Каждая термодинамическая система существует в определённом состоянии. Когда система проходит через ряд различных явлений и, наконец, возвращается в исходное состояние, говорят, что произошёл термодинамический цикл. В процессе прохождения этого цикла система может выполнять работу, например, перемещая поршень, тем самым действуя, как тепловой двигатель.

Из каких процессов состоит Цикл Карно при работе в качестве теплового двигателя:

Изотермическое расширение. Тепло передаётся обратимо из высокотемпературного резервуара при постоянной температуре T H (изотермическое добавление или поглощение тепла). На этом этапе газу позволяют расширяться, выполняя работу над окружающей средой, толкая поршень. Хотя давление падает, температура газа не изменяется во время процесса, поскольку он находится в тепловом контакте с горячим резервуаром в момент времени T h и, следовательно, расширение является изотермическим.
Изоэнтропическое (обратимое адиабатическое) расширение газа. На этом этапе газ теплоизолирован как от горячего, так и от холодного резервуаров. Таким образом, они не получают и не теряют тепло. Газ продолжает расширяться за счёт снижения давления, выполнения работы на окружающую среду и потери количества внутренней энергии, равного проделанной работе. Расширение газа без подвода тепла приводит к его охлаждению до «холодной» температуры. Энтропия остаётся неизменной.
Изотермическая компрессия. Тепло передаётся обратимо в низкотемпературный резервуар при постоянной температуре (изотермический отвод тепла). Теперь газ в двигателе находится в тепловом контакте с холодным резервуаром. Окружение работает на газе, толкая поршень вниз, в результате чего количество тепловой энергии Q 2 покидает систему в низкотемпературный резервуар, а энтропия системы уменьшается.
Адиабатическое обратимое сжатие. Ещё раз газ в двигателе теплоизолирован от горячего и холодного резервуаров и предполагается, что двигатель не имеет трения и, следовательно, обратим. На этом этапе окружающая среда воздействует на газ, продвигая поршень вниз, увеличивая его внутреннюю энергию, сжимая и заставляя температуру подниматься обратно, но энтропия остаётся неизменной. В этот момент газ находится в том же состоянии, что и в начале шага 1.

Система, проходящая через этот цикл, называется тепловым двигателем Карно, хотя такой «идеальный» двигатель является лишь теоретической конструкцией и не может быть построен на практике. Тем не менее был разработан и запущен микроскопический тепловой двигатель.

По существу, есть два «тепловых резервуара», образующих часть теплового двигателя при температурах T h и T c (соответственно, горячий и холодный). Они обладают такой большой теплоёмкостью, что их температуры практически не зависят от одного цикла. Поскольку цикл теоретически обратим, энтропия в течение цикла не возникает, но сохраняется.

Во время цикла произвольное количество энтропии S извлекается из горячего резервуара (нагревателя) и осаждается в холодном резервуаре. Поскольку в обоих резервуарах изменения объёма не происходит, они не работают, и в течение цикла количество энергии T h ΔS извлекается из горячего резервуара, а меньшее количество энергии T c ΔS откладывается в холодном резервуаре. Разница в двух энергиях (T h -T c) ΔS равна работе, проделанной двигателем.

Поведение двигателя или холодильника Карно лучше всего понять с помощью диаграммы, в которой координатами являются температура и энтропия. Термодинамическое состояние определяется точкой на графике с энтропией (S) в качестве горизонтальной оси и температуры (T) в качестве вертикальной оси. Для простой замкнутой системы любая точка на графике будет представлять конкретное состояние системы. Термодинамический процесс будет состоять из кривой, соединяющей начальное состояние (A) и конечное состояние (B), и представляющей собой количество тепловой энергии, передаваемой в процессе.

Если процесс движется к большей энтропии, площадь под кривой будет количеством тепла, поглощённого системой. Когда процесс движется к меньшей энтропии, это будет количество отводимого тепла. Для любого циклического процесса есть верхняя часть цикла и нижняя часть. Для цикла по часовой стрелке область под верхней частью будет тепловой энергией, поглощённой в течение цикла, тогда как область под нижней частью будет тепловой энергией, удалённой во время цикла.

Площадь внутри цикла будет тогда разницей между ними, но поскольку внутренняя энергия системы должна вернуться к своему первоначальному значению, эта разница должна быть объёмом работы, которую должна совершать системой за цикл.

Перевёрнутый цикл

Описанный цикл теплового двигателя является полностью обратным циклом Карно. То есть все процессы, из которых он состоит, могут быть обращены вспять, и в этом случае цикл становится холодильным циклом Карно.

На этот раз цикл остаётся точно таким же, за исключением того, что направления любых тепловых и рабочих взаимодействий меняются местами. Тепло поглощается из низкотемпературного резервуара, отбрасывается в высокотемпературный резервуар, и для этого требуется работа. Диаграмма P-V обращённого цикла такая же, как и для цикла Карно, за исключением того, что направления процессов меняются местами.

Если же в цикле возникает передача теплоты при наличии разности температур, а такими являются все технические реализации термодинамических циклов, то цикл становится необратимым. КПД такого цикла будет всегда меньше, чем КПД цикла Карно.

Теорема Карно

Эта теорема является формальным утверждением этого факта: ни один двигатель, работающий между двумя тепловыми резервуарами, не может быть более эффективным, чем двигатель Карно, работающий между этими же резервуарами.

Следствие из теоремы Карно гласит: все реверсивные двигатели, работающие между одними и теми же тепловыми резервуарами, одинаково эффективны. Теоретический максимальный КПД теплового двигателя равён разнице в температуре между горячим и холодным резервуаром, делённой на абсолютную температуру горячего резервуара.

Исходя из этого, становится очевидным интересный факт: понижение температуры холодного резервуара будет иметь большее влияние на потолочную эффективность теплового двигателя, чем повышение температуры горячего резервуара на ту же величину. В реальном мире это труднодостижимо, так как холодный резервуар часто имеет существующую температуру окружающей среды.

Другими словами, максимальная эффективность достигается тогда, когда в цикле не создаётся новая энтропия, что было бы в случае, если, например, трение привело к рассеиванию работы в тепло. В противном случае, поскольку энтропия является функцией состояния, требуемый сброс тепла в окружающую среду для удаления избыточной энтропии приводит к (минимальному) снижению эффективности.

В мезоскопических тепловых двигателях работа за цикл обычно колеблется из-за теплового шума. Если цикл выполняется квазистатически, флуктуации исчезают даже на мезомасштабах. Но если цикл выполняется быстрее, чем время релаксации рабочего тела, колебания работы неизбежны. Тем не менее когда учтены рабочие и тепловые колебания, существует точное равенство, которое связывает экспоненциальное среднее значение работы, выполненной любым тепловым двигателем, и теплопередачу от горячей тепловой ёмкости.

Карно понимал, что в действительности невозможно создать термодинамический обратимый двигатель, поэтому реальные тепловые двигатели менее эффективны. Кроме того, реальные двигатели, работающие в этом цикле, встречаются редко. Но хотя прямой цикл французского учёного является идеализацией, его выражение эффективности всё ещё полезно для дальнейших исследований.

Примером обратимого цикла также является идеальный цикл Стирлинга. Существует и другие идеальные циклы, в которых коэффициент полезного действия определяется по той же формуле, что и для циклов Карно и Стирлинга, например, цикл Эрикссона.

Источник