Что такое полная работа и полезная

Физика — это наука, которая изучает процессы, происходящие в природе. Наука эта очень интересная и любопытная, ведь каждому из нас хочется удовлетворить себя ментально, получив знания и понимание того, как и что в нашем мире устроено. Физика, законы которой выводились не одно столетие и не одним десятком ученных, помогает нам с этой задачей, и мы должны только радоваться и поглощать предоставленные знания.
Но в то же время физика — наука далеко непростая, как, собственно, и сама природа, но разобраться в ней было бы очень интересно. Сегодня мы будем говорить о коэффициенте полезного действия. Мы узнаем, что такое КПД и зачем он нужен. Рассмотрим все наглядно и интересно.
Определение и расшифровка КПД
Расшифровка аббревиатуры — коэффициент полезного действия. Однако и такое толкование с первого раза может оказаться не особо понятным. Этим коэффициентом характеризуется эффективность системы или какого-либо отдельного тела, а чаще — механизма. Эффективность характеризуется отдачей или преобразованием энергии.
Этот коэффициент применим практически ко всему, что нас окружает, и даже к нам самим, причём в большей степени. Ведь совершаем мы полезную работу все время, только вот как часто и насколько это важно, уже другой вопрос, с ним и используется термин «КПД».
Важно учесть, что этот коэффициент — величина неограниченная, она, как правило, представляет собой либо математические значения, к примеру, 0 и 1, либо же, как это чаще бывает — в процентах.
В физике этот коэффициент обозначается буквой Ƞ, или, как её привыкли называть, Эта.

Полезная работа
При использовании каких-либо механизмов или устройств мы обязательно совершаем работу. Она, как правило, всегда больше той, что необходима нам для выполнения поставленной задачи. Исходя из этих фактов различается два типа работы: это затраченная, которая обозначается большой буквой, А с маленькой з (Аз), и полезная — А с буквой п (Ап). Для примера, возьмем такой случай: у нас есть задача поднять булыжник определенной массой на определенную высоту. В этом случае работа характеризует только преодоление силы тяжести, которая, в свою очередь, действует на груз.
В случае когда для подъема применяется какое-либо устройство, кроме силы тяжести булыжника, важно учесть еще и силу тяжести частей этого устройства. И кроме всего этого, важно помнить, что, выигрывая в силе, мы всегда будем проигрывать в пути. Все эти факты приводят к одному выводу, что затрачиваемая работа в любом варианте окажется больше полезной, Аз > Ап, вопрос как раз заключается в том, насколько её больше, ведь можно максимально сократить эту разницу и тем самым увеличить КПД, наш или нашего устройства.
Полезная работа — это часть затрачиваемой, которую мы совершаем, используя механизм. А КПД — это как раз та физическая величина, которая показывает, какую часть составляет полезная работа от всей затраченной.
Итог:
- Затрачиваемая работа Aз всегда больше полезной Ап.
- Чем больше отношение полезной к затрачиваемой, тем выше коэффициент, и наоборот.
- Ап находится произведением массы на ускорение свободного падения и на высоту подъема.

Физическая формула КПД
Существует определенная формула для нахождения КПД. Она звучит следующим образом: чтобы найти КПД в физике, нужно количество энергии разделить на проделанную системой работу. То есть КПД — это отношение затраченной энергии к выполненной работе. Отсюда можно сделать простой вывод, что тем лучше и эффективнее система или тело, чем меньше энергии затрачивается на выполнение работы.
Сама формула выглядит кратко и очень просто Ƞ будет равняться A/Q. То есть Ƞ = A/Q. В этой краткой формулы и фиксируют нужные нам элементы для вычисления. То есть A в этом случае является использованной энергией, которая потребляется системой во время работы, а большая буква Q, в свою очередь, будет являться затраченной A, или опять же затраченной энергией.
В идеале КПД равен единице. Но, как это обычно бывает, он её меньше. Так происходит по причине физики и по причине, конечно же, закона о сохранении энергии.
Все дело в том, что закон сохранения энергии предполагает, что не может быть получено больше А, чем получено энергии. И даже единице этот коэффициент будет равняться крайне редко, поскольку энергия тратится всегда. И работа сопровождается потерями: к примеру, у двигателя потеря заключается в его обильном нагреве.
Итак, формула КПД:
Ƞ=А/Q, где
- A — полезная работа, которую выполняет система.
- Q — энергия, которую потребляет система.
Применение в разных сферах физики
Примечательно, что КПД не существует как понятие нейтральное, для каждого процесса есть свой КПД, это не сила трения, он не может существовать сам по себе.
Рассмотрим несколько из примеров процессов с наличием КПД.
К примеру, возьмем электрический двигатель. Задача электрического двигателя — преобразовывать электрическую энергию в механическую. В этом случае коэффициентом будет являться эффективность двигателя в отношении преобразования электроэнергии в энергию механическую. Для этого случая также существует формула, и выглядит она следующим образом: Ƞ=P2/P1. Здесь P1 — это мощность в общем варианте, а P2 — полезная мощность, которую вырабатывает сам двигатель.
Нетрудно догадаться что структура формулы коэффициента всегда сохраняется, меняются в ней лишь данные, которые нужно подставить. Они зависят от конкретного случая, если это двигатель, как в случае выше, то необходимо оперировать затрачиваемой мощностью, если работа, то исходная формула будет другая.

Теперь мы знаем определение КПД и имеем представление об этом физическом понятии, а также об отдельных его элементах и нюансах. Физика — это одна из самых масштабных наук, но её можно разобрать на маленькие кусочки, чтобы понять. Сегодня мы исследовали один из этих кусочков.
Видео
Это видео поможет вам понять, что такое КПД.
Источник
Механическая работа – это одна из основных скалярных величин в физике. В рамках стандартной школьной программы она изучается в седьмом классе в разделе механики. Механическая работа – один из способов изменения внутренней энергии тела или субстанции (например, газа или жидкости) наряду с такими формами теплопередачи, как теплопроводность, конвекция и излучение, которые изучаются в разделе тепловых явлений.
Что такое работа в физике – определение и формула
Механическая работа – это количество энергии, которое нужно затратить для того, чтобы тело начало равномерно замедляющееся движение и прошло некоторую дистанцию.
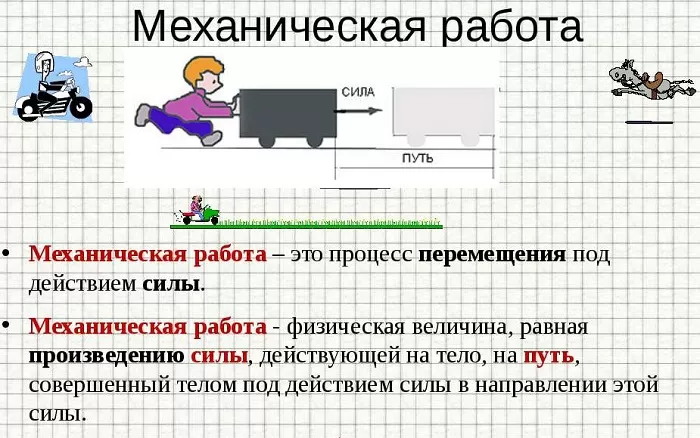
В физике механической работой называется произведение силы, которая действует на некоторое тело, на расстояние, которое оно проходит под ее воздействием:
A = F * S
В более сложных случаях в формуле появляется и третья величина – косинус угла, под которым друг к другу расположены векторы движения и приложенной силы. Найти ее значение можно по формуле:
A = F * S * cosA
В чем измеряется работа
Физические единицы, в которых выражается механическая работа, – Джоули.

Существуют разные способы для ее практического измерения, которые зависят от типа произведенного движения. При этом в формулу работы подставляют значение силы в Ньютонах и расстояния в метрах. Угол между векторами измеряют в математических единицах – градусах.
Работа силы трения
При условиях, существующих на Земле, на любое движущееся тело оказывает воздействие сила трения, замедляющая его движение. Чаще всего это трение поверхности, по которой движется объект. Это очевидно из того факта, что при воздействии постоянной силы на тело его скорость окажется переменной.
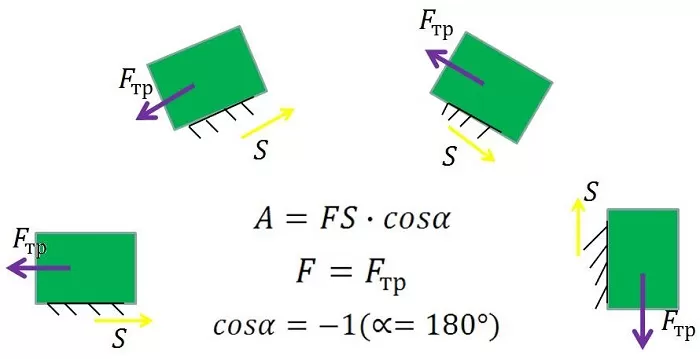
Следовательно, должна быть и другая сила, противодействующая ей – и это сила трения. Если система координат выбрана по направлению движения тела, то ее числовое значение будет отрицательным.
Положительная и отрицательная работа
Числовое значение работы, которую совершает сила, может становиться отрицательным в случае если ее вектор противоположен вектору скорости.
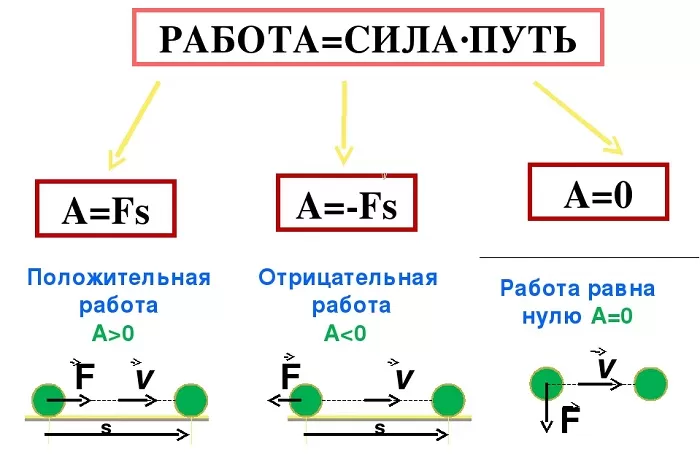
Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае она будет называться противодействующей.
Полезная или затраченная работа
У тела, совершающего одно и то же действие, есть два значения работы. Первая из них, полезная, вычисляется по обычной формуле.
Вторая, затраченная, по своему понятию не имеет общей формулы для вычисления и измеряется практически. Эта разница между совершенной в реальности работой и той, которая должна была быть совершена в теории, равна коэффициенту полезного действия – КПД. Он вычисляется так:
КПД = А полезная / А затраченная,
и выражается в процентах. КПД всегда меньше 100.

Мощность
Среднее количество работы, совершаемой за единицу времени (секунду), характеризует такую величину, как мощность. Формула для ее вычисления выглядит так:
Р = A / t
В качестве работы можно подставить люблю известную формулу для ее вычисления в зависимости от ситуации. Ответ будет выражен в Ваттах.
Однако при равномерном движении можно использовать и другую формулу:
Р = F * v
Подставив вместо обычной скорости мгновенную, можно получить значение мгновенной мощности.
Примеры решения задач
Рассмотрим несколько простых задач на нахождение механической работы.

Задача 1
Какую работу совершает подъемный механизм, поднимающий десятикилограммовый блок на высоту 50 метров.
Решение:
Для того, чтобы поднять тело, необходимо преодолеть действующую на него силу тяжести. То есть F, с которой поднимают блок, равна той, с которой он притягивается к земле. Так как последняя равна m * g, то для нахождения конечного результата понадобится только одна измененная версия стандартной формулы, упомянутой выше: A = S * m * g.
При помощи простой математики найдем числовой ответ:
A = 50 м * 10 кг * 10 Н/кг;
A = 5000 Дж.
Ответ: 5000 Дж.
Впрочем, не всегда речь идет о силе тяжести.
Задача 2
Какая работа совершается силой упругости, когда пружина с жесткостью 10 Н/м, сжатая на 20 см, возвращается в исходное состояние? Система замкнута, нет никаких внешних сил, воздействующих на пружину.
Решение:
Для начала нужно найти саму F упругости, которая совершает работу. Ее формула – F = x * |k|, где x – это длина, на которую сжимается или растягивается пружина, а k – коэффициент ее жесткости. Перемещение пружины равно ее деформации, и следовательно, конечная формула в этом случае будет выглядеть так: A = S * x * k = x * x * k = x^2 * k.
Далее при помощи элементарных вычислений рассчитаем ответ:
A = (0,2 м)^2 * 10 Н/м = 0,04 * 10 = 0,4 Дж.
Ответ: 0,4 Дж.
Но во всех задачах по данной теме траектория движения тела прямая.
Задача 3
Рассчитайте, какова сила, действующая на колесо, если на то, чтобы совершить полный оборот, ему требуется 10 кДж. Диаметр диска равен 40 см, а толщина шины – 10 см.
Решение:
В этом случае нам нужно найти не А, а F, но сделать это можно при помощи все той же формулы. Возьмем точку на поверхности колеса. Предположим, что при вращательном движении ее вектор будет противоположен вектору приложения силы, а значит косинусом в формуле вновь можно пренебречь. Таким образом, за один оборот колеса точка пройдет расстояние, равное длине окружности, которую можно вычислить как 2πr или πd. Диаметр окружности можно найти из предоставленных данных: он равен сумме диаметра диска и удвоенной толщины шины, то есть 40 см + 2 * 10 см = 40 см + 20 см = 60 см = 0,6 м.
Теперь, когда мы можем вычислить расстояние, у нас есть все данные для того, чтобы приступить к нахождению силы.
Формула работы для этого случая будет такой: A = F * π * d, то силу, соответственно, можно будет выразить как F = A / (π * d).
В таком случае:
F = 10 кДж / (3,14 * 0,6 м) = 10000 Дж / 1,884 м = ~ 5308 Н.
Ответ: 5308 Н.
В завершение решим самый сложный вариант задачи, включающий в себя все, о чем говорилось выше.
Задача 4
Автомобиль Фольксваген весом 2500 кг заезжает на гору. Какова должна быть его минимальная скорость, чтобы удержаться на горе, если сила тяги равна 10 кН, время работы двигателя – 10 с, КПД – 30%, а угол наклона горы – 60 градусов. Трением и прочими силами пренебречь.
Решение:
На первый взгляд задача может показаться сложной, но для ее решения используются только простые известные формулы.
Запишем условие в более наглядном виде.
Дано:
m = 2500 кг;
F = 10000 H;
t = 10 с;
КПД = 30%;
угол A = 1500 (60+90, т. к. сила тяжести приложена под углом 90 к горизонтали);
V – ?
Выведение формулы:
Шаг 1. По условию A1 (силы тяжести) = А2 (тяги).
A1 = mg;
A2 = P * t / КПД.
То есть mg = P * t / КПД.
Шаг 2. P = F * V * cosA.
Шаг 3. Общая формула: mg = F * V * cosA * t / КПД.
V = (m * g * КПД) / (F * t * cosA).
Числовое решение:
V = (2500 кг * 10 Н/кг * 30%) / (10000 H * 10 с * cos150);
V = (2500 кг * 10 Н/кг * 0,3) / (10000 H * 10 с * cos60);
V = 7500 / 50000;
V = 0,15 м/с.
Ответ: 0,15 м/с.
Источник
| ««« [ ] »»» | ||
| § 05-б. Коэффициент полезного действия | ||
Допустим, мы отдыхаем на даче, и нам нужно принести из колодца воды. Мы опускаем в него ведро, зачерпываем воду и начинаем поднимать. Не забыли, какова наша цель? Правильно: набрать воды. Но взгляните: мы поднимаем не только воду, но и само ведро, а также тяжёлую цепь, на которой оно висит. Это символизирует двухцветная стрелка: вес поднимаемого нами груза складывается из веса воды и веса ведра и цепи.
Рассматривая ситуацию качественно, мы скажем: наряду с полезной работой по подъёму воды мы совершаем и другую работу – подъём ведра и цепи. Разумеется, без цепи и ведра мы не смогли бы набрать воды, однако, с точки зрения конечной цели, их вес «вредит» нам. Если бы этот вес был бы меньше, то и полная совершённая работа тоже была бы меньше (при той же полезной). Теперь перейдём к количественному изучению этих работ и введём физическую величину, называемую коэффициентом полезного действия. Задача. Яблоки, отобранные для переработки, грузчик высыпает из корзин в грузовик. Масса пустой корзины 2 кг, а яблок в ней – 18 кг. Чему равна доля полезной работы грузчика от его полной работы? Решение. Полной работой является перемещение яблок в корзинах. Эта работа складывается из подъёма яблок и подъёма корзин. Важно: поднятие яблок – полезная работа, а поднятие корзин – «бесполезная», потому что цель работы грузчика – переместить только яблоки.
| ||
Введём обозначения: Fя – сила, с которой руки поднимают вверх только яблоки, а Fк – сила, с которой руки поднимают вверх только корзину. Каждая из этих сил равна соответствующей силе тяжести: F=mg. Пользуясь формулой A = ±( F||· l ) , «распишем» работы этих двух сил: Aполезн = +Fя · lя = mяg · h и Aбесполезн = +Fк · lк = mкg · h Полная работа складывается из двух работ, то есть равна их сумме: Aполн = Aполезн + Aбесполезн = mяg h + mкg h = ( mя + mк ) · g h В задаче нас просят вычислить долю полезной работы грузчика от его полной работы. Сделаем это, поделив полезную работу на полную:
В физике такие доли принято выражать в процентах и обозначать греческой буквой «η» (читается: «эта»). В итоге получим: η = 0,9 или η = 0,9 ·100% = 90% , что то же самое. Это число показывает, что из 100% полной работы грузчика доля его полезной работы составляет 90%. Задача решена. Физическая величина, равная отношению полезной работы к полной совершённой работе, в физике имеет собственное название – КПД – коэффициент полезного действия:
После вычисления КПД по этой формуле его принято умножать на 100%. И наоборот: для подстановки КПД в эту формулу его значение нужно перевести из процентов в десятичную дробь, поделив на 100%.
| ||||||||||||||||||||||||
Источник
Определение 1
КПД (коэффициент полезного действия) – величина, характеризующая
соотношение используемой энергии к затрачиваемой, т.е. энергетическую эффективность системы.
КПД измеряется в процентах или указывается как десятичная дробь от 0 до 1. КПД 50% (или, что тоже самое– 0,5) означает, что только половина энергии используется для выполнения работы. Остальная рассеивается в окружающем пространстве, как правило, в форме тепла.
Замечание 1
Коэффициент полезного действия паровозов, применявшихся для железнодорожных перевозок в XIX – первой половине XX вв., составлял менее 10%, т.е. 90 и более процентов тепла от сжигаемого в топках угля улетучивалось в атмосферу, не выполняя полезной работы по вращению колес, приводящему к движению состав. Для сравнения: КПД пришедших на смену паровозам тепловозов (в них используются не паровые, а дизельные двигатели) достигает 40%.
КПД в формулах обозначают греческой буквой $eta$ (эта).
$eta = frac{A_п}{A_з}$
, где $A_п$ – полезная работа, $A_з$ – затраченная.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Полезная работа и потери энергии
“Полезность” выполняемой работы – величина субъективная, связанная с человеческим восприятием, поэтому о КПД говорят чаще всего применительно к искусственно созданным системам. Несмотря на то, что технологии совершенствуются, избежать потерь в рукотворных системах инженерам не удастся:
- в механических устройствах часть затрачиваемой энергии всегда тратится на преодоление сил трения между соприкасающимися деталями (эти силы уменьшают за счет более тщательной обработки и смазки);
- в электрических системах часть энергии рассеивается в виде тепла при преодолении сопротивления проводников (явление сверхпроводимости еще не применимо к практике и требует низких температур);
- в нагревательных приборах утечки происходят в силу дефектов теплоизоляции и т.п.
Таким образом,
$A_з$ > $A_п$
, где $A_з$ – работа затраченная, $A_п$ – работа полезная.
Потери энергии можно сводить к минимуму, но полностью исключить их невозможно. Какое бы совершенное устройство мы не придумали, КПД никогда не достигнет единицы в силу второго закона термодинамики, действие которого исключает создание механизмов с КПД равным или большим 100%.
КПД различных физических процессов
Методики подсчета КПД разнятся в зависимости от физической природы явлений, задействованных в преобразующих энергию системах.
При практических расчетах, связанных с движением, знаменатель формулы КПД удобнее представить не как работу (произведение силы на расстояние), а как затраченную энергию, выделившуюся, например, при сжигании топлива:
$eta = frac{A_п}{Q}$
, где $A_п$ — выполненная системой полезная работа, $Q$ — затраченная системой энергия.
Например, зная сколько бензина истрачено двигателем автомобиля (количество выделившегося в результате тепла можно легко подсчитать), а также массу, скорость и пройденное расстояние, легко найти КПД.
Если речь идет не об автомобиле с двигателем внутреннего сгорания, а об электромобиле, то затраты энергии в знаменателе можно подсчитать как произведение средних тока и напряжения за время движения рассматриваемого транспортного средства.
Поскольку мощность представляет собой работу, выполняемую в единицу времени, КПД иногда бывает удобно посчитать как соотношение входной и выходной мощностей системы:
$eta = frac{P_{out}}{P_{in}}$
, где $P_{in}$ – мощность на входе системы, $P_{out}$ – на выходе.
Такой подход удобен, например, при расчете КПД солнечных батарей. В знаменателе в этом случае будет мощность светового излучения, падающего на их поверхность, в числителе – мощность генерируемого тока.
Пример 1
Лебедка, потребляющая мощностью 500 Вт, за время 10 с подняла груз массой 70 кг на высоту 5м. Найти КПД лебедки.
Лебедка преодолела силу тяжести, совершив работу
$A_л = m cdot g cdot h$
, где $m$ – масса, $g$ – ускорение свободного падения, $h$ высота.
Подставив значения, получаем:
$A = 70 cdot 9,8 cdot 5 = 3430 Дж$
Затраченную энергию найдем через мощность и время:
$Q = P cdot t$
, где $Q$ – энергия, $P$ – мощность, $t$ – время.
Подставив значения, получаем:
$Q = 500 Вт cdot 10 с = 5000 Дж$
КПД находим как соотношение
$eta = frac{A}{Q} = frac{3430}{5000}cdot 100$% = $68,6$%
Ответ: КПД лебедки равен 68,6%.
Источник
