Чему равна полезная работа совершенная газом за цикл
В программу школьного курса физики входит ряд вопросов, связанных с тепловыми двигателями. Школьник должен знать основные принципы работы теплового двигателя, понимать определение коэффициента полезного действия (КПД) циклического процесса, уметь находить эту величину в простейших случаях, знать, что такое цикл Карно и его КПД.
Тепловым двигателем (или тепловой машиной) называется процесс, в результате которого внутренняя энергия какого-то тела превращается в механическую работу. Тело, внутренняя энергия которого превращается двигателем в работу, называется нагревателем двигателя. Механическая работа в тепловых машинах совершается газом, который принято называть рабочим телом (или рабочим веществом) тепловой машины. При расширении рабочее тело и совершает полезную работу.
Для того чтобы сделать процесс работы двигателя циклическим, необходимо еще одно тело, температура которого меньше температуры нагревателя и которое называется холодильником двигателя. Действительно, если при расширении газ совершает положительную (полезную) работу (левый рисунок; работа газа численно равна площади «залитой» фигуры), то при сжатии газа он совершает отрицательную («вредную») работу, которая должна быть по абсолютной величине меньше полезной работы. А для этого сжатие газа необходимо проводить при меньших температурах, чем расширение, и, следовательно, газ перед сжатием необходимо охладить. На среднем рисунком показан процесс сжатия газа 2-1, в котором газ совершает отрицательную работу , абсолютная величина которой показана на среднем рисунке более светлой «заливкой». Чтобы суммарная работа газа за цикл была положительна, площадь под графиком расширения должна быть больше площади под графиком сжатия. А для этого газ перед сжатием следует охладить. Кроме того, из проведенных рассуждений следует, что работа газа за цикл численно равна площади цикла на графике
|
зависимости давления от объема, причем со знаком «плюс», если цикл проходится по часовой стрелке, и «минус» — если против.
Таким образом, двигатель превращает в механическую работу не всю энергию, взятую у нагревателя, а только ее часть; остальная часть этой энергии используется не для совершения работы, а передается холодильнику, т.е. фактически теряется для совершения работы. Поэтому величиной, характеризующей эффективность работы двигателя, является отношение
| (15.1) |
где — работа, совершаемая газом в течение цикла, — количество теплоты, полученное газом от нагревателя за цикл. Отношение (15.1) показывает, какую часть количества теплоты, полученного у нагревателя, двигатель превращает в работу и называется коэффициентом полезного действия (КПД) двигателя.
Если в течение цикла рабочее тело двигателя отдает холодильнику количество теплоты (эта величина по своему смыслу положительна), то для работы газа справедливо соотношение . Поэтому существует ряд других форм записи формулы (15.1) для КПД двигателя
| (15.2) |
Французский физик и инженер С. Карно доказал, что максимальным КПД среди всех процессов, использующих некоторое тело с температурой в качестве нагревателя, и некоторое другое тело с температурой ( ) в качестве холодильника, обладает процесс, состоящий из двух изотерм (при температурах нагревателя и холодильника ) и двух адиабат (см. рисунок).
|
Изотермам на графике отвечают участки графика 1-2 (при температуре нагревателя ) и 3-4 (при температуре холодильника ), адиабатам — участки графика 2-3 и 4-1. Этот процесс называется циклом Карно. КПД цикла Карно равен
| (15.3) |
Теперь рассмотрим задачи. В задаче 15.1.1 необходимо использовать то обстоятельство, что работа газа в циклическом процессе численно равна площади цикла на графике зависимости давления от объема, причем со знаком «плюс», если цикл проходится по часовой стрелке, и «минус» — если против. Поэтому во втором цикле работа газа положительна, в третьем отрицательна. Первый цикл состоит из двух циклов, один из которых проходится по, второй — против часовой стрелки, причем, как следует из графика 1, площади этих циклов равны. Поэтому работа газа за цикл в процессе 1 равна нулю (правильный ответ — 2).
Поскольку в результате совершения циклического процесса газ возвращается в первоначальное состояние (задача 15.1.2), то изменение внутренней энергии газа в этом процессе равно нулю (ответ 2).
Применяя в задаче 15.1.3 первый закон термодинамики ко всему циклическому процессу и учитывая, что изменение внутренней энергии газа равно нулю (см. предыдущую задачу), заключаем, что (ответ 3).
Поскольку работа газа численно равна площади цикла на диаграмме «давление-объем», то работа газа в процессе в задаче 15.1.4 равна (ответ 1). Аналогично в задаче 15.1.5 газ за цикл совершает работу (ответ 1).
Работа газа в любом процессе равна сумме работ на отдельных участках процесса. Поскольку процесс 2-3 в задаче 15.1.6 — изохорический, то работа газа в этом процессе равна нулю. Поэтому (ответ 3).
По определению КПД показывает, какую часть количества теплоты, полученного у нагревателя, двигатель превращает в работу (задача 15.1.7 — ответ 4).
Работа двигателя за цикл равна разности количеств теплоты, полученного от нагревателя и отданного холодильнику : . Поэтому КПД цикла есть
|
(задача 15.1.8 — ответ 3).
По формуле (15.3) находим КПД цикла Карно в задаче 15.1.9
|
(ответ 2).
Пусть температура нагревателя первоначального цикла Карно равна , температура холодильника (задача 15.1.10). Тогда по формуле (15.3) для КПД первоначального цикла имеем
|
Отсюда находим . Поэтому для КПД нового цикла Карно получаем
|
(ответ 2).
В задаче 15.2.1 формулы (2), (3) и (4) представляют собой разные варианты записи определения КПД теплового двигателя (см. формулы (15.1) и (15.2)). Поэтому не определяет КПД двигателя только формула 1. (ответ 1).
Мощностью двигателя называется работа, совершенная двигателем в единицу времени. Поскольку работа двигателя равна разности полученного от нагревателя и отданного холодильнику количеств теплоты, имеем для мощности двигателя в задаче 15.2.2
|
(ответ 3).
По формуле (15.2) имеем для КПД двигателя в задаче 15.2.3
|
где — количество теплоты, полученное от нагревателя, — количество теплоты, отданное холодильнику (правильный ответ — 2).
Для нахождения КПД теплового двигателя в задаче 15.2.4 удобно использовать последнюю из формул (15.2). Имеем
|
где — работа газа, — количество теплоты, отданное холодильнику. Поэтому правильный ответ в задаче — 3.
Пусть газ совершает за цикл работу (задача 15.2.5). Поскольку количество теплоты, полученное от нагревателя равно ( — количество теплоты, отданное холодильнику), и работа составляет 20 % от этой величины, то для работы справедливо соотношение = 0,2 ( + 100). Отсюда находим = 25 Дж (ответ 1).
Поскольку работа теплового двигателя в задаче 15.2.6 равна 100 Дж при КПД двигателя 25 %, то двигатель получает от нагревателя количество теплоты 400 Дж. Поэтому он отдает холодильнику 300 Дж теплоты в течение цикла (ответ 4).
Цикл, данный в задаче 15.2.8, состоит из двух изотерм 2-3 и 4-1 и двух изохор 1-2 и 3-4. Работа газа в изохорических процессах равна нулю. Сравним работы газа в изотермических процессах. Для этого удобно построить график зависимости давления от объема в рассматриваемом процессе, поскольку работа газа есть площадь под этим графиком. График зависимости давления от объема для заданного в условии процесса приведен на рисунке. Поскольку изотерме 2-3 соответствует бóльшая температура, чем изотерме 4-1, то она будет расположена выше на графике . Объем газа в процессе 2-3 увеличивается, в процессе 4-1 уменьшается. Таким образом, график процесса на графике проходится по часовой стрелке, и, следовательно, работа газа за цикл положительна (ответ 1).
Для сравнения работ газа на различных участках процесса в задаче 15.2.9 построим график зависимости давления от объема. Этот график представлен на рисунке. Из рисунка следует, что работы газа в процессах 1-2 и 3-4 одинаковы по модулю (этим работам отвечают площади прямоугольников, «залитых» на рисунке светлой и темной «заливкой»). Работе газа на участке 4-1 отвечает площадь под графиком 4-1, которая меньше площади под графиком 1-2. Работе газа на участке 2-3 отвечает площадь под кривой 2-3 на рисунке, которая заведомо больше площади «залитых» прямоугольников. Поэтому в процессе 2-3 газ и совершает наибольшую по абсолютной величине (среди рассматриваемых процессов) работу (ответ 2.).
Согласно определению коэффициент полезного действия представляет отношение работы газа за цикл к количеству теплоты , полученному от нагревателя . Как следует из данного в условии задачи 15.2.10 графика, и в процессе 1-2-4-1 и в процессе 1-2-3-1 газ получает теплоту только на участке 1-2. Поэтому количество теплоты, полученное газом от нагревателя в процессах
1-2-4-1 и 1-2-3-1 одинаково. А вот работа газа в процессе 1-2-4-1 вдвое меньше (так площадь треугольника 1-2-4 как вдвое меньше площади треугольника 1-2-4-1). Поэтому коэффициент полезного действия процесса 1-2-4-1 вдвое меньше коэффициента полезного действия процесса 1-2-3-1 (ответ 1).
Источник
ТЕМА: “РЕШЕНИЕ ЗАДАЧ НА РАССЧЕТ РАБОТЫ В
ТЕРМОДИНАМИКЕ МЕТОДОМ ДИАГРАММ СОСТОЯНИЙ”.
Тип урока: урок закрепления изучаемого
материала.
Задачи урока.
Для ученика | Для учителя. |
Обучающие: | Обучающие: |
| а) осмыслить понятие “работа”; б) закрепить теоретические знания о в) научиться применять знания на | а) организовать процесс б) активизировать |
Развивающие: | Развивающие: |
а) развивать умение | а) развивать умение б) развивать умение обобщать и в) развивать умение разрешать |
Воспитывающие | Воспитывающие |
а) воспитывать б) воспитывать в себе “небоязнь” сложных | а) воспитывать умение б) воспитывать умение слушать, спорить; б) воспитывать умение интенсивно |
Оборудование. Дидактический материал.
1. Графопроектор, слайды.
2. Раздаточный материал.
3. Задачник. Л. А. Кирик. Физика-10.
Разноуровневые самостоятельные и контрольные
работы. М.: “Илекса”, 2004. – 192.: ил.
Ход урока
Введение.
Сегодня второй урок по теме: “ Работа в
термодинамике”. Усвоили ли Вы на первом уроке
физическую сущность работы в термодинамических
процессах? Решение задач сегодня это покажет. Наш
урок пройдёт в форме аукциона. Аукцион (“auctio”
(лат.) – продажа с публичных торгов) – способ
продажи, при котором товар предварительно
выставляют для осмотра. Я выставляю типы задач на
аукцион, объявляю количество баллов за каждый
тип. Вы предлагаете ответы, получаете за них
баллы, которые будут суммироваться
индивидуально у каждого из Вас. В конце урока
суммированные баллы определят Ваши отметки. За
урок можно получить одну и более отметок. (1
минута)
Основная часть. Аукцион задач.
1. Начнём с “аукциончика”
графиков (проецирую на экран слайд с графиками
через графопроектор).
(2 минуты).
Задача №1. На аукцион выставлены три
очень известных графические зависимости в осях
(p,V). (Рис. 1).
Какую информацию Вы можете извлечь из
этих диаграмм?
Отвечайте, пожалуйста, по одному.
Правильный ответ – 0,5 балла.
Рис. 1
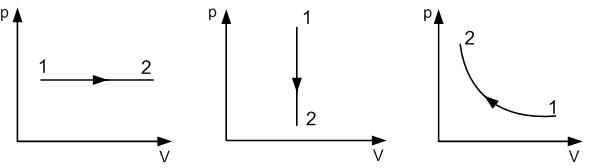
Ответы:
1. первый процесс – изобарное 2. второй процесс – изохорное 3. третий процесс – изотермическое 4. А1 = p (V2 –V1). | 5. А2 =0. 6. А3 = ? R T ln V2 /V1 7. А1 > 0. 8. А3 < 0. |
(Учащиеся отвечают устно с мест.)
Итоги “аукциончика”. (Объявляю баллы.)
2. От предварительного
“аукциончика” простейших графиков мы
продвигаемся к “аукциону простых задач”.
На аукцион выставлены на выбор задача
№ 5 (средний уровень) по цене 0,5 балла и задача
№ 1
(достаточный уровень) по цене 1 балл
на стр. 39 задачника.
Решения этих задачи потребуются в
дальнейшем при рассмотрении более сложных задач.
Время решения 2 минуты.
Задача №2.
Вариант А на 0,5 балла.
На рисунке 2 показана изобара газа в
координатах р, V. Определите работу,
совершенную газом в процессе расширения.
Рис. 2
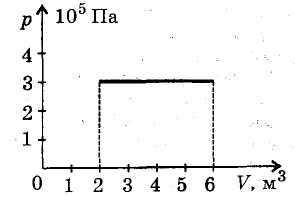
Решение.
А = p (V2 –V1).
А = 1,2 МДж.
Вариант Б на 1 балл.
Азот массой 280 г был нагрет при постоянном
давлении на 100 °С. Определить работу расширения
газа.
Решение.
А = p ?V; p ?V = m/µ R?T; А = m/µ R?T.
А = 8,31 кДж.
(Учащиеся выполняют задачи в тетрадях и,
получив ответ, поднимают руку. Учитель подходит к
ним проверяет и выставляет баллы за правильный
ответ. Два ученика в это время решают задачи на
обратной стороне доски. Через 2 мин открываем
решения на доске, проверяем его. Ученики у доски
получают баллы в случае правильного решения).
Итоги “аукциона простых задач”.
(Объявляю баллы.)
3. Теперь перейдём к “аукциону
задач”.
Итак, нахождение работы с помощью
графика зависимости р(V). За задачу можно
заработать 3 балла. Эта задача № 3 на карточке
лежащей, на парте.
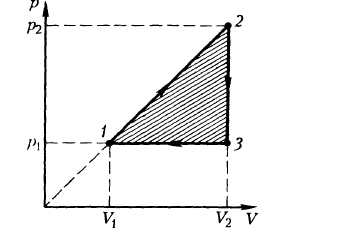
Задача №3. Газ расширился из
состояния с объемом V1 и давлением р1 в
состояние с объёмом V2 и давлением р2 в
процессе, при котором его давление зависит от
объёма линейно. Найти работу газа. Давление р1
меньше давления р2. . Время решения 2 мин.
Решение.
Построим график зависимости,
указанной в задаче, в координатах (р, V).
Рис. 3
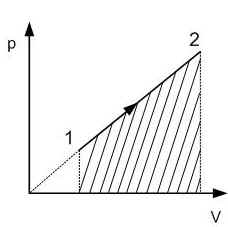
Работа газа численно равна площади
трапеции.
А= ? (p1+ p2) (V2 – V1).
(Учащиеся выполняют задачу в тетрадях
и, получив ответ, поднимают руку. Учитель
подходит, проверяет и выставляет 2 балла за
правильный ответ. Через фиксированное время
проецируется помощь (через 1 мин) и решение задачи
(через 2 мин) с помощью графопроектора. Один
ученик решает задачу на пленке графопроектора,
лампа которого выключены. Через 2 мин
проецируется решение, ученик делает пояснение).
Итоги “аукциона задач”. (Объявляю
баллы.)
4. На аукцион выставляется хорошая
задача на нахождение работы с помощью диаграммы
состояния в осях (р, V). Итак, “аукцион хороших
задач”. Эта задача № 4 на карточке лежащей,
на парте. (Приложение). Правильное
решение задачи оценивается в 5 баллов. В процессе
решения я буду проецировать на экран подсказки.
Сделавший всю задачу до подсказки, получит за неё
4 балла, после первой подсказки – 3 балла, после
второй – 2 балла, а затем открывается всё решение
задачи.
(В подсказках поэтапно открываю: 1.
изотерму; 2. формулу работы).
Задача № 4.
Идеальный газ переводят изотермически
из состояния 1 в состояние 2 (V2< V1),
затем изобарно в состояние 3, возвращают изохорно
в состояние 1. Начертите данный процесс в осях
(р,V). Покажите штриховкой площадь, численно
равную работе за цикл. Положительную или
отрицательную работу совершает газ за цикл?
Поясните. Время решения 3 мин.
Решение:
Рис. 4
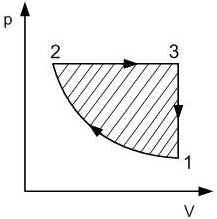
А = А12 + А23 + А31.
А12 < 0;
А23 > 0 Работа на участке 2 – 3
максимальна по модулю.
А31 =0.
Полная работа за цикл положительна.
(Учащиеся выполняют задачу в тетрадях
и, получив ответ, поднимают руку. Учитель
подходит, проверяет и выставляет 5 баллов за
правильное решение. Через отведенное время
проецируется решение задачи через
графопроектор. Решение на слайде пишет и
поясняет ученик, который сделал задачу первым).
Итоги “аукциона сложных задач”.
(Объявляю баллы).
5. На аукцион выставляется сложная
задача. Эта задача № 5 на карточке лежащей,
на парте. (Приложение). Ее правильное
решение оценивается в 5 баллов. Итак, “Аукцион
сложных задач”. Время выполнения задачи 5
минут.
Задача №5. С молем идеального одноатомного
газа совершен цикл, изображенный на рис. 5.
Температуры газа в различных состояниях равны Т1,
Т2, Т3, Т4. Найдите работу газа за
цикл.
Рис. 5
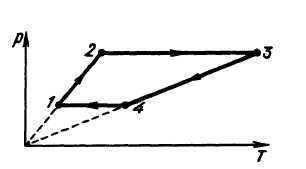
Подсказка-вопрос: А что Вы предполагаете
делать? (Ответ: Изобразить данный цикл в
координатах (p,V).)
Вопрос: Подумайте, а стоит ли?
Решение.
Из рис. 5 видно, что на участках 1 – 2 и 3 – 4
реализуется прямая пропорциональная
зависимость давления от температуры, т. е., как
следует из закона Менделеева — Клапейрона, объем
газа при этом не меняется, а значит, и работы газ
не совершает.
Необходимо найти работу газа лишь при
изобарических процессах 2 — 3 и 4 — 1.
На участке 2 — 3 совершенная работа будет равна
А23 = р2 (V3 – V2).
На участке 4 — 1 совершенная работа будет равна
А41 = р1 (V1 – V4).
Работа за цикл А = р2 (V3 – V2). + р1
(V1 – V4).
Уравнение Менделеева — Клапейрона
записывается в виде p V=? R T.
р1 V1 = v R T1 ; р1 V4
= v R T4 ; р2 V3 = v R T3 ;
р2 V2= v R T2.
Подставляя эти значения в выражение для работы,
получаем окончательно:
А = v R(T1 + T3 – T2 – T4).
(Решение проецируется через
графопроектор. Решение на слайде пишет и
поясняет ученик, сделавший задачу первым).
Итоги “аукциона сложных задач”.
(Объявляю баллы.)
6. Наконец, на аукцион выставляется
самая сложная на сегодняшний урок задача.
Начинаем “Аукцион конкурсных
задач”. Эта задача № 6 на карточке лежащей,
на парте. (Приложение). Правильное
решение задачи оценивается в 5 + 5 баллов. Время
решения 7 мин.
Тем, кого не устраивает эта задача,
предлагаю решить №1 (высокий уровень) стр. 40
задачника. Правильное решение – 5 баллов.
Задача № 6.
Вариант А на 5 баллов.
Один моль идеального газа совершает замкнутый
процесс, состоящий из двух изохор и двух изобар
(Рис. 6). Температура в точке1 равна T1, в точке
3 — T3. Определить работу, совершаемую газом
за цикл, если точки 2 и 4 лежат на одной изотерме.
Рис. 6
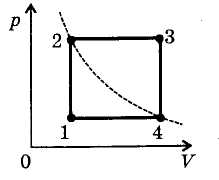
Решение.
На участках 1 —2 и 3 —4 работа равна
нулю.
Полная работа газа за цикл: А = А23
+ А41.
А23 = р2 (V3 – V2). Используя
уравнение Менделеева—Клапейрона, получим: р2
V3 = v R T3;
р2 V2= v R T2. Таким образом, А23
= v R T3 – v R T2.
Аналогично, А41 = v R T1 – v R T4.
Полная работа А = v R T3 – v R T2. +
v R T1 – v R T4. По условию T2
= T4.
А = v R T3. + v R T1 – 2v R T2.
Выразим T2. через T1 и T3.
Процесс 1—2 — изохорический, поэтому T1 / T2
= р1 / р2 .
В изобарическом процессе 2—3 T3 / T2 = V3
/ V2.
Умножив первое равенство на второе, получим:. T1
T3 / T 22 = р1 V3 / р2
V2 .
Учтем, что р1 = р4 и V3 = V4.
T1 T3 / T 22 = р4 V4 /
р2 V2;но р4 V4 = р2
V2; поэтому T1 T3 / T22 = 1.
T2 = v T1 T3 .
Работа за цикл А = v R (T3. + T1 – 2 v
T1 T3).
Окончательно получаем: А = v R (vT3. – v
T1)?.
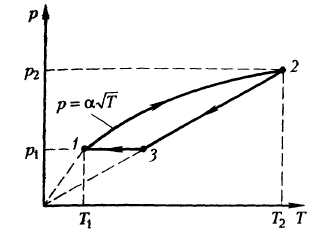
Вариант Б на 5 + 5 баллов.
Над одним молем идеального газа совершается
цикл, показанный графически на рисунке 7. Какую
работу совершает газ во время этого процесса?
Данные взять с рисунка.
Рис. 7
Подсказка-вопрос: А что Вы предполагаете
делать? (Ответ: Изобразить данный цикл в
координатах (p,V)).
Правильно.
Решение.
Нарисуем график зависимости в координатах (p,V).)
для данного процесса (рис. 8).
Рис. 8
На участке 1 —2 давление меняется по закону р = V, где — некоторая постоянная.
Выразим температуру газа через давление: Т = р2
/2 и
подставим в уравнение Менделеева—Клапейрона.
Получим р = 2
V/vR. Давление прямо пропорционально объему.
На этом участке газ совершает положительную
работу. Процесс 2—3 — изохорический, во время
этого процесса работа равна нулю. В
изобарическом процессе 3—1 работа совершалась
над газом, т. е. газ совершал отрицательную
работу. Полная работа газа равна площади
треугольника 1 2 3:
А = (р2 – р1) (V2–V1) /2.
Так как V2 = v R T2 / р2, V1 =
vRT1 / р1, окончательно получаем:
А = 0,5 v R (р2 – р1) (T2 / р2
– T1 / р1).
(Решение пишет на доске и поясняет
первый ученик, решивший задачу).
Итоги“Аукциона конкурсных
задач”. (Объявляю баллы.)
7. В заключение урока предлагаю “аукцион
олимпиадных задач”. Пятерка достанется только
одному ученику за идею и мгновенный ответ.
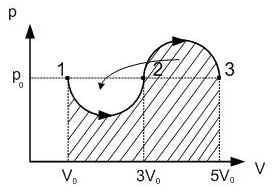
Задача №7.
Газ переводят из состояния 1 в состояние 3 в
процессе, изображенном на диаграмме в
координатах (p,V). (Проецирую на экран слайд через
графопроектор).
Линии 1 – 2 и 2 – 3 представляют собой
полуокружности равных диаметров. Найти работу
газа в данном процессе. Данные взять с диаграммы.
Рис. 9
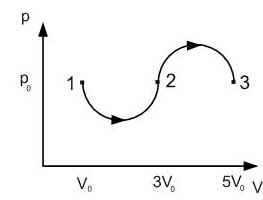
Решение.
Преобразуем графическую зависимость к виду:
| Рис. 10
| Рис. 11
|
Работа газа численно равна площади
прямоугольника:
А = р0 (5V0 – V0).
А = 4 р0V0.
(Решение проецируется через
графопроектор. Решение на слайде пишет и
поясняет первый ученик, решивший задачу).
Задание на дом. . Предлагается решить
достаточно сложную задачу №8. Её цена 5 + 5
баллов. Задача №8 помещена на стенде
кабинета.
Тем, кого не устраивает эта задача, предлагаю
решить № 31. 1 и 31. 4 на стр. 160 учебника под ред. А. А.
Пинского.
Задача №8. Найдите работу, совершенную молем
идеального газа в цикле, состоящем из двух
участков линейной зависимости давления от
объема и изохоры (рис. 12). Точки 2 и 3 лежат на
изотерме, прямая 3— 1 проходит через начало
координат. Заданы температуры Т1, и Т2,
Т3. .
Рис. 12
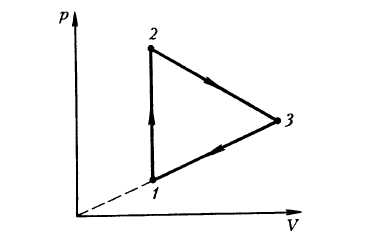
Решение:
Работа на изохоре 1 – 2 равна нулю. Работа на
участке 2 – 3 равна площади трапеции. Учтя, что
р 2V 2 = р 3V 3 = ?RT 2,
имеем:
Поскольку прямая 3 – 1 проходит через начало
координат и, следовательно, р1/V1 = р3/V3
получаем:
Т 1/V12 = Т 2/V22
= Т 3/V32 . Поэтому работу А 23
можно окончательно записать в виде:
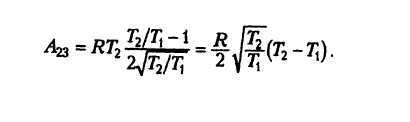
Работа на участке 3—1 тоже равна площади
трапеции:
Искомая работа в цикле равна:
Для участка прямой 2—3, соединяющего точки
изотермы, так же как и для самой изотермы, работа
газа определяется лишь отношением объемов.
Работа же газа вдоль участка произвольной
прямой, проходящей через начало координат на
диаграмме р V, определяется лишь разностью
температур конечного и начального состояний.
Заключение.
Сегодня было выставлено на интеллектуальный
аукцион немало задач, и вы с ними справились.
“Много задач вместе иногда решить легче, чем
одну из них, если то большее число задач хорошо
согласовано, а одна задача сама по себе
изолирована” (Д. Пойа). Не правда ли?
Окончательные итоги. Максимальное количество
решенных задач за урок –
Максимальная оценка за урок –
(Объявляю оценки. Некоторые учащиеся могут
получить за урок несколько оценок за интенсивную
умственную работу).
Надеюсь, все получили удовольствие от
интеллектуальной деятельности.
Литература.
1. Физика: Учеб. для 10 кл. шк. и кл. с углубл.
изучением физики / О. Ф. Кабардин, В. В. Орлов, Э. Е.
Эвенчик. ; под ред. А. А. Пинского. – 7-е изд. –М.:
Просещение, 2002. – 415 с.: ил.
2. Л. А. Кирик. Физика-10. Разноуровневые
самостоятельные и контрольные работы. М.:
“Илекса”, 2004. – 192 с.: ил.
3. Практикум абитуриента. Молекулярная
физика, оптика, квантовая физика. Под ред. В. В
Можаева и А. И. Черноацана. Приложение к журналу
“Квант” №2, 1995. – М.: – Бюро “Квантум”.
4. Ю. А. Конаржевский. Анализ урока. М.: – Центр
“педагогический поиск”, 2003. – 336с.
Источник