2 цикл карно коэффициент полезного действия цикла карно для идеального газа
Устройство, имеющее способность преобразовывать полученную теплоту в механическую работу носит название теплового двигателя. В таких машинах механическая работа совершается в процессе расширения вещества, называющегося рабочим телом. Его роль обычно исполняют газообразные вещества, вроде паров бензина, воздуха и водяного пара.
Определение 1
Рабочее тело приобретает или отдает тепловую энергию при теплообмене с телами, которые имеют внушительный запас внутренней энергии. Такие тела называют тепловыми резервуарами.
Исходя из первого закона термодинамики, можно сделать вывод, что полученное газом количество теплоты Q полностью преобразуется в работу A в условиях изотермического процесса, при котором внутренняя энергия не претерпевает изменений (ΔU=0):
A=Q
Однако, подобный однократный акт превращения теплоты в работу для техники не представляет интереса. Существующие тепловые двигатели, такие как паровые машины, двигатели внутреннего сгорания и им подобные, работают циклически. Необходимо периодическое повторение процесса теплопередачи и преобразования полученной теплоты в работу. Чтобы данное условие выполнялось, рабочее тело должно совершать круговой процесс или же термодинамический цикл, при котором исходное состояние с периодически восстанавливается. На рисунке 3.11.1 в виде диаграммы (p, V) газообразного рабочего тела с помощью замкнутых кривых проиллюстрированы круговые. В условиях расширения газ производит положительную работу A1, эквивалентную площади под кривой abc. При сжатии газ совершает отрицательную работу A2, равную по модулю площади под кривой cda. Полная работа за цикл A=A1+A2 на диаграмме (p, V) равняется площади цикла. Работа A положительна, в том случае, если цикл проходит по часовой стрелке, и A отрицательна, когда цикл проходит в противоположном направлении.
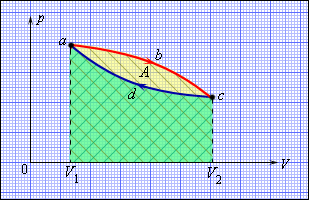
Рисунок 3.11.1. Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе равна площади фигуры abcd.
Все круговые процессы обладают общей чертой. Они не могут привестись в действие при контакте рабочего тела только с одним тепловым. Их минимальное число должно быть равным двум.
Определение 2
Тепловой резервуар, обладающий более высоким значением температуры, носит название нагревателя, а с более низким – холодильника.
Рабочее тело при совершении кругового процесса получает от нагревателя некоторую теплоту Q1>0 и теряет, отдавая холодильнику, количество теплоты Q2<0. Для полного полученного рабочим телом за цикл количества теплоты Q справедливо следующее выражение:
Q=Q1+Q2=Q1-Q2.
Совершая цикл, рабочее тело приходит в свое первоначальное состояние, из чего можно сделать вывод, что изменение его внутренней энергии равняется ΔU=0. Основываясь на первом законе термодинамики, запишем:
∆U=Q-A=0.
Из этого следует:
A=Q=Q1-Q2.
Работа A, которую рабочее тело совершает за цикл, эквивалентна полученному за этот же цикл количеству теплоты Q.
Определение 3
Коэффициентом полезного действия или же КПД η теплового двигателя называют отношение работы A к полученному рабочим телом за цикл от нагревателя количеству теплоты Q1, то есть:
η=AQ1=Q1-Q2Q1.
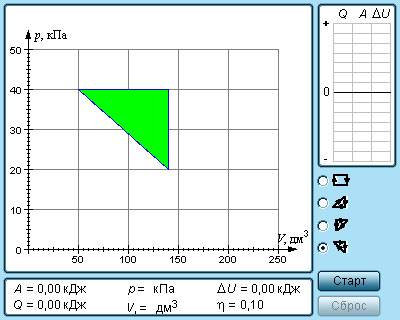
Рисунок 3.11.2. Модель термодинамических циклов.
Коэффициент полезного действия теплового двигателя демонстрирует, какая доля тепловой энергии, которую получило рабочее тело от нагревателя, преобразовалась в полезную работу. Оставшаяся часть (1–η) была без пользы передана холодильнику. Коэффициент полезного действия тепловой машины не может быть больше единицы η<1. На рисунке 3.11.3 проиллюстрирована энергетическая схема тепловой машины.
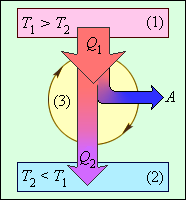
Рисунок 3.11.3. Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q1>0, A>0, Q2<0; T1>T2.
Виды тепловых двигателей
В технике свое применение находят двигатели, использующие круговые процессы. Рисунок 3.11.3 демонстрирует нам циклы, применяемые в бензиновом карбюраторном и в дизельном двигателях. Они оба в качестве рабочего тела используют смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания включает в себя две изохоры (1–2, 3–4) и две адиабаты (2–3, 4–1), дизельного двигателя -две адиабаты (1–2, 3–4), одну изобару (2–3) и одну изохору (4–1). Реальный КПД (коэффициент полезного действия) у карбюраторного двигателя составляет около 30 %, у дизельного двигателя – приблизительно 40 %.
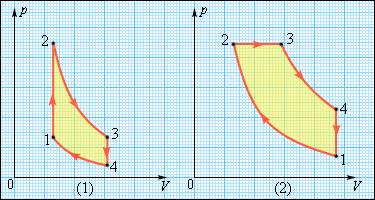
Рисунок 3.11.4. Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2).
Цикл Карно
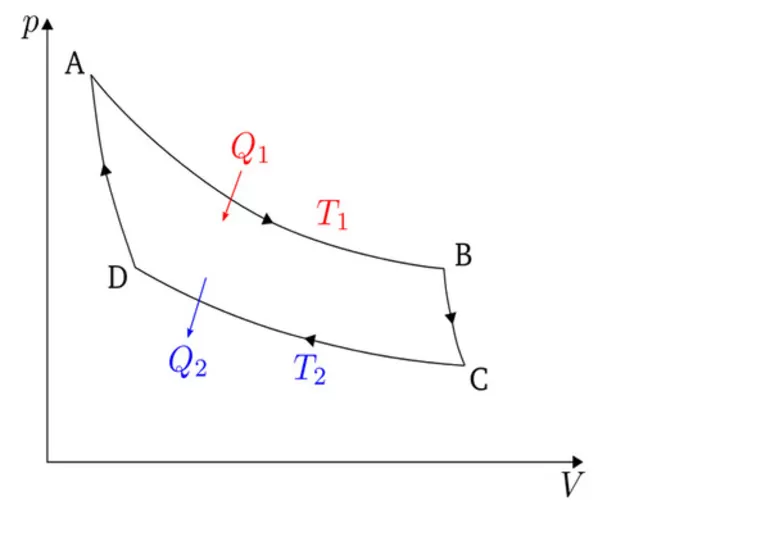
Круговой процесс, изображенный на рисунке 3.11.5, состоящий из двух изотерм и двух адиабат был назван циклом Карно в честь открывшего его в 1824 году французского инженера. Данное явление впоследствии оказало колоссальное влияние на развитие учения о тепловых процессах.
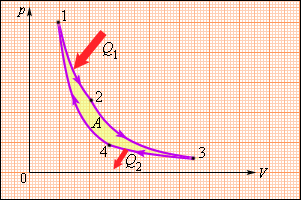
Рисунок 3.11.5. Цикл Карно.
Находящийся в цилиндре, под поршнем, газ совершает цикл Карно. На участке изотермы (1–2) он приводится в тепловой контакт с нагревателем, обладающим некоторой температурой T1. Газ изотермически расширяется, при этом к нему подводится эквивалентное совершенной работе A12количество теплоты Q1=A12. После этого на участке адиабаты (2–3) газ помещается в адиабатическую оболочку и продолжает процесс расширения при отсутствующем теплообмене. На данной части цикла газ совершает работу A23>0. Его температура при адиабатическом расширении снижается до величины T2. На идущем следующим участке изотермы (3–4) газ приводится в тепловой контакт с холодильником в условиях температуры T2<T1. Производится процесс изотермического сжатия. Газом совершается некоторая работа A34<0 и отдается тепло Q2<0, эквивалентное произведенной им работе A34. Его внутренняя энергия не претерпевает изменений. На последнем оставшемся участке адиабатического сжатия газ снова помещают в адиабатическую оболочку. При сжатии его температура вырастает до величины T1, также совершается работа A41<0. совершаемая газом за цикл полная работа A эквивалентна сумме работ на отдельных участках:
A=A12+A23+A34+A41.
На диаграмме (p, V) данная работа равняется площади цикла.
Процессы на любом из участков цикла Карно квазистатичны. Например, оба участка 1–2 и 3–4, относящихся к изотермическим, производятся при пренебрежительно малой разности температур рабочего тела, то есть газа, и теплового резервуара, будь то нагреватель или холодильник.
Исходя из первого закона термодинамики, можно заявить, что работа газа в условиях адиабатического расширения или сжатия эквивалентна падению значения ΔU его внутренней энергии. Для 1 моля газа верно следующее выражение:
A=-∆U=-CV(T2-T1),
в котором T1 и T2 представляют собой начальную и конечную температуры рабочего тела.
Из этого следует, что работы, совершаемые газом на двух адиабатических участках цикла Карно, противоположны по знакам и одинаковы по модулю:
A23=-A41.
Коэффициент полезного действия η цикла Карно может рассчитываться с помощью следующих соотношений:
η=AQ1=A12+A34Q12=Q1-Q2Q1=1-Q2Q1.
С. Карно выразил коэффициент полезного действия цикла через величины температур холодильника T2и нагревателя T1:
η=T1-T2T1=1-T2T1.
Цикл Карно примечателен тем, что ни на одном из его участков тела, обладающие различными температурами, не соприкасаются. Любое состояние рабочего тела в цикле является квазиравновесным, что означает его бесконечную близость к состоянию теплового равновесия с окружающими объектами, то есть тепловыми резервуарами или же термостатами. В цикле Карно исключен теплообмен в условиях конечной разности температур рабочего тела и окружающей среды (термостатов), если тепло имеет возможность переходить без совершения работы. По этой причине любые другие возможные круговые процессы проигрывают ему в эффективности при заданных температурах нагревателя и холодильника:
ηКарно=ηmax
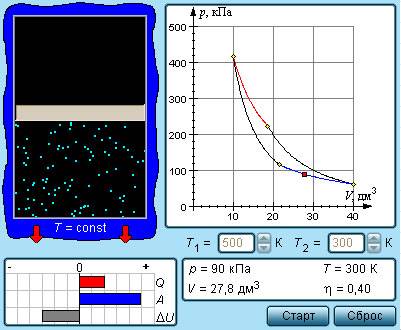
Рисунок 3.11.6. Модель цикла Карно.
Каждый участок цикла Карно и цикл в целом могут проходиться в обоих направлениях.
Определение 4
Обход цикла по часовой стрелке соответствует тепловому двигателю, в котором полученное рабочим телом тепло частично преобразуется в полезную работу. Обход против часовой стрелки соответствует холодильной машине, где некое количество теплоты отходит от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Именно поэтому идеальное устройство, работающее по циклу Карно, носит название обратимой тепловой машины.
В реально существующих холодильных машинах применяются разные циклические процессы. Любой холодильный цикл на диаграмме (p, V) обходятся против часовой стрелки. На рисунке 3.11.7 проиллюстрирована энергетическая схема холодильной машины.
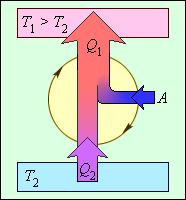
Рисунок 3.11.7. Энергетическая схема холодильной машины. Q1<0, A>0, Q2 > 0, T1>T2.
Работающее по холодильному циклу устройство может обладать двояким предназначением.
Определение 5
Если полезным эффектом является отбор некоторого количества тепла Q2 от охлаждаемых тел, к примеру, от продуктов в камере холодильника, то такое устройство является обычным холодильником.
Эффективность работы холодильника может быть охарактеризована следующим отношением:
βx=Q2A.
Таким образом, эффективность работы холодильника представляет собой количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. В условиях подобного определения βх может быть, как больше, так и меньше единицы. Для обращенного цикла Карно справедливо выражение:
βx=T2T1-T2.
Определение 6
В случае, когда полезным эффектом является передача некоего количества тепла
|Q1| нагреваемым телам, чьим примером может выступать воздух в помещении, то такое устройство называется тепловым насосом.
Эффективность βТ теплового насоса может быть определена с помощью отношения:
βт=Q1A.
То есть она может определяться количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует:
Q1>A.
Следовательно, βТ всегда больше единицы. Для обращенного цикла Карно справедливо следующее выражение:
βт=1η=T1T1-T2.
Цикл
Карно—
это обратимый круговой процесс, состоящий
из двух адиабатических и двух изотермических
процессов. В процессе Карно термодинамическая
система выполняет механическую работу
и обменивается теплотой с
двумя тепловыми резервуарами, имеющими
постоянные, но различающиеся температуры.
Резервуар с более высокой температурой
называется нагревателем, а с более
низкой температурой — холодильником.
КПД
для идеального газа—
Вычислим
КПД цикла Карно для идеального газа.
При изотермическом процессе внутренняя
энергия идеального газа остаётся
постоянной. Поэтому количество полученной
газом теплоты равно
работе ,
совершаемой газом при переходе из
состояния 1 в состояние 2.(рис 2)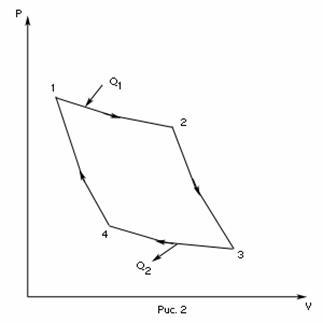
Эта работа равна
,
где –
масса идеального газа в тепловой машине.
Количество
отдаваемой холодильнику теплоты равно
работе ,
затраченной на сжатие газа при переходе
его из состояния 3 в состояние 4. Эта
работа равна
.
Для
того чтобы цикл был замкнутым, состояние
1 и 4 должны лежать на одной и той же
адиабате. Отсюда вытекает условие
.
Аналогично
для состояний 2 и 3 должно вытекать
условие
.
Разделив
одно соотношение на другое, приходим к
условию замкнутости цикла
.
Теперь
подставляя и в
выражение для КПД, получим
.
(2)
В
результате получим формулу для КПД
цикла Карно:
26. Барометрическая формула. Распределение Больцмана.
При
выводе основного уравнения
молекулярно-кинетической теории газов
и максвелловского распределения молекул
по скоростям делалось предположение,
что внешние силы не действуют на молекулы
газа, поэтому молекулы равномерно
распределены по объему. Но молекулы
любого газа находятся в потенциальном
поле тяготения Земли. Сила тяжести, с
одной стороны, и тепловое движение
молекул — с другой, приводят газ к
некоторому стационарному состоянию,
при котором давление газа с высотой
уменьшается.
Выведем
закон изменения давления с высотой,
предполагая при этом, что масса всех
молекул одинакова, поле тяготения
однородно и температура постоянна.
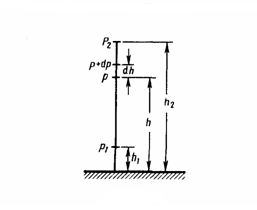
Рис.1
Если
атмосферное давление на высоте h равно
р (рис. 1), то на высоте h+dh оно равно p+dp
(при dh>0 dp<0, так как давление с высотой
уменьшается). Разность давлений р и p+dp
равна весу газа, заключенного в объеме
цилиндра высотой dh с основанием площадью
1 м2:
где
ρ — плотность газа на высоте h (dh настолько
мало, что при изменении высоты в этом
интервале плотность газа можно считать
постоянной). Значит,
(1)
Зная
уравнение состояния идеального газа
pV=(m/M) RT (m — масса газа, М — молярная масса
газа), находим, что
Подставив
это выражение в (1), получим
или
С
изменением высоты от h1 до
h2 давление
изменяется от р1 до
р2 (рис.
67), т. е.
или
(2)
Выражение
(2) называется барометрической
формулой.
Она позволяет вычислить атмосферное
давление в зависимости от высоты или,
измеряя давление, найти высоту: Так как
высоты считаются относительно уровня
моря, где давление считается нормальным,
то выражение (2) может быть представлено
в виде
(3)
где
р — давление на высоте h.
Прибор
для определения высоты над земной
поверхностью называется высотомером (или альтиметром).
Его работа основана на применении
формулы (3). Из этой формулы следует, что
чем тяжелее газ, тем давление с высотой
убывает тем быстрее.
Барометрическую
формулу (3) можно преобразовать, если
воспользоваться формулой p=nkT:
где
n – концентрация молекул на высоте h,
n0 –
то же, на высоте h=0. Так как M=m0NA (NA –
постоянная Авогадро, m0 –
масса одной молекулы), a R=kNA,
то
(4)
где
m0gh=P
— потенциальная энергия молекулы в
поле тяготения, т. е.
(5)
Выражение
(5) называется распределением
Больцмана для
внешнего потенциального поля. Из него
видно, что при постоянной температуре
плотность газа больше там, где меньше
потенциальная энергия его молекул.
Если
частицы находятся в состоянии хаотического
теплового движения и имеют одинаковую
массу и , то распределение Больцмана
(5) применимо в любом внешнем потенциальном
поле, а не только в поле сил тяжести.
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Краткая биография
Николя Леонард Сади Карно, сын высокопоставленного военачальника Лазаря Николая Маргарита Карно, родился в Париже в 1796 году. Его отец ушёл из армии в 1807 году, чтобы обучить Николаса и его брата Ипполита — оба получили широкое домашнее образование, включающее:
- науку;
- искусство;
- иностранные языки;
- музыку.
В 1812 году 16-летний Николас Карно был принят в Высшую политехническую школу в Париже. Его учителями были Джозеф Луи Гей-Люссак, Симеон Дени Пуассон и Андре-Мари Ампер, а сокурсниками — будущие учёные Клод-Луи Навье и Гаспар-Гюстав Кориолис. Во время учёбы в школе Карно проявил особый интерес к теории газов и решению задач промышленной инженерии. После окончания университета он поступил во французскую армию в качестве военного инженера и прослужил до 1814 года.
Освободившись от ограничений военной жизни, Карно начал широкий спектр исследований, которые продолжались, несмотря на многочисленные перерывы, до само́й смерти. В дополнение к частным занятиям он посещал курсы:
- в Сорбонне;
- Коллеж де Франс.
- в Школе шахт;
- в Консерватории искусств.
В последней он стал другом Николаса Клемента, который преподавал курс прикладной химии, а затем занимался важными исследованиями паровых двигателей и теории газов.
Одним из особых интересов Карно было промышленное развитие, которое он изучал во всех его аспектах. Он часто посещал фабрики и мастерские, читал новейшие теории политической экономии и оставлял в своих заметках подробные предложения по таким актуальным проблемам, как налоговая реформа. Помимо этого, его деятельность и способности охватили математику и изобразительное искусство.
В 1821 году Карно прервал учёбу, чтобы провести несколько недель со своим отцом и братом в Магдебурге. По-видимому, именно после этого визита он снова в Париже начал концентрироваться на проблемах парового двигателя. 12 июня 1824 года была опубликована его книга «Отражение в чистоте и весе».
После публикации Карно продолжил исследования, выводы из которых сохранились в его рукописных заметках. Однако реорганизация корпуса Генерального штаба вынудила Карно вернуться на службу в 1827 году в звании капитана. После менее чем годовой работы в качестве военного инженера Карно ушёл в отставку навсегда и вернулся в Париж. Он снова сосредоточил своё внимание на проблемах конструкции двигателя и теории тепла.
В 1831 году Карно начал исследовать физические свойства газов и паров, особенно связь между температурой и давлением. Однако в июне 1832 года он заболел скарлатиной. За этим последовала «мозговая лихорадка», которая настолько подорвала его хрупкое здоровье, что 24 августа 1832 года он стал жертвой эпидемии холеры и умер в течение дня, в возрасте 36 лет. Согласно обычаю, его личные вещи, включая почти все его бумаги, были сожжены.
Работы учёного
Самая ранняя из основных рукописей написана, вероятно, в 1823 году и озаглавлена «Поиск формулы для представления движущей силы водяного пара». Как видно из названия, это была попытка найти математическое выражение для движущей силы, производимой паром. Явно стремясь найти общее решение, охватывающее все типы паровых двигателей, Карно сократил их работу до трёх основных этапов:
- изотермическое расширение при подаче пара в цилиндр;
- адиабатическое расширение;
- изотермическое сжатие в конденсаторе.
Эссе как по методам, так и по целям похоже на многие статьи, опубликованные между 1818 и 1824 годами такими учёными, как Хашетт, Навье, Пети и Комбес. Работа Карно, однако, отличается своим тщательным, чётким анализом используемых единиц и концепций и тем, что он использует как адиабатическую рабочую стадию, так и изотермическую стадию. Отточенный характер, в отличие от его грубых заметок, делало её предназначенной для публикации, хотя она оставалась неизвестной в рукописи до 1966 года.
«Рефлексионы» (единственное произведение, опубликованное Карно за всю его жизнь) появилось в 1824 году как скромное эссе из 118 страниц. После краткого обзора промышленного, политического и экономического значения парового двигателя Карно поднял две проблемы, которые, по его мнению, помешали дальнейшему развитию как полезности, так и теории паровых двигателей:
- Существует ли установленный предел для движущей силы тепла и, следовательно, для улучшения паровых двигателей?
- Есть ли агенты предпочтительнее пара в производстве этой движущей силы?
Обе проблемы были своевременными и, хотя французские инженеры исследовали их в течение десятилетия, не было принято общепринятых решений. В отсутствии чёткой концепции эффективности предлагаемые конструкции паровых двигателей оценивались в основном по практичности, безопасности и экономии топлива.
Некоторые инженеры считали воздух, углекислоту и спирт лучшим рабочим веществом, чем пар. Обычным подходом к этим проблемам было либо эмпирическое исследование расхода топлива и выходной мощности отдельных двигателей, либо применение математической теории газов к абстрактным операциям конкретного типа двигателя. В своём выборе проблем Карно был твёрд в этой инженерской традиции, однако его метод был радикально новым и являлся сутью его вклада в науку о тепле.
Предыдущая работа над паровыми машинами, как видел Карно, провалилась из-за отсутствия достаточно общей теории, применимой ко всем тепловым двигателям и основанной на установленных принципах. В качестве основы своего исследования Карно тщательно изложил три предпосылки. Первой была невозможность вечного движения — принцип, который долгое время предполагался в механике. В своей второй предпосылке Карно использовал калорийную теорию тепла, которая, несмотря на некоторую оппозицию, была принятой и самой развитой, доступной теорией тепла.
Принципы работы цикла Карно
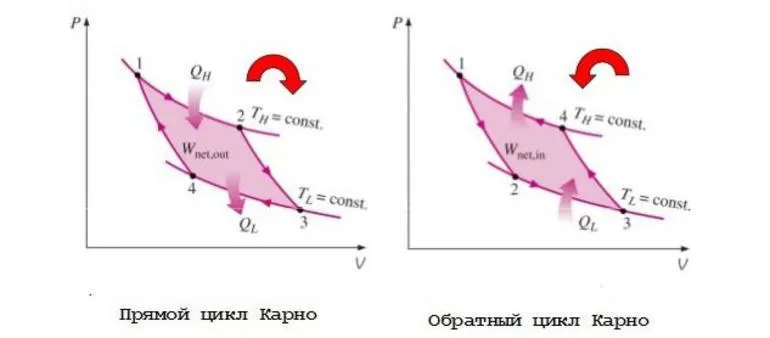
Этот теоретический идеальный круговой термодинамический цикл был предложен французским физиком Сади Карно в 1824 году. Он обеспечивал максимально возможный предел эффективности для любого классического термодинамического двигателя во время преобразования тепла в работу или, наоборот, эффективность системы охлаждения при создании разницы температур при приложении работы к системе. Фактический термодинамический цикл является теоретической конструкцией.
Каждая термодинамическая система существует в определённом состоянии. Когда система проходит через ряд различных явлений и, наконец, возвращается в исходное состояние, говорят, что произошёл термодинамический цикл. В процессе прохождения этого цикла система может выполнять работу, например, перемещая поршень, тем самым действуя, как тепловой двигатель.
Из каких процессов состоит Цикл Карно при работе в качестве теплового двигателя:
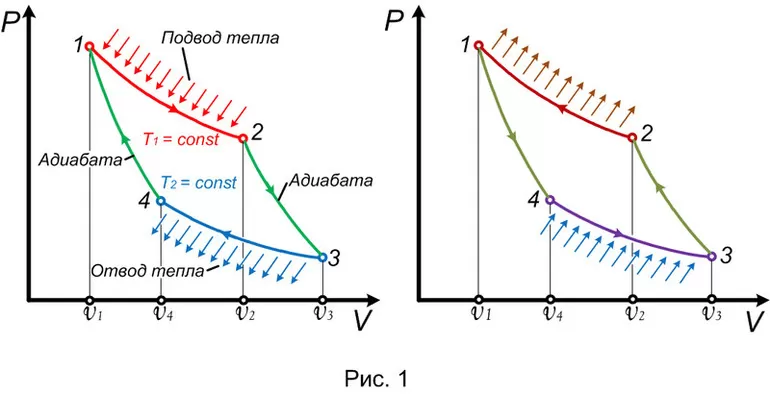
- Изотермическое расширение. Тепло передаётся обратимо из высокотемпературного резервуара при постоянной температуре T H (изотермическое добавление или поглощение тепла). На этом этапе газу позволяют расширяться, выполняя работу над окружающей средой, толкая поршень. Хотя давление падает, температура газа не изменяется во время процесса, поскольку он находится в тепловом контакте с горячим резервуаром в момент времени T h и, следовательно, расширение является изотермическим.
- Изоэнтропическое (обратимое адиабатическое) расширение газа. На этом этапе газ теплоизолирован как от горячего, так и от холодного резервуаров. Таким образом, они не получают и не теряют тепло. Газ продолжает расширяться за счёт снижения давления, выполнения работы на окружающую среду и потери количества внутренней энергии, равного проделанной работе. Расширение газа без подвода тепла приводит к его охлаждению до «холодной» температуры. Энтропия остаётся неизменной.
- Изотермическая компрессия. Тепло передаётся обратимо в низкотемпературный резервуар при постоянной температуре (изотермический отвод тепла). Теперь газ в двигателе находится в тепловом контакте с холодным резервуаром. Окружение работает на газе, толкая поршень вниз, в результате чего количество тепловой энергии Q 2 покидает систему в низкотемпературный резервуар, а энтропия системы уменьшается.
- Адиабатическое обратимое сжатие. Ещё раз газ в двигателе теплоизолирован от горячего и холодного резервуаров и предполагается, что двигатель не имеет трения и, следовательно, обратим. На этом этапе окружающая среда воздействует на газ, продвигая поршень вниз, увеличивая его внутреннюю энергию, сжимая и заставляя температуру подниматься обратно, но энтропия остаётся неизменной. В этот момент газ находится в том же состоянии, что и в начале шага 1.
Система, проходящая через этот цикл, называется тепловым двигателем Карно, хотя такой «идеальный» двигатель является лишь теоретической конструкцией и не может быть построен на практике. Тем не менее был разработан и запущен микроскопический тепловой двигатель.
По существу, есть два «тепловых резервуара», образующих часть теплового двигателя при температурах T h и T c (соответственно, горячий и холодный). Они обладают такой большой теплоёмкостью, что их температуры практически не зависят от одного цикла. Поскольку цикл теоретически обратим, энтропия в течение цикла не возникает, но сохраняется.
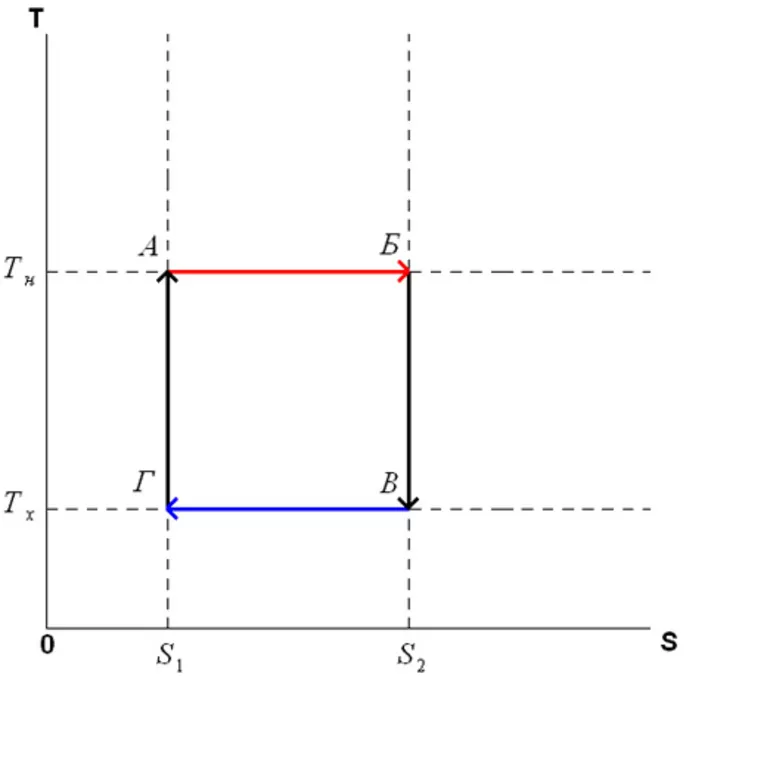
Во время цикла произвольное количество энтропии S извлекается из горячего резервуара (нагревателя) и осаждается в холодном резервуаре. Поскольку в обоих резервуарах изменения объёма не происходит, они не работают, и в течение цикла количество энергии T h ΔS извлекается из горячего резервуара, а меньшее количество энергии T c ΔS откладывается в холодном резервуаре. Разница в двух энергиях (T h -T c) ΔS равна работе, проделанной двигателем.
Поведение двигателя или холодильника Карно лучше всего понять с помощью диаграммы, в которой координатами являются температура и энтропия. Термодинамическое состояние определяется точкой на графике с энтропией (S) в качестве горизонтальной оси и температуры (T) в качестве вертикальной оси. Для простой замкнутой системы любая точка на графике будет представлять конкретное состояние системы. Термодинамический процесс будет состоять из кривой, соединяющей начальное состояние (A) и конечное состояние (B), и представляющей собой количество тепловой энергии, передаваемой в процессе.
Если процесс движется к большей энтропии, площадь под кривой будет количеством тепла, поглощённого системой. Когда процесс движется к меньшей энтропии, это будет количество отводимого тепла. Для любого циклического процесса есть верхняя часть цикла и нижняя часть. Для цикла по часовой стрелке область под верхней частью будет тепловой энергией, поглощённой в течение цикла, тогда как область под нижней частью будет тепловой энергией, удалённой во время цикла.
Площадь внутри цикла будет тогда разницей между ними, но поскольку внутренняя энергия системы должна вернуться к своему первоначальному значению, эта разница должна быть объёмом работы, которую должна совершать системой за цикл.
Перевёрнутый цикл
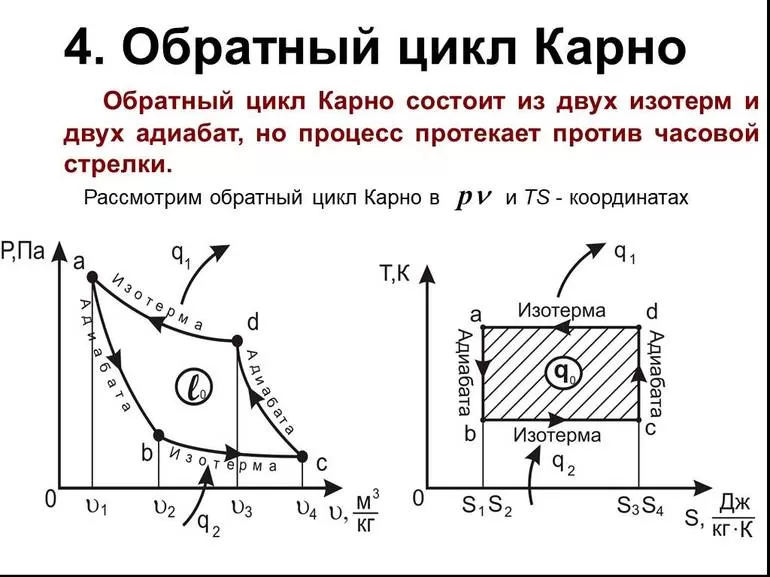
Описанный цикл теплового двигателя является полностью обратным циклом Карно. То есть все процессы, из которых он состоит, могут быть обращены вспять, и в этом случае цикл становится холодильным циклом Карно.
На этот раз цикл остаётся точно таким же, за исключением того, что направления любых тепловых и рабочих взаимодействий меняются местами. Тепло поглощается из низкотемпературного резервуара, отбрасывается в высокотемпературный резервуар, и для этого требуется работа. Диаграмма P-V обращённого цикла такая же, как и для цикла Карно, за исключением того, что направления процессов меняются местами.
Если же в цикле возникает передача теплоты при наличии разности температур, а такими являются все технические реализации термодинамических циклов, то цикл становится необратимым. КПД такого цикла будет всегда меньше, чем КПД цикла Карно.
Теорема Карно
Эта теорема является формальным утверждением этого факта: ни один двигатель, работающий между двумя тепловыми резервуарами, не может быть более эффективным, чем двигатель Карно, работающий между этими же резервуарами.
Следствие из теоремы Карно гласит: все реверсивные двигатели, работающие между одними и теми же тепловыми резервуарами, одинаково эффективны. Теоретический максимальный КПД теплового двигателя равён разнице в температуре между горячим и холодным резервуаром, делённой на абсолютную температуру горячего резервуара.
Исходя из этого, становится очевидным интересный факт: понижение температуры холодного резервуара будет иметь большее влияние на потолочную эффективность теплового двигателя, чем повышение температуры горячего резервуара на ту же величину. В реальном мире это труднодостижимо, так как холодный резервуар часто имеет существующую температуру окружающей среды.
Другими словами, максимальная эффективность достигается тогда, когда в цикле не создаётся новая энтропия, что было бы в случае, если, например, трение привело к рассеиванию работы в тепло. В противном случае, поскольку энтропия является функцией состояния, требуемый сброс тепла в окружающую среду для удаления избыточной энтропии приводит к (минимальному) снижению эффективности.
В мезоскопических тепловых двигателях работа за цикл обычно колеблется из-за теплового шума. Если цикл выполняется квазистатически, флуктуации исчезают даже на мезомасштабах. Но если цикл выполняется быстрее, чем время релаксации рабочего тела, колебания работы неизбежны. Тем не менее когда учтены рабочие и тепловые колебания, существует точное равенство, которое связывает экспоненциальное среднее значение работы, выполненной любым тепловым двигателем, и теплопередачу от горячей тепловой ёмкости.
Карно понимал, что в действительности невозможно создать термодинамический обратимый двигатель, поэтому реальные тепловые двигатели менее эффективны. Кроме того, реальные двигатели, работающие в этом цикле, встречаются редко. Но хотя прямой цикл французского учёного является идеализацией, его выражение эффективности всё ещё полезно для дальнейших исследований.
Примером обратимого цикла также является идеальный цикл Стирлинга. Существует и другие идеальные циклы, в которых коэффициент полезного действия определяется по той же формуле, что и для циклов Карно и Стирлинга, например, цикл Эрикссона.